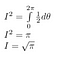Lord Kelvin skrev om dette integral: “En matematiker er en, for hvem det er lige så indlysende, som det er lige så indlysende for dig, at to gange to giver fire.”

Nyd det 😉

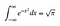
OK, så jeg går ud fra, at du kender noget grundlæggende integration og differentiering. Det følgende vil tilføje noget intuition til smarte tricks, som kommer senere. Du skal ikke bekymre dig, hvis noget af det er lidt forvirrende, men prøv bare at få en fornemmelse for, hvad der sker.

Strategien her vil være at foretage en smart substitution. Men vi vil foretage en substitution i to variabler. Du kan visualisere det aktuelle problem som en beregning af arealet under en kurve

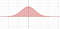
Men vi vil vise, at problemet kan vendes til et problem om at beregne et volumen.

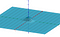
For at beregne rumfanget bruger vi en lidt anden variabelskifteformel end den, man bruger i normale integraler. Vi vil bruge polære koordinater. Dette udtrykker x- og y-koordinaterne i form af deres radius og deres vinkel. Geogebra har en fin interaktiv måde at se det på her

Så vil vi bruge den magiske ændring af basisformlen for polarkoordinater.

Ved beregning af arealet under kurven havde vi elementet ‘dx’, som repræsenterer en lille afstand langs x-aksen. Når vi beregner et rumfang, har vi dx dy, som svarer til et lille rektangel med sidelængderne dx og dy. Vi bruger så disse baser til at skabe en række kasser, som estimerer volumenet. Dette er nemmest at se med visualiseringen nedenfor. Integralet er grænsen af disse tilnærmelser.

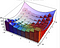
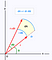
Når vi i stedet bruger det polære koordinatsystem, har vi et lidt anderledes arealelement nedenunder. Nedenfor er dA arealelementet. Med små ændringer i vinklen og radius kan dette arealelement tilnærmes stadig bedre ved et rektangel med sidelængderne dr og r*dtheta henholdsvis. Hvis du er fortrolig med noget geometri, så tilnærmes sin(theta) for små theta meget godt med theta, og du kan så bevise resultatet nedenfor.

Løsning af integralet

Først giver vi et navn til vores integral. Vi kalder det I.

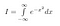
Bemærk, at x blot er en ‘dummy-variabel’. Området eksisterer, uanset hvilket variabelnavn vi bruger. Så vi kan også skrive følgende to ligninger

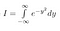
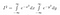
Nu, da I bare er en konstant, omend en vi ikke kender værdien af endnu, kan vi bruge vores normale regler for at bringe en konstant inden for et integral

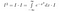
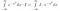
Så langt har vi ikke gjort meget substantielt. Nu tænker vi grundigt over, hvad integralet betyder. Vi tager integraler af funktioner. Hvis to funktioner tager den samme værdi overalt, er de ens og har samme areal. Med det i baghovedet kan vi lave følgende manipulationer, hvis vi ser I*exp(-x²) som en funktion af x, dvs. noget der tager værdier af x ind som input, og giver et tal som output.

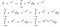
Okay, det var meget at tage ind. I den første linje har vi bare omskrevet I i sin integralform med et andet variabelnavn. I den anden linje, hvor vi behandlede I*exp(-x²) som en funktion, indså vi, at vi kan bringe exp(-x²) ind i dy-integralet, og dette ville stadig give den samme udgangsværdi for enhver indgangsværdi af x. Til sidst brugte vi reglerne for eksponering.

Så har vi nu

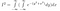
Næste kommer den dræbende indsigt. Ovenfor har vi rodet rundt med variabelnavne og hvordan man repræsenterer en funktion. Nu skifter vi perspektiv: Dette udtryk repræsenterer også integralet af exp(-(y²+x²)) over hele 2D-planet, med arealelementet dA = dx dy. Dvs. dx dy er et lille rektangel på et plan, og exp(-(y²+x²)) er højden over dette rektangel.

Næst bruger vi polarkoordinaternes indsigt fra tidligere

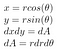
Som sin² + cos² = 1, efter at vi har sat det hele ind, får vi

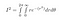
r spænder fra 0 til uendelig og theta spænder fra 0 til 2*pi, fordi dette dækker hele 2D-planet: ethvert punkt har en radius mindre end uendelig og en vinkel mellem 0 og 2pi radianer.

Vi kan evaluere det indre integral ved hjælp af kædereglen

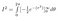
Og, ind i det forjættede land befinder vi os nu: