Når lys reflekteres eller transmitteres fra en materialestruktur, sker der en ændring i polarisationen. Ellipsometri måler denne reaktion, som afhænger af de optiske egenskaber og tykkelsen af de enkelte materialer. Ellipsometri anvendes primært til at bestemme optiske konstanter og filmtykkelse, men også til at karakterisere sammensætning, krystallinitet, ruhed, dopingkoncentration og andre materialeegenskaber, der er forbundet med en ændring i den optiske respons.

Anvendelsesområder er grundforskning inden for fysiske videnskaber, halvleder- og datalagringsløsninger, fladskærme, kommunikation, biosensorer og optiske belægningsindustrier. Ellipsometri har også fleksibilitet til at måle de fleste materialetyper: dielektriske stoffer, halvledere, metaller, superledere, organiske stoffer, biologiske belægninger og kompositter.

Definition af polariseret lys

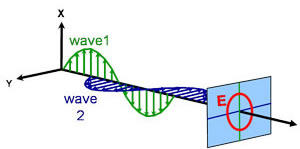
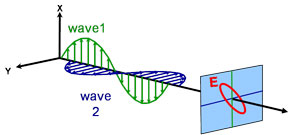
Lys kan beskrives som en elektromagnetisk bølge, der bevæger sig gennem rummet. Den måde, hvorpå en elektromagnetisk bølges felt opfører sig i forhold til rum og tid, betegnes som polarisering. Lys anses for at være upolariseret, når dets orientering og fase er helt vilkårlige. Ellipsometri måler imidlertid polariseret lys – et elektrisk felt, der følger en bestemt bane og har en bestemt form i ethvert givet punkt. En elektromagnetisk bølge, der bevæger sig i z-retningen, kan beskrives ved hjælp af dens x- og y-komponenter, fordi dens elektriske felt altid er ortogonalt til udbredelsesretningen. Når to ortogonale lysbølger er i fase, er det resulterende lys lineært polariseret. Dets retning bestemmes af de relative amplituder. Lyset anses for at være cirkulært polariseret, hvis de ortogonale bølger er 90° ude af fase og har samme amplitude. Den mest almindelige polarisering er elliptisk og kombinerer ortogonale bølger med vilkårlig amplitude og fase. Det er herfra, at ellipsometri har sit navn.

Differente typer af polarisering:

Linær

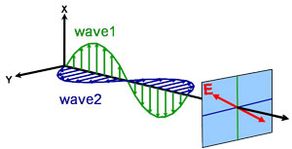
Cirkulær

Elliptisk

Optiske egenskaber

De optiske egenskaber, som bestemmer, hvordan lys interagerer med et materiale, beskrives ved to værdier. De repræsenteres generelt som et komplekst tal. Det komplekse brydningsindeks (ñ) består af indekset (n) og en extinktionskoefficient (k):

De optiske egenskaber kan også beskrives som en kompleks dielektrisk funktion:

med følgende sammenhæng mellem konventionerne:

Indekset viser lysets fasehastighed, når det bevæger sig i et materiale, sammenlignet med lysets hastighed, når det bevæger sig i vakuum, c:

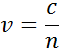
Når det kommer ind i et materiale med et højere indeks, bliver lyset langsommere. Da lysbølgernes frekvens ikke ændres, bliver bølgelængden kortere. Tabet af bølgeenergi til materialet beskrives af extinktionskoefficienten, som er relateret til absorptionskoefficienten på følgende måde:

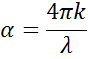
I henhold til Beers lov mister lyset intensitet i et absorberende materiale. Extinktionskoefficienten viser, hvor hurtigt lyset forsvinder i et materiale.

Figur 4 viser en lysbølge, der bevæger sig gennem to forskellige materialer med varierende egenskaber, inden den vender tilbage til omgivelserne.

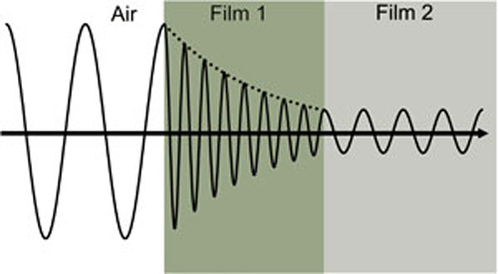
Figur 4: Lysbølge, der bevæger sig fra luft ind i absorberende Film 1 og derefter i transparent Film 2. Fasehastigheden og bølgelængden ændres i begge materialer afhængigt af brydningsindekset (Film 1: n=4, Film 2: n=2).

Bølgelængden bestemmer de optiske konstanter. Figur 5 viser de optiske konstanter for TiO2 fra UV til IR. På grund af forskellige processer, der trækker energi fra lysbølgen, forekommer absorption (k>0) i både UV og IR. IR-absorption er normalt forårsaget af molekyl- eller fononvibrationer eller frie bærere. UV-absorption finder generelt sted på grund af elektroniske overgange, hvor lysenergi exciterer elektroner til forhøjede tilstande. Figur 5 viser, at hypotetiske eller reelle optiske konstanter ikke er uafhængige, men matematisk forbundet gennem Kramers-Kronig-relationer.

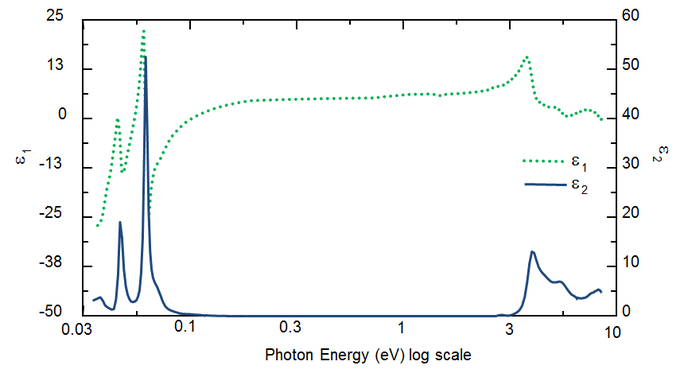
Figur 5: Kompleks dielektrisk funktion for TiO2-film med bølgelængder fra IR (små eV) til UV (høje eV).

Lys- og materialeinteraktion

Når lys interagerer med et materiale, fører dette til grænsebetingelser ved grænsefladen. Under dette skal Maxwells ligninger altid forblive opfyldt. Nedenstående figur viser, hvordan indfaldende lys reflekteres og brydes ved grænsefladen. Vinklen mellem den indfaldende stråle og prøvenormalen (θi) vil være lig med den reflekterede vinkel (θr). Lys, der trænger ind i et materiale, brydes i en vinkel θt, der er givet ved:

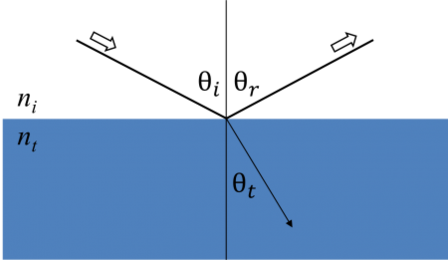
Figur 6: Lyset reflekteres og brydes i henhold til Snells lov.

På enhver grænseflade reflekteres en del af lyset, mens resten transmitteres i den brydningsvinkel. Afhængigt af randbetingelserne gælder forskellige løsninger for elektriske felter parallelt og vinkelret på prøveoverfladen. Lyset kan således opdeles i ortogonale komponenter i forhold til det indfaldende plan (p- og s-polariseret). Begge komponenter kan beregnes separat. Sådan beskrev Fresnel mængden af lys, der reflekteres og transmitteres ved en grænseflade mellem materialer:

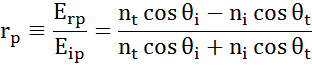
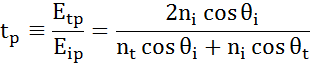
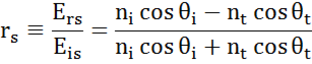
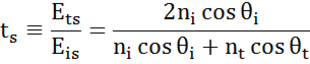
Multiple grænseflader med passende Fresnel-reflektions- og transmissionskoefficienter forekommer ved tynde film og flerlagsstrukturer. For at kunne definere den reflekterede eller transmitterede stråle korrekt skal den relative fase for hver enkelt lyskomponent følges. Filmens fasetykkelse bestemmes således på følgende måde:

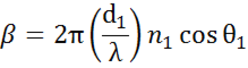
Når flere lysbølger overlejres, opstår der interferens, som afhænger af den relative fase af hver enkelt lysbølge. Nedenstående figur viser kombinationen af lysbølger i den reflekterede stråle og deres tilsvarende Fresnel-beregninger.

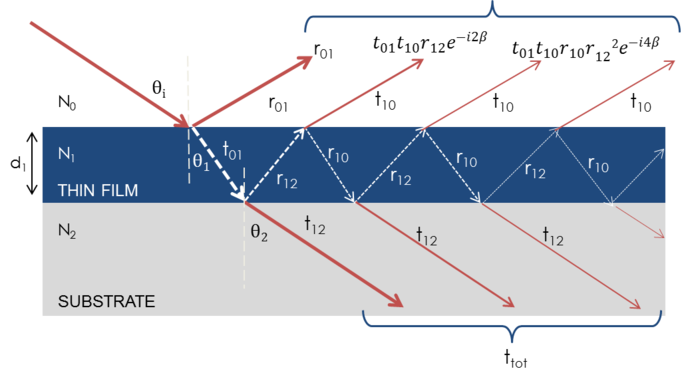
Figur 7: Lyset reflekteres og brydes ved hver enkelt grænseflade, hvilket fører til flere stråler i en tynd film. Stråleinterferens afhænger af den relative fase og amplitude af de elektriske felter. Strålreaktionen kan beregnes med Fresnel-reflektions- og transmissionskoefficienter.

Målinger

Ellipsometri måler hovedsagelig, hvordan p- og s-komponenter reagerer i forhold til hinanden under refleksion eller transmission. Derfor er en referencestråle altid en del af forsøget. En kendt polarisering reflekteres eller transmitteres fra prøven, og udgangspolariseringen måles. Polarisationsændringen er ellipsometri-målingen:

Figur 6 viser en typisk ellipsometri-måling af en prøve. Det lineært indfaldende lys har både p- og s- komponenter. Det reflekterede lys viser både amplitude- og faseændringer for både p- og s- polariseret lys. Disse ændringer måles ved ellipsometri.

For at indsamle ellipsometri-data er der brug for følgende: lyskilde, polarisationsgenerator, prøve, polarisationsanalysator og detektor. Både polarisationsgenerator og analysator består af optiske dele, der manipulerer polarisationen: kompensatorer, polarisatorer og fasemodulatorer. Typiske ellipsometerkonfigurationer omfatter en roterende analysator (RAE), en roterende polarisator (RPE), en roterende kompensator (RCE) og en fasemodulator (PME). Figuren nedenfor viser en RAE-konfiguration.

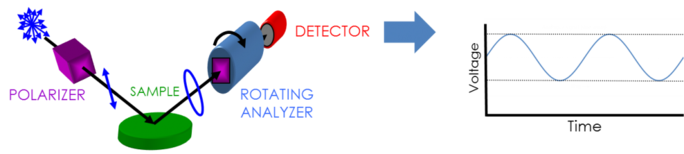
Upolariseret lys produceres af en lyskilde og sendes derefter gennem en polarisator. Polarisatoren er indstillet til kun at lade lys med en bestemt elektrisk feltorientering passere. Da polarisatorens akse er justeret mellem p- og s-planet, når begge dele frem til prøveoverfladen. Det nu lineært polariserede lys reflekteres fra prøveoverfladen og bliver således elliptisk polariseret, hvorefter det sendes gennem en kontinuerligt roterende polarisator (“analysator”). Den mængde lys, der får lov til at passere, afhænger af polarisatorens orientering i forhold til prøvens ellipse af det elektriske felt. For at bestemme den reflekterede polarisering omdannes lyset til et elektronisk signal i detektoren. Sammenligning af disse data med den etablerede indgangspolarisering giver oplysninger om den ændring, der er forårsaget af prøvens refleksion: den ellipsometriske måling af Psi og Delta.

Dataanalyse

Ellipsometri anvendes til at definere materialeskinnetykkelse eller optiske konstanter ved at måle ændringerne i lysets polarisering. “Pseudo”-optiske konstanter fra ellipsometri-målingerne kan udledes ved at vende de data, der er bestemt for en enkelt refleksion, om. Dette er nyttigt for bulkmateriale.

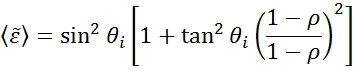
Overstående ligning tæller ikke med eventuelle overfladelag. Ikke desto mindre er der normalt et overfladeoxid eller en ruhed i bulkmaterialer. En direkte inversion vil inkludere disse data som en del af de optiske bulkkonstanter. Se fig. 10 for en oversigt over en typisk dataanalyseproces, der anvendes ved ellipsometriske målinger. Da der ikke kan skrives en nøjagtig ligning, er det nødvendigt at foretage en regressionsanalyse. Svaret er ofte overbestemt med kun få ubekendte og hundredvis af eksperimentelle datapunkter. En regressionsanalyse gør det muligt at inddrage alle de målte data, når løsningen skal bestemmes.

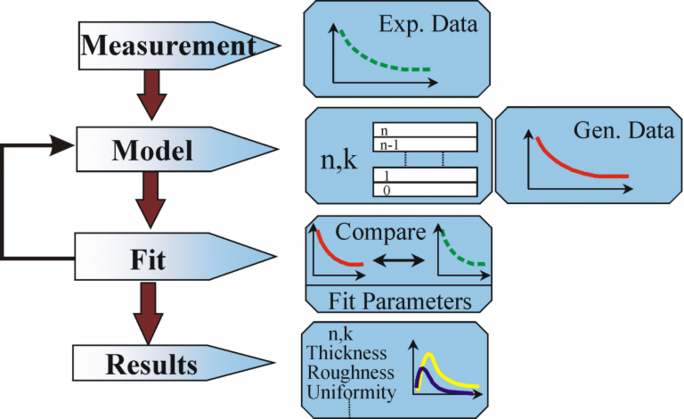
Figur 10: Flowdiagram for ellipsometridataanalyse.

Der anvendes følgende procedure til dataanalyse: Prøven måles, og der laves en model af prøven. Ved hjælp af denne model beregnes de antagne resultater fra Fresnel-ligningerne, som beskriver tykkelsen og de optiske konstanter for hvert materiale. Der foretages en vurdering af den foreløbige beregning, hvis disse værdier er ukendte. De beregnede værdier sammenlignes med de eksperimentelle data. For at opnå en bedre overensstemmelse mellem de eksperimentelle data og beregningsdataene kan ukendte materialedata varieres. De eksperimentelle datapunkter bør dog altid være større end de ukendte parametre. F.eks. kan der maksimalt bestemmes to materialeegenskaber med et ellipsometer med én bølgelængde, da det giver præcis to datapunkter: Ψ, Δ (Psi og Delta). Regression anvendes til at finde den bedste overensstemmelse mellem model og eksperiment. Forskellen mellem datakurverne kvantificeres ved hjælp af en estimator som f.eks. den gennemsnitlige kvadrerede fejl (MSE). Ukendte egenskaber varieres, indtil den mindste MSE er nået. Det betyder, at den laveste MSE svarer til det bedste svar.

Se nedenstående figur for MSE-kurven i forhold til filmtykkelsen for en transparent film på silicium. Den laveste MSE-værdi forekommer ved en tykkelse på 749 nm på trods af en række lokale minima. Den korrekte filmtykkelse er således også 749 nm. Regressionsalgoritmen kan betragte et lokalt minimum som korrekt. Så for at bestemme det korrekte globale minimum er det klogt at sammenligne resultaterne med øjnene for den laveste MSE.

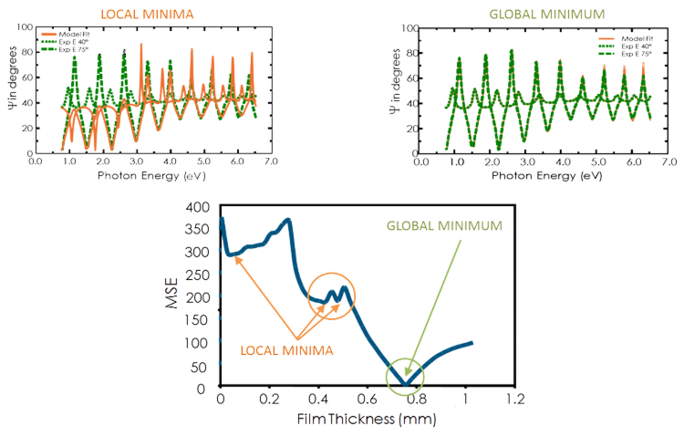
Figur 11, øverst til højre: Eksperimentelle data og tilsvarende kurver genereret for modellen ved det globale minimum. Figur 11, øverst til venstre: En lignende kurve ved det lokale minimum nær en tykkelse på 0,45 µm kan let identificeres som et ukorrekt resultat. Figur 11, nederst: MSE-kurven i forhold til tykkelsen viser det globale minimum. En regressionsalgoritme kan give lokale minima, men ikke det endelige resultat.

Bestemmelse af filmtykkelse

Filmtykkelse bestemmes normalt ved interferens mellem det lys, der reflekteres fra overfladen, og det lys, der bevæger sig gennem filmen. Om denne interferens betragtes som konstruktiv eller destruktiv afhænger af den relative fase af det lys, der slutter sig til overfladerefleksionen. Interferencen indeholder både amplitude- og faseinformation. Faseinformationen fra Δ er meget følsom over for film ned til sub-monolagstykkelse. Se nedenstående figur for en sammenligning af den reflekterede intensitet og ellipsometri for den samme serie af tynde SiO2-lag på Si. Reflektansen for hver film er næsten den samme, mens der er store variationer i Δ.

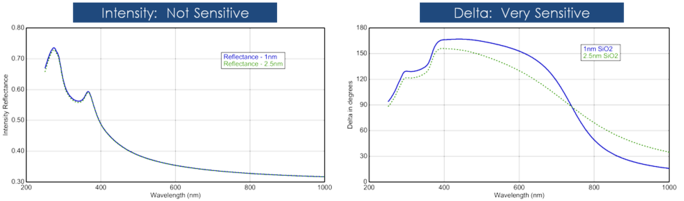
Figur 12, venstre: Reflekteret intensitet og ellipsometrisk delta (højre) for to tynde oxider på silicium. Intensitetsmålingen viser ikke, at Delta er meget følsom over for film i nanometerstørrelse.

Ellipsometri anvendes almindeligvis til film fra sub-nanometer til et par mikrometer tykkelse. Ved film, der er tykkere end flere tiendedele mikrometer, kan interferencesvingninger kun opløses med stigende vanskeligheder, undtagen når der anvendes længere infrarøde bølgelængder. Derfor anvendes der til tykkere film normalt andre måleteknikker.

For at måle tykkelsen skal en del af lyset passere gennem hele filmen og derefter vende tilbage til overfladen. Med lysabsorberende materialer kan optiske tykkelsesmålinger kun udføres på tynde og halvt uigennemsigtige lag, medmindre de udføres på spektralområder med mindre absorption. F.eks. kan en organisk film, der absorberer UV- og IR-lys, være gennemsigtig ved midtsynlige bølgelængder. Metaller absorberer kraftigt ved alle bølgelængder, så den maksimale lagtykkelse, der kan bestemmes, ligger omkring 100 nm.

Optiske konstanter

Optiske konstanter spiller en vigtig rolle for tykkelsesmålinger. En films tykkelse har indflydelse på lysets vejlængde, der bevæger sig gennem filmen, og indekset bestemmer lysbølgens hastighed og brydningsvinkel. Begge dele bidrager derfor til forsinkelsen mellem lys, der bevæger sig gennem filmen, og overfladerefleksionen. Det er nødvendigt at fastslå n og k samt tykkelsen for at opnå korrekte resultater af en optisk måling.

Da et materiales optiske konstanter varierer for forskellige bølgelængder, skal alle bølgelængder, der analyseres med ellipsometeret, bestemmes individuelt. Et materiales respons ved hver bølgelængde kan forudses ved hjælp af en tabel over optiske konstanter. For at undgå den besværlige justering af ukendte optiske konstanter bølgelængde for bølgelængde er det fordelagtigt at anvende alle bølgelængder samtidig. De justerbare parametre i en dispersionsrelation gør det f.eks. muligt at tilpasse den samlede optiske konstantform til de eksperimentelle resultater. I forhold til at justere individuelle n og k-værdier for hver bølgelængde reduceres antallet af ukendte frie parametre betydeligt.

Cauchy- eller Sellmeier-relationer anvendes ofte til at beskrive indekset for transparente materialer, hvor Cauchy-relationen normalt angives som:

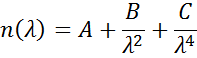
med de tre termer tilpasset for at matche brydningsindekset for materialet. Cauchy-forholdet er ikke begrænset af Kramers-Kronigs (KK) konsistens og kan føre til ufysisk dispersion. Sellmeier-relationen på den anden side pålægger Kramers-Kronig-konsistens (KK), som sikrer, at den optiske dispersion bevarer en realistisk form. Sellmeier-relationen skrives typisk som:

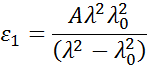
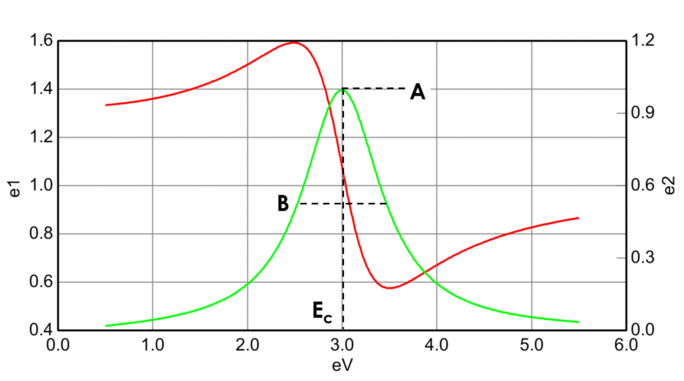
Absorberende materialer har ofte et transparent bølgelængdeområde, der kan modelleres med Cauchy- eller Sellmeier-relationen. Mens det absorberende område imidlertid skal tage højde for både reelle og imaginære optiske konstanter. For at beskrive absorptionen for forskellige materialer anvender mange dispersionsrelationer oscillatorteori, herunder Lorentz-, Harmonic- og Gauss-teori, til at beskrive absorptionen for forskellige materialer. Alle har de samme egenskaber, idet absorptionsegenskaberne beskrives ved hjælp af Amplitude, Udvidelse og Centerenergi (relateret til lysets frekvens). Formen af den reelle komponent beregnes ved hjælp af Kramers-Kronig-konsistensen, efter at den imaginære adfærd er beskrevet af oscillatoren. For at medtage eventuel ekstra absorption uden for det målte spektralområde tilføjes der en forskydning til den reelle komponent. Lorentzoscillatoren kan skrives som:

Figur 13 viser også Amplitude (A), Udvidelse (B), Centrenergi (Ec) og offset (e1, off set) for en typisk Lorentzoscillator. Energien E er relateret til en bølges frekvens, n:

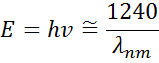
Planck-konstanten h og bølgelængden λ er angivet i nanometer. Andre dispersionsmodeller, som Tauc-Lorentz og Cody-Lorentz, indeholder udtryk til beskrivelse af bandgap-energien.

Videre læsning

Ellipsometri er en etableret optisk teknik til måling af tynde film og bulkmaterialer. Den bruger de polarisationsændringer, der forårsages af refleksion/transmission fra en materialestruktur, til at bestemme materialets egenskaber som tykkelse og optiske konstanter.

Aspnes D.E. (1985). Nøjagtig bestemmelse af optiske egenskaber ved hjælp af ellipsometri. In: Palik E.D. (ed.) Handbook of Optical Constants of Solids, pp. 89-112. Academic Press, Orlando.

Azzam R.M.A. og Bashara N.M. (1987). Ellipsometry and Polarized Light, Elsevier Science B.V., Amsterdam, Nederlandene.

Boccara A.C., Pickering C. og Rivory J. (eds.), (1993). Spectroscopic Ellipsometry, Elsevier Publishing, Amsterdam.

Collins R.W., Aspnes D.E., and Irene E.A. (eds.), (1998). “Proceedings from the Second International Conference on Spectroscopic ellipsometry”. In: Thin Solid Films, vols. 313-314.

Fujiwara H., Spectroscopic Ellipsometry, Principles and Applications, John Wiley & Sons, Ltd. 2007

Gottesfeld S., Kim Y.T., og Redondo A. (1995). “Recent applications of ellipsometry and spectroellipsometry in electrochemical systems”, In: I. Rubinstein (red.), Physical Electrochemistry: Principles, Methods, and Applications, Marcel Dekker, New York.

Herman, I.P. (1996). Optical Diagnostics for Thin Film Processing, pp 425-479. Academic Press, San Diego, Californien.

Johs B. et al (1999). “Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part II: Advanced Applications”. Optical Metrology, vol. CR72, pp 29-58. SPIE, Bellingham, Washington.

Johs B. et al (2001). “Recent Developments in Spectroscopic Ellipsometry for in situ Applications”. In: Duparré A, Singh B (red.) Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II, vol. 4449, pp 41-57. SPIE, Bellingham, Washington.

Roseler A. (1990). Infrared Spectroscopic Ellipsometry, Akademie-Verlag, Berlin.

Rossow U. og Richter W. (1996). “Spektroskopisk ellipsometri” i: “Spectroscopic Ellipsometry” i: Bauer G and Richter W (eds.) Optical Characterization of Epitaxial Semiconductor Layers, pp. 68-128, Springer-Verlag, Berlin.

Tompkins H.G. (1993). A User’s Guide to Ellipsometry, Academic Press, San Diego, Californien.

Tompkins H.G. og McGahan W.A. (1999). Spectroscopic Ellipsometry and Reflectometry, John Wiley & Sons, Inc, USA.

Tompkins, H.G. og Irene E.A. (eds.), 2005, Handbook of Ellipsometry, William Andrew Publishing, New York.

Tompkins, H. G. og Hilfiker, J. H., Spectroscopic Ellipsometry, Practical Application to Thin Film Characterization, 2016, Momentum Press Engineering

Woollam J.A. og Snyder P.G. (1992). “Variable Angle Spectroscopic Ellipsometry” i: “Variable Angle Spectroscopic Ellipsometry” i: Brundle CR, Evans CA, og Wilson S (eds) Encyclopedia of Materials Characterization: Surfaces, Interfaces, Thin Films, pp. 401-411, Butterworth-Heinemann, Boston.

Woollam J.A. et al (1999). “Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part I: Basic Theory and Typical Applications” (Oversigt over spektroskopisk ellipsometri med variabel vinkel (VASE), del I: Grundlæggende teori og typiske anvendelser). Optical Metrology, vol. CR72, pp 3-28. SPIE, Bellingham, Washington.

Woollam J.A. (2000). “Ellipsometry, Variable Angle Spectroscopic” i: Webster J.G. (red.) Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 109-116. John Wiley & Sons, New York.