Ising-modellen er et særligt eksempel på et termodynamisk system, og det er et modelsystem til at forstå faseovergange. Ved du, hvordan så mange biologer bruger så meget tid på sølle frugtfluer? Jamen, fysikere bruger meget tid på Ising-modellen. Som professor Raghu hjælpsomt fortæller os, er det faseovergangernes Drosophila.

Personligt er jeg ikke den største tilhænger af hans analogi, fordi jeg synes, at frugtfluer er ulækre. Forhåbentlig er Ising-modellen ikke for ulækker.

Motivation

Hvorfor skal vi bruge så meget tid på at tale om Ising-modellen?

• Den er overraskende nyttig til at hjælpe os med at tænke over alle mulige former for adfærd i forbindelse med faseovergange. For eksempel:

  • Ising-modellen udviser symmetribrud i lavtemperaturfasen (som vi lige har talt om)

  • den har et særligt “kritisk punkt” ved en veldefineret temperatur (som vi hentydede til i vandets fasediagram)

  • andre rige egenskaber.

• Det er en af de få nøjagtigt opløselige modeller, hvor vi faktisk kan beregne termodynamiske størrelser og fortolke dem.

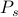  • Generelt er det svært at beregne termodynamiske størrelser, fordi man skal summere mange termer op. Husk fra vores første termokursus, at man kan tænke på et ligevægtssystem som et ensemble af mange tilstande , der hver især er vægtet med deres egen sandsynlighed . I denne ramme svarer de termodynamiske størrelser, som du observerer, til gennemsnit over ensemblet. Hvis man især ønsker at finde ensemblegennemsnittet af en eller anden observerbar størrelse 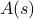, skal man finde summen 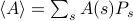, hvor summen løber over alle de mulige tilstande. Problemet med dette er, som du husker, at antallet af tilstande i et termodynamisk system skalerer eksponentielt med antallet af partikler! Selv for et system af moderat størrelse er der simpelthen for mange tilstande til, at en computer eksplicit kan beregne gennemsnittet – for slet ikke at tale om et termodynamisk system, hvor 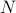er i størrelsesordenen .

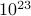  • Så vi skal ”være kloge” for at beregne fordelingsfunktionen, og vi burde være taknemmelige for præcist opløselige systemer!

• Ising-modellen er enkel, men den kan alligevel anvendes på et overraskende antal forskellige systemer.

  • Dette er vores første smagsprøve på universalitet – et træk ved kritiske fænomener, hvor den samme teori gælder for alle mulige forskellige faseovergange, hvad enten det er i væsker og gasser eller magneter eller superledere eller hvad som helst. Fysikere elsker denne form for generel adfærd, fordi den antyder en slags dybere orden i vores kaotiske verden.

Definition af Ising-modellen

Ising-modellen er en matematisk model, der ikke svarer til et faktisk fysisk system. Det er et enormt (kvadratisk) gitter af steder, hvor hvert sted kan være i en af to tilstande. Vi mærker hvert site med et indeks , og vi kalder de to tilstande og . For at sige, at det ‘te site er i tilstanden , skriver vi .

Nu er denne definition sørgeligt abstrakt og ufysisk, så for os fysikere er det yderst nyttigt at have et konkret system i tankerne, så vi kan henvise til noget eksplicit og opbygge en fysisk intuition. Her er et par fysiske systemer, som Ising-modellen kan repræsentere:

• En magnet. Hvert sted repræsenterer et bestemt “spin” i materialet (en uparret elektron??), og det er , hvis spinnet peger nedad, eller , hvis spinnet peger opad. Hvert af spinnene opfører sig som en mini-magnet med sit eget mini-magnetiske moment; hvis alle spinnene er justeret, opfører hele gitteret af spinnene sig som en stor magnet med et makroskopisk magnetisk nettomoment.

• En legering; lad os sige messing. Hvert af stederne er et atom i gitteret; repræsenterer et kobberatom på det pågældende sted; repræsenterer zink.

• En ”gittergas”. Hvert af stederne er den mulige placering af en partikel; betyder, at stedet er tomt, og betyder, at stedet er besat af en partikel.

• Bakterielle vortexgitter???

For nu vil vi tænke på Ising-modellen som en model for en magnet. Det er ganske vist en groft forenklet og legetøjsmodel af en magnet, men magnetanalogien kan ikke desto mindre være med til at vejlede vores forkætrede fysiske intuition.

Sammensætning af Hamiltonianen

Et naturligt spørgsmål at stille om denne Mickey-mouse-model af en magnet er, hvilken energi den har. For at være mere præcis ønsker vi at nedskrive en funktion, der repræsenterer energien for hver enkelt mulig konfiguration (også kaldet mikrotilstand) af spinnene i magneten. Som bekendt kaldes denne energifunktion for Hamiltonianen.

I Ising-modellen omfatter Hamiltonianen to typer af vekselvirkninger:

• det eksterne feltterm. Som vi husker fra kvantemekanikken, kan et eksternt magnetfelt dele energierne i spin-down- og spin-up-tilstanden, så den ene er højere i energi og den anden er lavere.

  • Størrelsen af repræsenterer, hvor stærkt feltet er, så det fortæller, hvor meget højere i energi det ene spin er end det andet.

  • Tegnet på fortæller, om det er spin-up eller spin-down, der er foretrukket.

  • Da hvert enkelt spin mærker det ydre felt, er vi nødt til at summere over alle steder for at finde det samlede bidrag til energien.

• interaktionstermen mellem nabospin – måske vil de flugte med hinanden og pege samme vej, måske vil de anti-flytte og pege på forskellige måder. Fysisk set kan vi forestille os, at denne vekselvirkning opstår, fordi hvert spin i magneten er sin egen mini-magnetiske dipol, der opretter sit eget magnetfelt, og dets naboer kan mærke dette magnetfelt.

  • Størrelsen af fortæller, hvor stærkt nabospinene er koblet til hinanden – hvor meget de ønsker at (anti-)rette sig ud. Fysisk set kunne styrken af spin-spin-koblingen f.eks. afhænge af afstanden mellem dem i magets gitter.

  • Tegnet på fortæller dig, om naboerne foretrækker at flugte eller at anti-flytte. (Den tekniske betegnelse for dette er henholdsvis ferromagnetisk eller anti-ferromagnetisk). Fysisk set afhænger det af de nøjagtige kvantemekaniske detaljer om, hvordan spins interagerer, om et materiale er det ene eller det andet (eller ingen af delene).

  • Da spin-spin-interaktionen opstår mellem to spins, er vi nødt til at summere over par af steder for at finde dens samlede interaktion til energien.

Mere om vekselvirkningstermen

Et naturligt spørgsmål om spin-spin vekselvirkningstermen er, hvilke spins er koblet til hvilke spins?

Hvis vi igen vender tilbage til det fysiske billede af magneten, og vi zoomer ind på et bestemt spin, vil vi forvente, at styrken af spin-spin vekselvirkningen er stærkere for nærliggende spins og svagere for fjerntliggende spins. Den nøjagtige afstandsafhængighed af spin-spin-interaktioner er sandsynligvis ret kompliceret for faktiske magneter.

For Ising-modellen gør vi den enkleste mulige antagelse for karakteren af denne spin-spin-interaktion:

Et par kommentarer:

• I et kvadratisk gitter med dimensioner har hvert sted 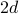nærmeste naboer: venstre og højre i én dimension, op og ned, når man tilføjer den anden dimension, osv…

• Vi antager, at interaktionen er isotropisk – alle naboer behandles ens uanset retning.

• Vi taler ofte om nærmest-nabo-interaktioner som energien af en binding, der forbinder to gitterpladser.

• Når vi summerer over tilstødende par af steder, skriver vi symbolsk set små vinkelparenteser omkring indeksene for at repræsentere ”nærmeste nabo”.

En fin konsekvens af nærmeste nabo-interaktioner er, at når vi finder den samlede energi for en eller anden konfiguration af spins, så summerer vi i stedet for at summere over alle mulige par af steder, kun over par af steder, der er tilstødende til hinanden.

Nu, hvor vi har diskuteret alle disse ting, er vi klar til at skrive det egentlige udtryk for Hamiltonianen ned. (Jeg ville gerne forklare og fortolke fysikken, før jeg skrev Hamiltonianen ned, så symbolerne gav nogenlunde mening.)

Hamiltonianen for Ising-modellen

Hamiltonianen for Ising-modellen kan skrives som

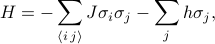
hvor repræsenterer spin-spin vekselvirkningen, repræsenterer det eksterne felt, og sigma_j er de individuelle spins på hver af gitterpladserne. Den første sum er over alle par af nabogitterpladser (også kaldet bindinger); den repræsenterer vekselvirkningerne mellem spins. Den anden sum er over alle gitterpladserne selv; den repræsenterer det eksterne felt, der forsøger at justere alle spins i én retning.

Fortsæt til termodynamikken i Ising-modellen.