af Marco Taboga, PhD
Indikatorfunktionen for en begivenhed er en tilfældig variabel, der har værdien 1, når begivenheden finder sted, og værdien 0, når begivenheden ikke finder sted. Indikatorfunktioner anvendes ofte i sandsynlighedsteori for at forenkle notation og for at bevise sætninger.
Definition
Det følgende er en formel definition.
Definition Lad 
være et prøverum og være en begivenhed. Indikatorfunktionen (eller den tilfældige indikatorvariabel) for hændelsen , betegnet , er en tilfældig variabel, der er defineret som følger: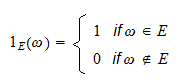
Mens indikatoren for en begivenhed normalt betegnes med , betegnes den undertiden også medhvor er det græske bogstav Chi.
Eksempel Vi kaster en terning, og et af de seks tal fra 1 til 6 kan fremkomme med forsiden opad. Prøverummet erDefinér hændelsen beskrevet ved sætningen “Et lige tal vises med forsiden opad”. En tilfældig variabel, der får værdien 1, når et lige tal vises med forsiden opad, og værdien 0 i modsat fald, er en indikator for hændelsen . Den konkrete definition af denne indikator er
Ud fra ovenstående definition kan det let ses, at er en diskret tilfældig variabel med støtte og sandsynlighedsmassefunktion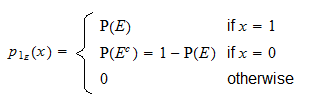
Egenskaber
Indikatorfunktioner nyder godt af følgende egenskaber.
Powerer
Den -te potens af er lig med :fordi kan være enten eller og
Forventet værdi
Den forventede værdi af er lig med :
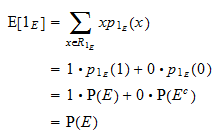
Varians
Variansen af er lig med . Takket være den sædvanlige variansformel og ovenstående potensegenskab får vi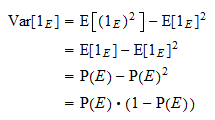
Intersektioner
Hvis og er to hændelser, så erfordi:
-
hvis
, så og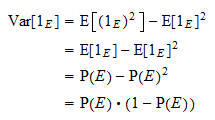
-
hvis
, såog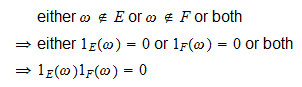
Indikatorer for nul-sandsynlighedsbegivenheder
Lad være en nul-sandsynlighedsbegivenhed og en integrerbar tilfældig variabel. Så,Selv om et stringent bevis for denne kendsgerning ligger uden for rammerne af denne indledende redegørelse, bør denne egenskab være intuitiv. Den tilfældige variabel er lig med nul for alle prøvepunkter undtagen muligvis for punkterne . Den forventede værdi er et vægtet gennemsnit af de værdier kan antage, hvor hver værdi er vægtet med sin respektive sandsynlighed. De værdier, der ikke er nul, som kan antage, er vægtet med sandsynlighederne nul, så må være nul.
Løste opgaver
Nedenfor finder du nogle opgaver med forklarede løsninger.
Ovelse 1
Betragt en tilfældig variabel og en anden tilfældig variabel , der er defineret som en funktion af .
Udtryk ved hjælp af indikatorfunktionerne for hændelserne og .
Angiv med indikatoren for hændelsen og anfør med indikatoren for hændelsen . Vi kan skrive som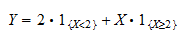
Ovelse 2
Lad være en positiv tilfældig variabel, det vil sige en tilfældig variabel, der kun kan antage positive værdier. Lad være en konstant. Bevis, at hvor er indikatoren for hændelsen .
Først skal man bemærke, at summen af indikatorerne og altid er lig med :Som følge heraf kan man skrive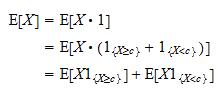
Nu skal man bemærke, at er en positiv tilfældig variabel, og at den forventede værdi af en positiv tilfældig variabel er positiv:Dermed,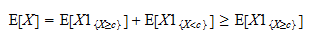
Ovelse 3
Lad være en begivenhed og betegne dens indikatorfunktion med . Lad være komplementet til og betegne dets indikatorfunktion med . Kan du udtrykke som en funktion af ?
Summen af de to indikatorer er altid lig med :Derfor,
Hvordan citeres
Please cite as:
Taboga, Marco (2017). “Indikatorfunktioner”, Forelæsninger om sandsynlighedsteori og matematisk statistik, tredje udgave. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-probability/indicator-functions.