- Hvad er hældningsinterceptformen
- Hvad er b i y=mx+b?
- Hvad er m i form af hældningsskæring?
- Hvordan skriver man en ligning i hældningsintervalform?
- Hvordan finder man y-interceptet?
- Hvordan finder man hældningen af en ligning?
- Hvad er en udefineret hældning?
- Finding af ligning ud fra et punkt
- Find hældning ud fra to punkter
- Ligning for en linje givet to punkter
- Hvordan finder man domæne og rækkevidde?
Hvad er hældningsinterceptformen
Hældningsinterceptformen er en af de tre former, vi kan bruge til at udtrykke en ret linje. De andre former kaldes punkthældningsform og standardform, men vi vil for det meste bruge hældningsinterceptform i dette afsnit. Ved at bruge hældningsskæringform udtrykker vi ligningen for en linje således:
Du kender måske xxx og yyy til at være koordinater for et punkt på en graf, men hvad er mmm og bbb?
Hvad er b i y=mx+b?
Bogstavet b er et tal, der repræsenterer, hvornår linjen rører y-aksen. Vi omtaler også dette som “y-interceptet”. Lad os f.eks. tegne en ret linje på koordinatplanet.
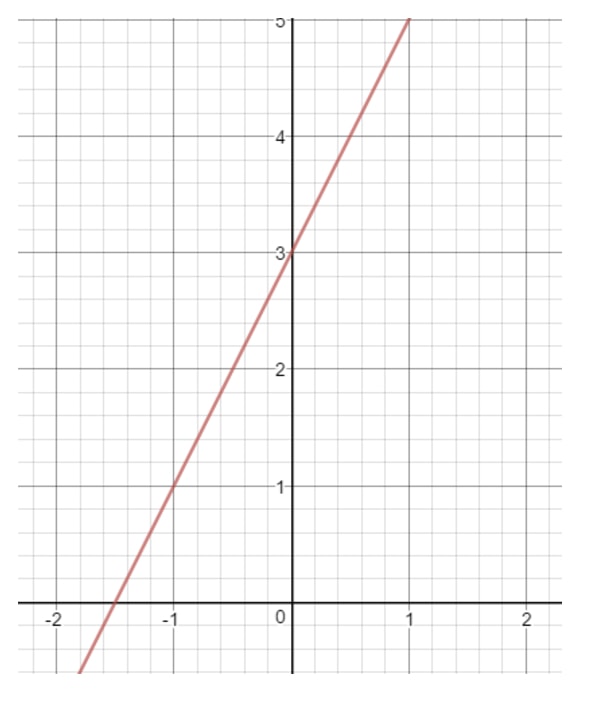
Hvis du kigger nærmere på y-aksen, rører den rette linje y-aksen et bestemt sted. Hvor er dette sted? Det ville være tallet 3, fordi det er der, hvor y-aksen og den rette linje skærer hinanden. Det betyder, at vi kan konkludere, at b = 3.
Hvad er m i form af hældningsskæring?
Bogstavet m er et tal, der repræsenterer linjens hældning. Nogle mennesker omtaler hældningen som stigning over løb. Husk, at hvis vi har to punkter, kan vi finde hældningen af de to punkter ved at bruge hældningsformlen
Den samme idé virker her. Hvis vi tager to vilkårlige punkter på en ret linje, så kan vi finde hældningen af linjen ved hjælp af ovenstående formel! Lad os f.eks. bruge denne linje.
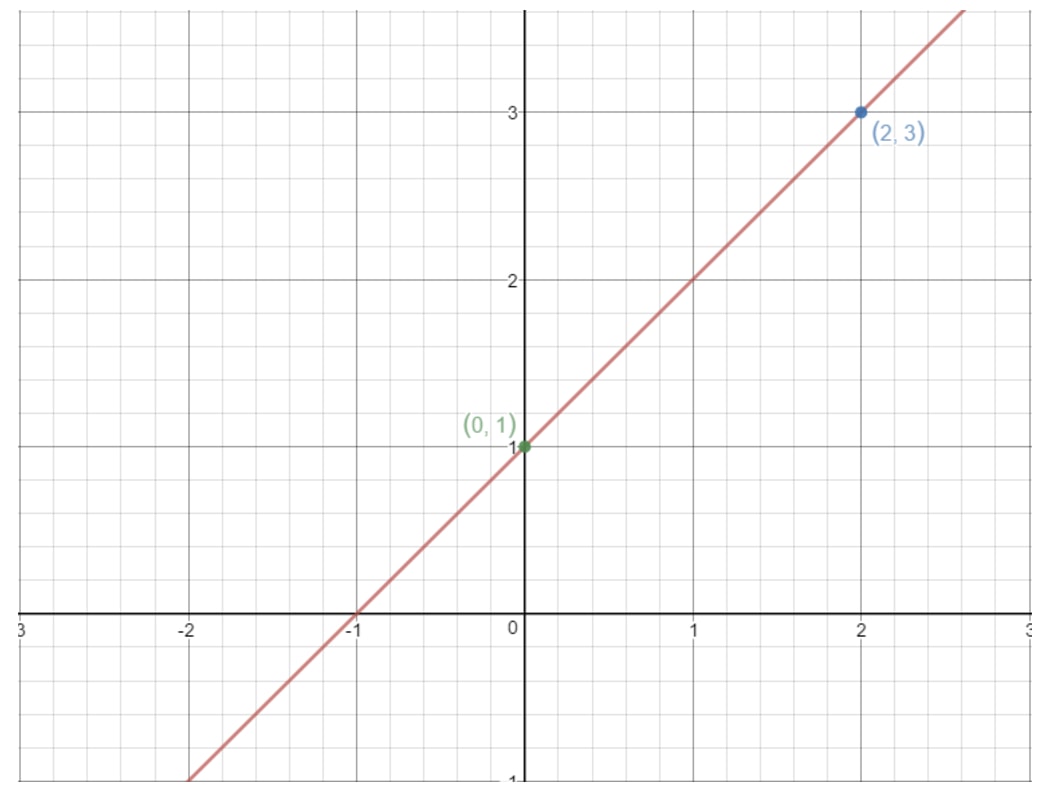
Bemærk, at punkterne (2, 3) og (0, 1) ligger på denne graf. Så hvorfor bruger vi ikke disse to punkter til at finde hældningen på linjen? Ved at bruge formlen ville vi få:
Det betyder, at hældningen af denne linje er 111!
Det særlige ved hældninger er, at vi kan bruge to vilkårlige punkter på linjen til at finde den. Så hvis du tog to forskellige punkter på denne linje, ville du stadig få, at hældningen er 111.
Hvordan skriver man en ligning i hældningsintervalform?
Du ved måske, hvordan hældningsintervalformen ser ud, men halvdelen af tiden får du ligninger, der ikke er i denne form. Så det er din opgave at omdanne den til hældningsinterceptform. Hvordan gør vi det? Målet er altid at isolere yyy-terminen. Lad os f.eks. sige, at du får ligningen
For at isolere yyy, flytter vi 6x+46x + 46x+4 til højre side af ligningen
Nu er 222 i vejen for yyy, så vi skal af med den ved at dividere begge sider af ligningen med 222.
Da yyy er isoleret, kan man se, at det er i hældningsinterceptformen y=mx+by = mx + by=mx+b hvor m=-3m = -3m=-3, og b=-2b = -2b=-2.
Nu da vi kender y-interceptet og hældningen rigtig godt, hvorfor ser vi så ikke på specifikke spørgsmål om at finde dem!
Hvordan finder man y-interceptet?
Spørgsmål 1: Ved hjælp af den lineære ligning y=12x+5y = \frac{1}{2} x + 5y=21x+5, find y-interceptet.
Bemærk her, at ligningen allerede er i hældningsinterceptformen y=mx+by = mx + by=mx+b. Vi skal bare finde ud af, hvad bbb er. Vi kan se, at b=5b = 5b=5, så y-interceptet er 555.
Lad os lave et lidt sværere spørgsmål.
Spørgsmål 2: Bestem y-interceptet for 2x-4y=82x – 4y = 82x-4y=8
Nu er denne lineære ligning ikke i hældningsinterceptform, så vi er nødt til at ændre den til denne form først. Vores mål er at isolere yyy i denne ligning.
Se, at hvis vi flytter 2x2x2x til højre side af ligningen, får vi:
Nu dividerer vi begge sider med -4-4-4, så får vi:
Nu får vi ved at dividere begge sider med -4-4-4:
Nu får vi ved at bytte om på de to termers positioner:
Spørgsmål 3: Bestem y-skæringspunktet for 4y-8=04y – 8 = 04y-8=0.
Dette ser måske lidt mærkeligt ud, fordi der ikke er noget xxx-terminus, men vores mål er stadig det samme. Vi skal isolere yyy.
Om vi flytter -8-8-8-8 til højre side af ligningen, får vi:
Dividerer vi begge sider af ligningen med 444, får vi
Nu ser det måske ikke sådan ud, men ligningen er i hældningsinterceptform. Det er bare sådan, at m=0m = 0m=0, så hele mxmxmxmx-terminen er forsvundet. Du skal bare omskrive ligningen som
Da du observerer, kan du se, at b=2b = 2b=2, og derfor er y-interceptet 222. Lad os lave et spørgsmål mere.
Spørgsmål 4: Bestem (om muligt) y-skæringspunktet for 5x-15=05x – 15 = 05x-15=0.
Dette spørgsmål er interessant, fordi ligningen ikke har noget yyy-terminus. Så hvordan skal vi sætte den i form af hældningsintercept? Tja, det eneste, vi kan gøre lige nu, er at isolere for xxx, så lad os prøve det for nu.
Forsætter vi 151515 til højre side af ligningen, får vi:
Dividerer vi begge sider af ligningen, får vi:
Det giver:
Nu skal vi tegne dette på en graf. Bemærk, at i denne ligning er xxx tvunget til at være 333 og kan ikke være noget andet. Derimod står der ikke noget om yyy, så yyy kan være hvad som helst. Hvis vi skulle skrive en værditabel, får vi:
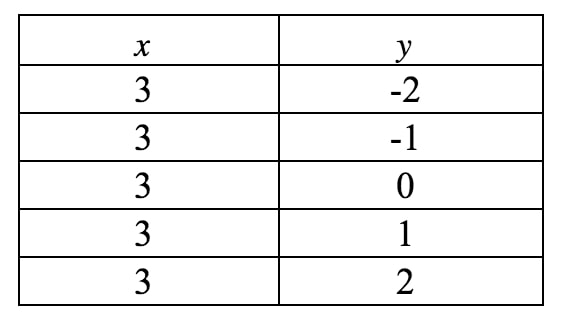
Hvis vi plotter disse punkter på et koordinatplan og tegner linjen, får vi:
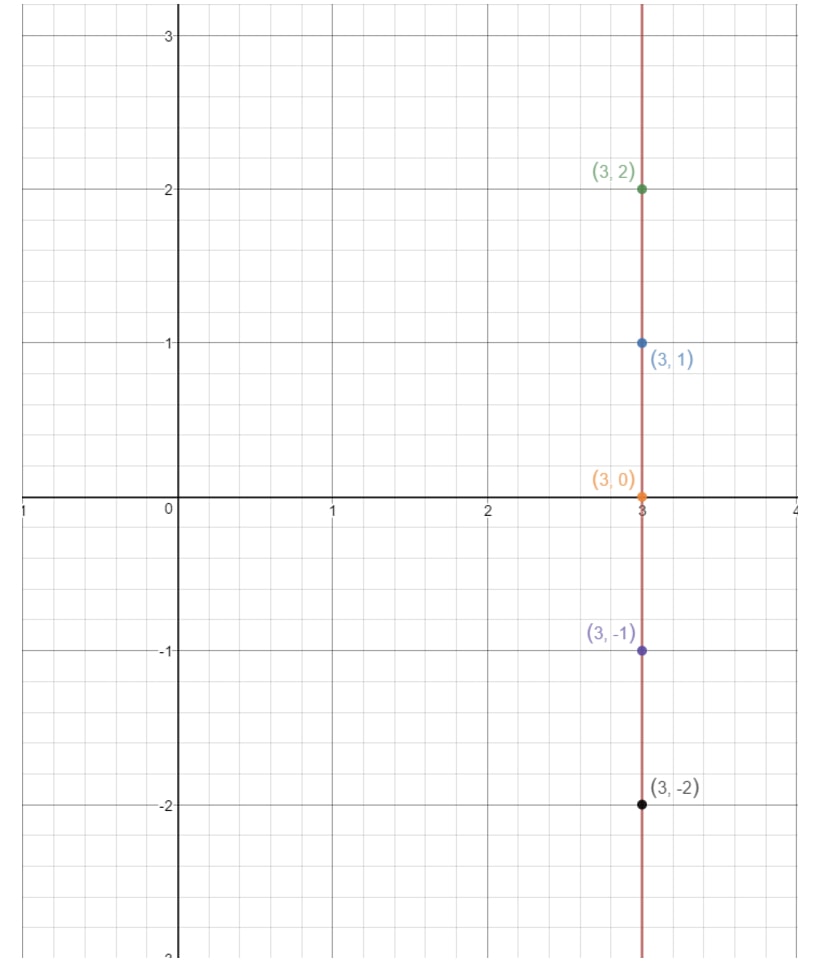
Bemærk, at linjen aldrig berører y-aksen. Det betyder, at ligningen ikke har et y-intercept. Nu hvor vi har dækket alle tilfælde af at finde y-skæringspunktet, lad os se på spørgsmål, der beder os om at finde hældningen!
Hvordan finder man hældningen af en ligning?
Spørgsmål 5: Find hældningen af y=32x+1y = \frac{3}{2}x + 1y=23x+1
Spørgsmål 6: Bestem hældningen af den lineære ligning 6x-6y=06x – 6y = 06x-6y=0
Som du kan se, er ligningen ikke i hældningsintervalform, så vi er nødt til at omdanne den til denne form først. Vores mål er at isolere yyy.
Forsætter vi 6x6x6x til højre side af ligningen, får vi:
Dividerer vi begge sider med -6-6-6-6, får vi:
Bemærk, at dette faktisk er i hældningsinterceptform y=mx+by = mx + by=mx+b. Det er bare det, at y-interceptet bbb i dette tilfælde er 000, og xxx er det samme som 1x1x1x. Så vi kan omskrive ligningen til:
Nu kan vi ved at observere se, at m=1m = 1m=1. Da mmm er hældningen, så må hældningen være 111. Lad os lave en lidt sværere
Spørgsmål 7: Bestem hældningen af 2y-4=02y – 4 = 02y-4=0
Og igen er dette lidt mærkeligt, fordi vi ikke har noget xxx-terminus. Vores mål om at isolere yyy forbliver dog det samme.
Ved at flytte -4-4-4-4 til højre side af ligningen får vi:
Dividerer vi begge sider af ligningen med 222, får vi:
Se her, at den nu er i hældningsinterceptform, bortset fra at udtrykket mxmxmx er skjult, fordi m=0m = 0m=0. Så vi kan omskrive vores ligning som:
Da m=0m = 0m=0, så har vi en hældning på nul. Hvis du undrer dig over, hvordan en linje med 000 hældning ser ud, så er her en graf, som du kan se:
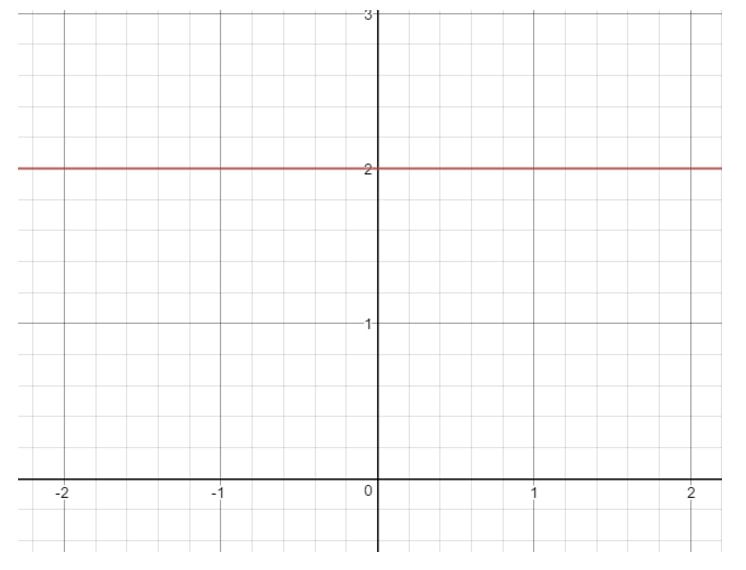
Spørgsmål 8: Find (om muligt) hældningen til den lineære ligning 16-4x=016 – 4x = 016-4x=0
I dette tilfælde kan yyy ikke isoleres, fordi der ikke er noget yyy-termin. Så det eneste, vi kan gøre, er at isolere xxx.
Forsætter man 161616 til højre side af ligningen, får man:
Dividerer man begge sider med -4-4-4-4, får man:
Dette er stadig ikke i hældningsintervalform, så vores eneste håb om at få fat i hældningen er at tegne en graf af denne linje. Igen ser vi, at xxx altid er tvunget til at være 444, men yyy kan være hvad den vil, fordi der ikke er nogen yyy-termin. Hvis vi skulle skrive en værditabel, får vi:
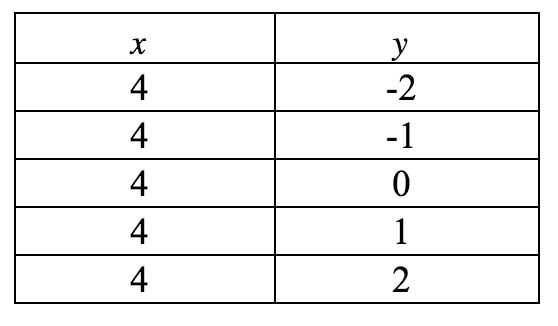
Hvis vi plotter disse punkter på et koordinatplan og tegner linjen, får vi:
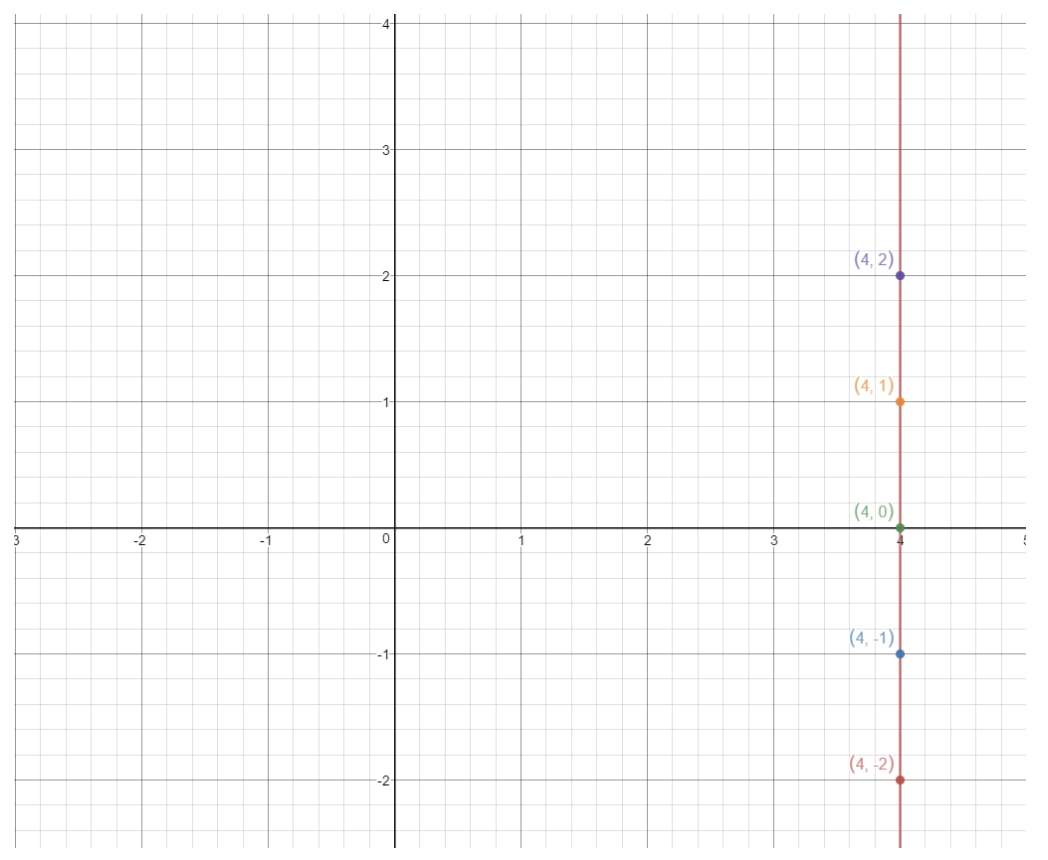
Dette er en lodret linje. Hvad er så hældningen på en lodret linje? Lad os prøve at finde ud af det ved at finde stigningen og løberne. Se, hvordan denne linje altid stiger uendeligt meget, men der er ingen løb overhovedet. Så det betyder, at løb er 000. Så hvis vi beregner hældningen, så får vi:
Vi kan ikke dividere med 000, så vi har faktisk en udefineret hældning.
Hvad er en udefineret hældning?
En udefineret hældning er en hældning, der går lige opad i grafen. Som det ses i grafen ovenfor, stiger hældningen i det uendelige og har ingen løb. Derfor får vi en udefineret hældning, fordi vi ikke kan dividere med 000.
Generelt får vi altid en udefineret hældning, når vi får en lige lodret linje!
Lad os se på nogle andre unikke spørgsmål!
Finding af ligning ud fra et punkt
Spørgsmål 9: Et punkt (2, 6) går gennem en ligning med y=-5x+by = -5x + by=-5x+b. Find “bbb”.
Isolering og løsning af bbb giver:
Husk, at bbb også er kendt som y-skæringspunktet, så y-skæringspunktet er også 16161616!
Find hældning ud fra to punkter
Spørgsmål 10: Givet to punkter (6, 1) og (-10, 9), find linjens hældning.
Husk, at for at finde linjens hældning bruger vi hældningsligningen
Dermed giver anvendelsen af denne formel os:
Hvad nu, hvis vi i stedet skal finde hele ligningen for en linje?
Ligning for en linje givet to punkter
Spørgsmål 11: Givet to punkter (-6, 1) og (2, 6), find ligningen i form af hældningsinterceptet.
Vi forsøger i princippet at finde ligningen i form af y=mx+by = mx + by=mx+b. For at gøre dette er vi nødt til at lede efter mmm og bbb.
Husk, at for at finde mmm bruger vi hældningsligningen
Dermed giver anvendelsen af denne formel os:
Så nu har vi ligningen
Nu skal vi lede efter bbb. For at løse bbb vælger vi et af de givne punkter og sætter det ind i ligningen. Det kan vi gøre, fordi begge punkter ligger på linjen, og ethvert punkt på linjen vil opfylde ligningen. Lad os bruge punktet (2, 6). Se at:
Isoleringen af bbb giver:
Sætter vi dette i decimalform, får vi, at b=4,75b = 4,75b=4,75. Derfor er vores ligning i form af hældningsintervallet ligning:
Den sidste ting, vi skal behandle i dette afsnit, er at finde en linjes domæne og rækkevidde.
Hvordan finder man domæne og rækkevidde?
For at finde en linjes domæne stiller vi i princippet os selv dette spørgsmål: Hvad kan xxx være? Hvis xxx kan være disse værdier, så tilføjer vi dem til domænet.
Det samme gælder for rækkevidde. Hvad kan yyy være? Hvis yyy kan være disse værdier, så tilføjer vi dem i intervallet. Lad os lave et eksempel.
Spørgsmål 12: Find domænet og intervallet for ligningen y=2x+1y = 2x + 1y=2x+1.
Bemærk, at hvis vi tegner grafen for denne linje, så får vi:
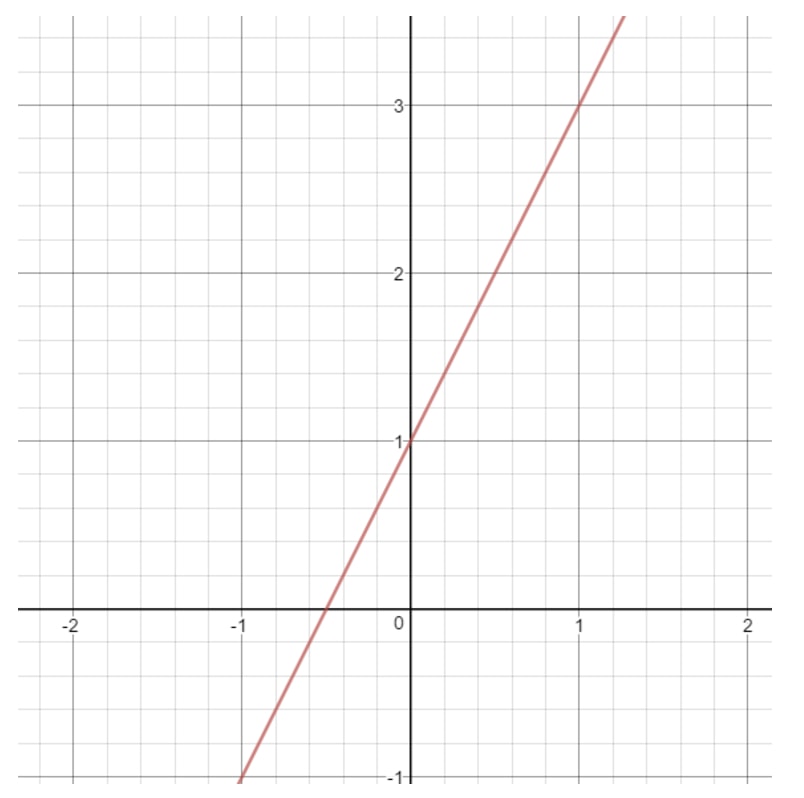
Hvad kan xxx være i denne linje? Bemærk, at xxx kan være hvad som helst, for med en hvilken som helst xxx-værdi kan vi få et punkt, der ligger på linjen. Det samme gælder for y. Vi kan altid vælge en yyy-værdi, der giver os et punkt på en linje. Så vi siger, at
hvor R betyder “alle reelle tal”. Lad os lave en sværere.
Spørgsmål 13: Find domænet og intervallet for ligningen y=-2y = -2y=-2.
Hvis vi nu tegner denne linje på en graf, får vi:
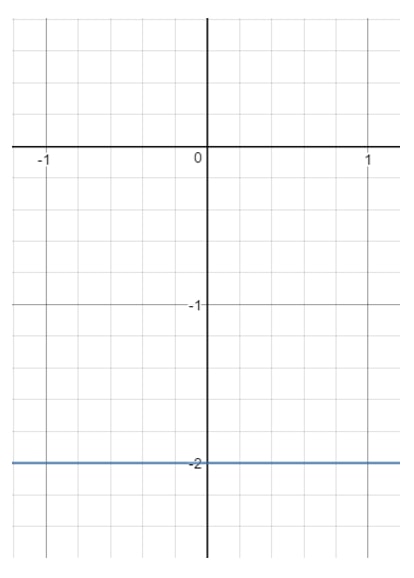
Bemærk, at xxx kan være hvad som helst, for med en hvilken som helst xxx-værdi kan vi få et punkt, der ligger på linjen, så længe y=-2y = -2y=-2. Se dog på yyy. Du ser, at yyy er tvunget til at være -2-2-2-2 og kan ikke være noget andet. I det øjeblik du vælger en anden yyy-værdi (f.eks. 111), så vil dette punkt ligge uden for linjen. Så det betyder:
Spørgsmål 14: Find domæne og rækkevidde for ligningen x=1x = 1x=1.
Hvis vi nu tegner denne linje på en graf, får vi:
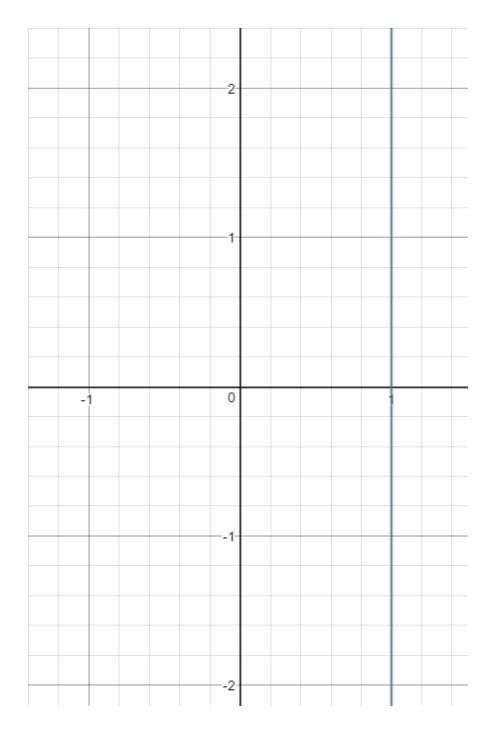
Du ser, at xxx er tvunget til at være 111 og kan ikke være noget andet. I det øjeblik du vælger en anden xxx-værdi (f.eks. 222), så vil dette punkt være ude af linjen. men se på yyy. Bemærk, at yyy kan være hvad som helst, for med en hvilken som helst yyy-værdi kan vi få et punkt, der ligger på linjen, så længe x=1x = 1x=1
Så det betyder:
Hvis du havde mange problemer med at tegne graferne for at få domæne og område, vil jeg anbefale dig at bruge denne lommeregner.
https://www.desmos.com/calculator/2rnqgoa6a4
Den lærer dig, hvordan man tegner en lineær ligning. Det eneste, du skal gøre, er at indtaste værdierne for mmm og bbb. Så vil den automatisk tegne linjen for dig! Det er også nyttigt, når du forsøger at finde hældningsintervalformen.