Hvordan laver vi en Guinier-tilpasning?¶

Guinier-approksimationen holder kun, når eksponentialet \(\exp(-q^2 R_g^2 /3)\)\)er lille. Det betyder, at vi for at opnå en god Guinier-tilpasning skalqRg være tilstrækkelig lille. Den qRg-værdi, ved hvilken Guinier-approksimationen begynder at svigte for en given spredningsprofil, afhænger af spredningselementets overordnede form. Nedenfor er vist en figur, der viser Guinier-approksimationen (sort) og spredningsintensiteten for en kugle, en tynd stang og en tynd skive (alle med samme Rg).

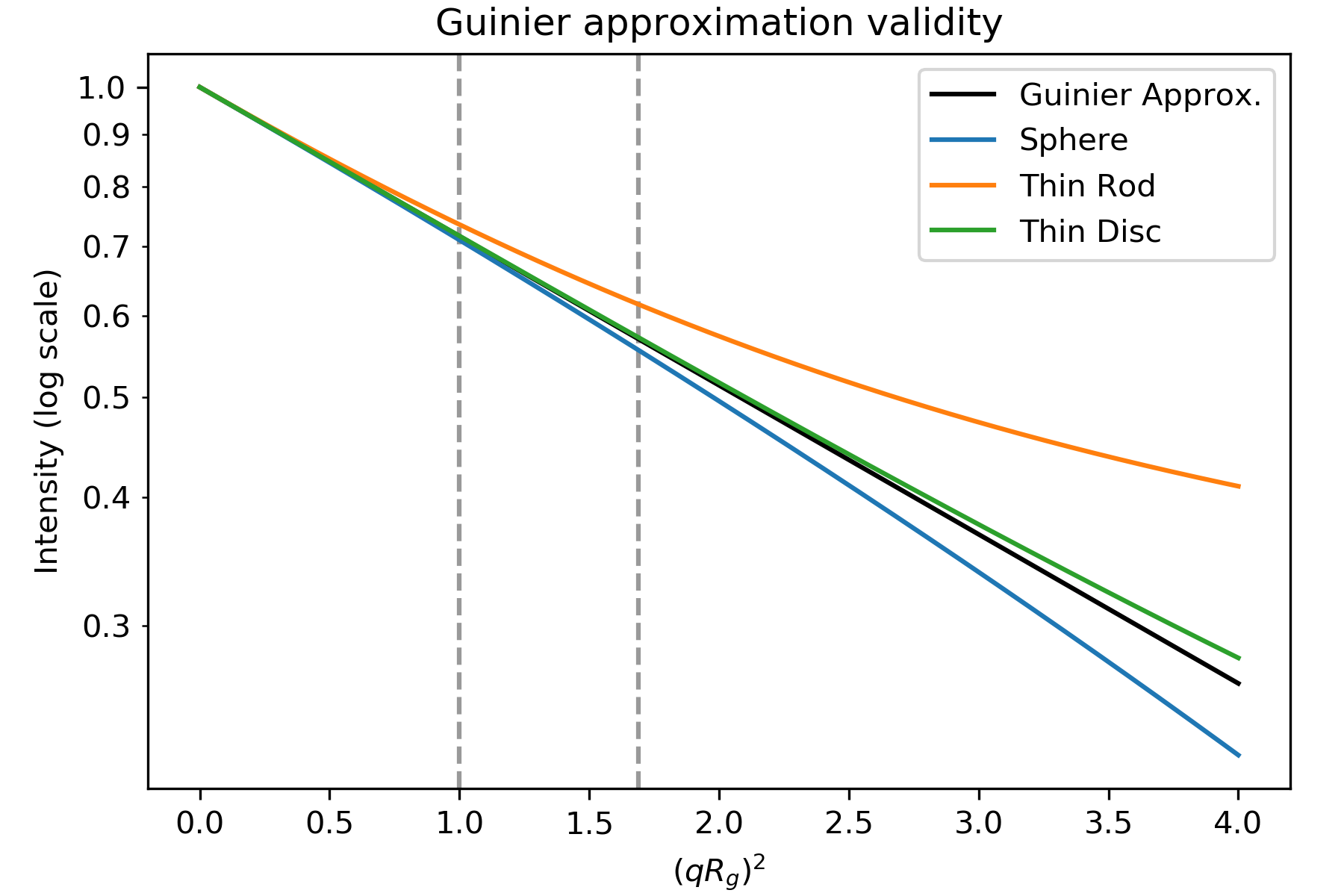
Plot baseret på figur 3.3 i . Intensitet for de geometriske former fra tabel 3.4 i . De stiplede linjer er ved qRg på 1,0 og 1,3((qRg) 2 på 1,0 og 1,69).

Som det fremgår, stemmer spredningsintensiteten for staven kun overens med Guinier-approksimationen indtil \(qR_g\sim 1,0\), kuglen indtil \(qR_g\sim 1,3\) og disken indtil \(qR_g\sim 1,7\). Afhængigt af den overordnede partikelform skal man således tilpasse forskellige mængder af data med lav q-værdi for at opnå en god Guinier-tilpasning. (Bemærk:Plottets x-akse er (qRg) 2, så \(qR_g\sim 1,3\) vises som den stiplede linje ved 1,69)

I praksis tilpasser vi både kugleformede (kugle- og skiveformede) objekter indtil \(qR_g\sim 1,3\).mens vi tilpasser stærkt udstrakte (stavformede) objekter indtil \(qR_g\sim 1,0\). Disse værdier blev valgt for at opnå <10% fejl som følge af afvigelsen af den faktiske form fra Guinier-approksimationen.Grunden til, at vi accepterer så stor en afvigelse, er, at man også får usikkerhed ved at tilpasse færre punkter i dataene, så der er en afvejning mellem, hvor godt approksimationen fungerer (tilpasning til mindre maksimal qRg) og hvor godt man kan tilpasse dataene (tilpasning til større maksimal qRg).

Guinier-tilpasningsområdet er således ideelt set fra den tidligst tilgængelige q-værdi til et maksimalt qRg på 1,0 eller 1,3. Men eftersom Rg er afledt af Guinier-fittet, hvordan bestemmer man så den korrekte maksimale q-værdi for slutningen af fitet? Svaret er, at Guinier-fitningen udføres iterativt:

1. Giv en maksimal q-startværdi for fitningen.
2. Beregn Guinier-fitningen og få Rg.
3. Hvis qmaxRg > 1,3 (eller 1,0), reduceres den maksimale q. HvisqmaxRg < 1,3 (eller 1,0), øges den maksimale q.
4. Gentag trin 2 og 3, indtil du konvergerer mod en endelig maksimal q-værdi.

De fleste programmer i dag vil udføre denne iterative søgning for dig, og for data af god kvalitet vil de give dig en rimelig maksimal q-værdi, som måske kun har brug for en smule manuel forfining.

Minimum q-værdien for en Guinier-tilpasning bestemmes normalt af den mindste tilgængeligeq -værdi i dine data, som er fastsat af det instrument, som du foretager målingen på.Det er dog vigtigt at have en tilstrækkelig lille minimum q for at have en rimelig rækkevidde for Guinier-tilpasningen. Typisk bør den mindste qRg-værdi være\(qR_g\leq 0,65\), selv om det for kuglesystemer kan være i orden at have\(qR_g\leq 1,0\). Det betyder, at den mindste q-værdi, der kræves, afhænger af størrelsen af det målte system. I nogle tilfælde, med særligt store systemer, kan det være nødvendigt bevidst at finde et instrument, der kan måle til tilstrækkeligt lavt q.

Hvis dine data har kvalitetsproblemer ved lavt q, som kan skyldes de ovenfor nævnte problemer, kan du finde ud af, at det kan forbedre kvaliteten af tilpasningen at udelukke disse data fra tilpasningen. Selv om dette kan være acceptabelt, bør du være forsigtig, når du gør det, og altid vise hele dataområdet på diagrammerne.Det mest acceptable tilfælde for dette er, at de første punkter enten er for høje eller for lave, men at resten af området passer perfekt (se nedenfor for kriterier for et godt fit). I så fald kan de par punkter, der er tættest på strålestoppet, have dårlig statistik eller højere instrumentel baggrundsspredning, og de kan normalt ignoreres uden risiko.