Løse hændelser, der finder sted i et kontinuerligt prøveområde, kan af mindst to grunde give anledning til geometriske billeder: på grund af problemets art eller på grund af løsningens art.

Visse problemer, som Buffons nål, Fugle på en tråd, Bertrands paradoks eller problemet med pinden, der er brudt i tre stykker, opstår i sagens natur i en geometrisk sammenhæng. Sidstnævnte problem tillader også flere omformuleringer, som kræver sammenligning af arealerne af geometriske figurer. Generelt kan vi tænke på geometriske sandsynligheder som ikke-negative størrelser (ikke over 1), der tildeles delområder af et givet område efter visse regler. Hvis funktionen μ er et udtryk for denne tildeling defineret på et domæne D, kræver vi f.eks.

0 ≤ μ(A) ≤ 1, A ⊂ D og
μ(D) = 1

Funktionen μ er normalt ikke defineret for alle A ⊂ D. De delmængder af D, for hvilke μ er defineret, er de tilfældige hændelser, der udgør et bestemt prøveområde. Meget ofte defineres μ ved hjælp af forholdet mellem arealer, således at hvis σ(A) defineres som “arealet” af mængden A, kan man sætte μ(A) = σ(A) / σ(D).

Problem 1

To venner, der tager metro til deres arbejde fra den samme station, ankommer til stationen ensartet tilfældigt mellem kl. 7 og 7:20 om morgenen. De er villige til at vente på hinanden i 5 minutter, hvorefter de tager et tog, enten sammen eller alene. Hvad er sandsynligheden for, at de mødes på stationen?

I et kartesisk koordinatsystem (s, t) repræsenterer et kvadrat med siden 20 (minutter) alle mulighederne for de to venners ankomst om morgenen til metrostationen.

Det grå område A er afgrænset af to rette linjer, t = s + 5 og t = s – 5, således at inden for A er |s – t| ≤ 5. Det følger heraf, at de to venner kun vil mødes, hvis deres ankomster s og t falder i område A. Sandsynligheden for, at dette sker, er givet ved forholdet mellem arealet af A og arealet af kvadratet:

/ 400 = 175/400 = 7/16.

Problem 2

(.)

Tre punkter A, B, C placeres tilfældigt på en cirkel med radius 1. Hvad er sandsynligheden for, at ΔABC er spids?.

Fiksér punkt C. Punkt A’s og B’s positioner defineres derefter af buer α og β, der strækker sig fra C i to retninger. A priori ved vi, at 0 < α + β < 2π. De for vores problem gunstige værdier af α og β (som subtenderende spidse vinkler opfylder) 0 < α < π og 0 < β < π. Deres sum kan ikke være mindre end π, da det ville gøre vinkel C stump, og derfor er α + β > π. Situationen er præsenteret i følgende diagram, hvor kvadratet har siden 2π.

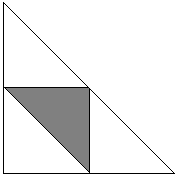
Region D er skæringspunktet mellem tre halvplaner: 0 < α, 0 < β og α + β < 2π. Dette er den store trekant i ovenstående diagram. De gunstige begivenheder hører til den skraverede trekant, som er skæringspunktet mellem halvplanerne α < π, β < π, og α + β > π. Forholdet mellem arealerne af de to er naturligvis 1/4.

Opmærk nu, at medmindre den tilfældige trekant er spids, kan den tænkes at være stump, da sandsynligheden for at to af de tre punkter A, B, C danner en diameter er 0. (For at BC skulle være en diameter, skulle man have α + β = π, hvilket er en ret linje, med nul som eneste mulige tildeling af areal). Vi kan således sige, at sandsynligheden for, at ΔABC er stumpet, er 3/4. For en stumpvinklet trekant kan cirklen deles i to halvdele, hvor trekanten ligger helt i den ene halvdel. Heraf følger, at 3/4 er svaret på følgende spørgsmål:

Tre punkter A, B, C er tilfældigt placeret på en cirkel med radius 1. Hvor stor er sandsynligheden for, at de alle tre ligger i en halvcirkel?

1. E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges by (MAA, 1995, problem 244.)
2. D. A. Klain, G.-C. Rota Introduction to Geometric Probability , Cambridge University Press, 1997
3. A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions, Dover, 1978
4. A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Geometric Probability

• Geometric Probabilities
• Are Most Triangles Obtuse?
  • Otte valg i seks sektorer
  • Tre tilfældige punkter på en cirkel
• Geometrisk sandsynlighed
  • Stav, der er brudt i tre stykker (trilineære koordinater)
  • Stav, der er brudt i tre stykker. Løsning i kartesiske koordinater
• Bertrands paradoks
• Fugle på en tråd (problem og interaktiv simulering)
  • Fugle på en tråd: Løsning af Nathan Bowler
  • Birds on a Wire. Løsning af Mark Huber
  • Birds on a Wire: en probabilistisk simulation. Løsning af Moshe Eliner
  • Birds on a Wire. Løsning af Stuart Anderson
  • Birds on a Wire. Løsning af Bogdan Lataianu
• Buffon’s Noodle Simulation
• Averaging Raindrops – an exercise in geometric probability
  • Averaging Raindrops, Part 2
• Rectangle on a Chessboard: en introduktion
• Mærkning og brydning af pinde
• Udsædvanlige punkter på et segment
• Semicirkeldækning
• Dækning af halvkugler
• Overlappende tilfældige intervaller
• Udsædvanlige intervaller
• med én dominerende
• Punkter på et kvadratisk gitter
• Flette sandsynligheder på en kugle
• Sandsynlighed i en trekant

|Kontakt|||Forside||Indhold|Op|

Copyright © 1996-2018 Alexander Bogomolny