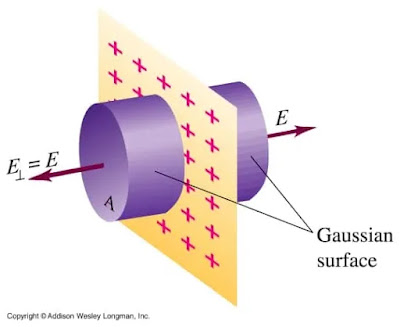
Når det drejer sig om elektrisk ladning og felt ved vi næsten alt om det, men hvad med Gauss-loven? Gauss-loven er et vigtigt emne i dette kapitel, men før vi går ind på Gauss-loven, skal vi forstå, hvad en Gauss-overflade er, og hvordan man bestemmer en Gauss-overflade?
Hvor vi går videre med, hvordan man bestemmer en Gauss-overflade, skal vi først forstå, hvad en Gauss-overflade er.

Hvad er en Gaussisk overflade?

Overflade, hvor vinklen (ө) mellem det elektriske felt (E) og arealvektoren (A) altid er konstant i hvert enkelt punkt, er denne form for overflade kendt som Gaussisk overflade.
Måske har du ikke forstået udtrykket elektrisk felt eller arealvektor. Så for at vide om elektrisk felt har jeg en dedikeret artikel om elektrisk ladning og felt, så læs også.
Vi ved, at vektormængde har størrelse og retning, derfor er arealvektorer vektor af plan overflade, hvis størrelse er arealet af overfladen, og retningen er vinkelret på overfladen.

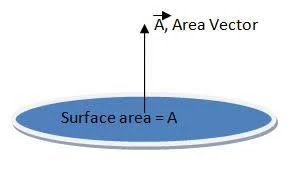
Arealvektor

Hvordan vil du identificere en Gaussisk overflade, hvis du ser en?

Hvordan bestemmer man en gaussisk overflade?

Vi ved, at gaussisk overflade følger Gauss-loven, og vinklen (ө) mellem det elektriske felt (E) og arealvektoren (A) er altid den samme i hvert punkt. Så for at bestemme en gaussisk overflade skal vi blot kontrollere, om vinklen (ө) i hvert punkt på en overflade er den samme eller ej.
Gauss-loven:

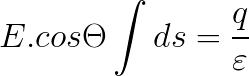
Her er trinene til bestemmelse af en gaussisk overflade:
Strin 1: Vælg overfladen fra et legeme eller objekt
Så ofte bliver folk forvirrede og begynder at kontrollere, om vinklen er den samme for alle punkter på et legeme eller ej. Det, du skal være klar over, er, at vi ønsker at identificere, om en overflade på et legeme er en gaussisk overflade eller ej, og derfor skal vi kontrollere vinklen (ө) i hvert punkt på overfladen og ikke i hvert enkelt punkt på hele legemet.

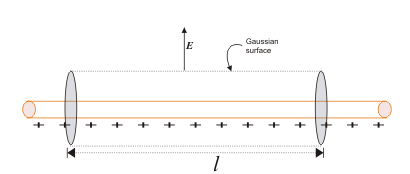
Identificering af en overflade

I ovenstående billede overvejer vi ikke-skygget område for at finde ud af, om det er en Gaussisk overflade eller ej, og skygget område er ikke overvejet, fordi vi skal finde ud af, om en overflade i et objekt er en Gaussisk overflade eller ej.
P.s: Det betyder, at et legeme kan have mere end 1 Gaussisk overflade.
Strin 2: Kontroller retning af elektrisk felt (E)
Nu efter at have bestemt overfladen skal du kontrollere retningen af det elektriske felt fra overfladen.
Hvorfra de elektriske feltlinjer går ud på en overflade.

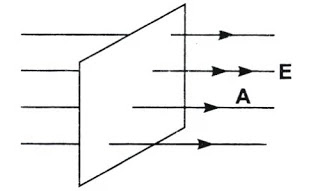
Retning af elektrisk felt

Hvis du ikke ved noget om elektrisk felt eller elektriske feltlinjer har vi en anden artikel om dette, så læs den også, for vi har også givet håndskrevne noter med hver afledning af elektrisk felt og Gaussisk overflade og lov også. Klik her for at læse den artikkel
Stræk 3: Kontroller arealvektoren (A)
Når du har kontrolleret det elektriske felts retning, skal du kontrollere arealvektoren for overfladen. Arealvektoren er faktisk en vektor, hvis retning altid er vinkelret på overfladen.
Stræk 4: Kontroller vinklen mellem arealvektoren (A) og det elektriske felt (E)
Så efter at have bestemt retningen af det elektriske felt og arealvektoren er det nu tid til at finde ud af vinklen (ө) mellem dem.

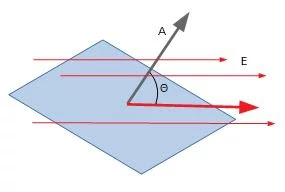
Vinkel mellem arealvektor og elektrisk felt

Kontroller, om vinklen mellem dem begge er den samme i alle punkter. Hvis Ja! så er det en Gaussisk overflade.

Ja, et spørgsmål som måske har slået dig er hvorfor er det nødvendigt at bestemme en Gaussisk overflade hvorfor er det så vigtigt?

Hvorfor er det nødvendigt at bestemme en Gaussisk overflade og hvordan hjælper det os?

Gaussisk overflade hjælper os med at vurdere elektrisk felt på grund af forskellig ladningsfordeling.
Hvis du ønsker at finde om vurdering af elektrisk felt på grund af forskellig ladningsfordeling har jeg mine personlige noter uploadet på dette site. Klik her for at gå til artiklen for at downloade noter.

Nogle eksempler på Gaussisk overflade:

Så nogle af eksemplerne på Gaussisk overflade er:
1. Imaginær cylindrisk gaussisk overflade skabt for at finde ud af det elektriske felt på grund af en lige ladet leder. Du kan også finde denne afledning i vores noter 🙂

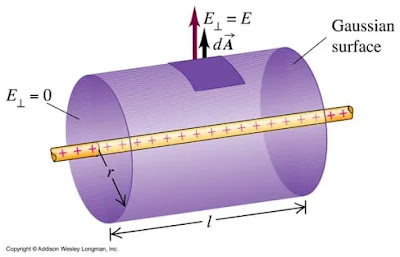
2. Imaginær cylindrisk gaussisk overflade skabt for at finde ud af det elektriske felt på grund af en plan ladet plade. Du vil også finde denne afledning i vores noter 🙂