Nul er et tal, der ligger lige mellem de positive og negative tal på tallinjen. Nul betragtes som et heltal sammen med de positive naturlige tal (1, 2, 3, 4…) og de negative tal, (…-4,-3,-2,-1).

Nul er et særligt tal i de hele tal, da det er det eneste hele tal, der hverken er positivt eller negativt. Det er også det eneste heltal, der hverken er et primtal eller et sammensat tal. Det betragtes som et lige tal, fordi det er deleligt med 2 uden rest. Nul er det additive identitetselement i forskellige algebra-systemer, og cifferet “0” bruges som en pladsholderværdi i positionelle notationssystemer til repræsentation af tal.

Nul har mange interessante egenskaber, der gør det interessant for matematikere. Hvis man adderer eller trækker nul fra et hvilket som helst tal, forbliver tallet det samme Hvis man ganger 0 med et hvilket som helst tal, er resultatet 0. Ethvert tal, der er hævet til den niende (0.) potens, er 1, så 20=1 og 560=1. I traditionel algebra er division med 0 udefineret, så intet tal kan divideres med 0. Tallet 0 er også et element i de reelle tal og de komplekse tal.

Historie om tallet 0

Hvor kom ideen om nul fra? I dag virker det intuitivt for os; nul er et tal, der står for en nulmængde – et ingenting. Vi ser nuller overalt i samfundet, og vi forstår naturligvis, hvad de betyder, og hvordan de kan manipuleres matematisk. Historisk set tog det dog lang tid, før begrebet 0 blev universelt anerkendt som et objekt i matematikken, og mange gennem historien har hævdet, at tallet nul ikke eksisterer, eller at ideen nul er et usammenhængende begreb.

Mange gamle samfund havde ikke et eksplicit begreb om mængden nul eller et specifikt tal til at bruge til at repræsentere det. De gamle egyptere og babyloniere havde begge en vis idé om en nulmængde og et behov for pladsholderværdier i repræsentationen af tal, men de udviklede aldrig et særskilt ciffer eller begreb til at repræsentere denne mængde eller pladsholderværdi. De gamle egyptiske talsystemer var udelukkende billedlige og havde ikke positionsværdier, mens de gamle babyloniere brugte mellemrum mellem tallene til at repræsentere positionsværdier.

Mayaerne havde et eksplicit begreb om 0 og havde et særskilt ciffer til at repræsentere begrebet og bruge som en pladsholderværdi i deres vigesimale (base-20) kalendersystem. Mens mayaerne, olmekerne og andre prækolombianske samfund var blandt de første i historien, der havde en eksplicit og sofistikeret forståelse af tallet 0, kom disse systemer ikke til at påvirke den gamle verdens samfund i Europa.

De gamle grækere havde på den anden side et kompliceret forhold til tallet 0. De havde ikke et symbol for dets begreb eller for det som en stedfortræderværdi, fordi de var usikre på, om tallet 0 kunne betragtes som en ægte eksisterende ting. Hvordan, spurgte de, kunne noget (et tal) være ingenting (nul)? For grækerne var de naturlige tal (1, 2, 3, 4, …) afledt af vores forståelse af diskrete individuelle objekter i verden. Aristoteles selv argumenterede som bekendt for, at 0 ikke eksisterer med den begrundelse, at 0 repræsenterer et tomrum eller ingenting, og et ægte tomrum eller ingenting kan ikke eksistere.

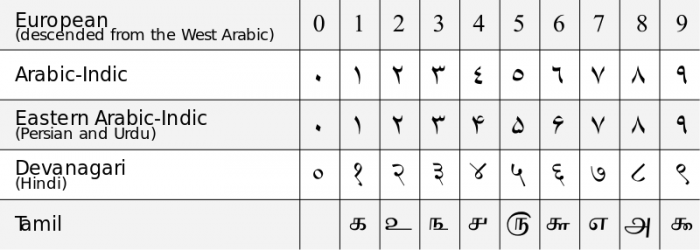
Kineserne havde en forståelse af “0” som et stedholderciffer i deres tællesystemer, men de anså ikke cifferet “0” for at repræsentere et bestemt tal, men kun et nyttigt symbol. Den almindelige forståelse af 0 som et særskilt tal og som et ciffer for positionelle notationssystemer kom fra Indien i løbet af det 6. århundrede e.Kr. De indiske matematikere på det tidspunkt udviklede de første former for decimale (base 10) notationssystemer, der indarbejdede 0 som et særskilt ciffer og havde en forståelse af nuls unikke matematiske egenskaber. I det 11. århundrede e.Kr. havde idéen om nul spredt sig til Vesteuropa via indflydelsen fra islamiske matematikere, der levede i Spanien under Umayyad-kalifatet, og det moderne arabiske talsystem med decimal notation blev skabt. Den første brug af det engelske ord “zero” stammer fra 1589.

Matematiske egenskaber ved nul

Tallet nul spiller en integreret rolle inden for næsten alle områder af matematikken. Nul er det mindste ikke-negative hele tal og har intet naturligt tal, der går forud for det. Da 0 er et heltal, er det også et rationelt tal, et reelt tal og et komplekst tal. I matematikken betragtes 0 som en størrelse, der svarer til en nulmængde. Man kan sige, at nul er den “mængde”, som besiddes af en mængde, der ikke har nogen medlemmer.

I algebra

I elementær algebra udtrykkes nul ofte som liggende i midten af tallinjen. Tallet 0 betragtes som et lige tal, da det er et heltalsmultipel af tallet 2 (2×0=0=0). 0 er ikke et primtal, fordi det har uendeligt mange faktorer, og det er ikke et sammensat tal, fordi intet produkt af to primtal er lig med tallet 0.

Med hensyn til de 4 aritmetiske hovedoperatorer (+, -, ×, ÷) og eksponentoperationen opfører tallet 0 sig efter følgende regler:

• Addition: x+0=0=0+x=x. Nul betragtes som det additive identitetselement, da ethvert tal plus eller minus nul er lig med dette tal
• Subtraktion: x-0=x og 0-x=-x
• Multiplikation: x⋅0=0=0⋅x=0. Ethvert tal gange 0 er også lig med 0.
• Division: 0/x=0, undtagen når x=0. x/0 er en matematisk udefineret størrelse, da 0 ikke har nogen multiplikativ omvendt størrelse (intet tal gange 0 giver 1).
• Exponenter: x0=1, undtagen når x=0. Der har længe været diskussion om, hvorvidt 00 er udefineret eller et velformet udtryk. For alle positive x gælder 0x=0.

I udtryk, der involverer grænser, kan mængden 0/0 dukke op i forbindelse med at demonstrere grænser for rationale funktioner som f(x)/g(x). I disse tilfælde er 0/0 ikke udefineret, men repræsenterer en ubestemt form. Det betyder ikke, at grænsen er udefineret, men at den skal beregnes ved hjælp af en anden metode, f.eks. ved at finde derivater. Der findes nogle algebraiske modeller, hvor division med nul giver en defineret størrelse, f.eks. den projektivt udvidede reelle linje eller Riemann-sfæren.

I mængdelære

I mængdelære svarer tallet 0 til kardinaliteten den “tomme mængde” eller “nulmængden” (almindeligvis repræsenteret som {} eller {∅}. En mængdes kardinalitet er mængden af elementer i den pågældende mængde, hvis man ikke har nogen appelsiner, har man en mængde med 0 appelsiner (en tom mængde appelsiner).

Zero bruges ofte som udgangspunkt i mængdelæren til at konstruere resten af de naturlige tal. Disse von Neumman-konstruktioner, der er opkaldt efter den berømte polymat John von Neumann, konstruerer de naturlige tal ved at definere 0={} og definerer en efterfølgerfunktion S(a) = a ∪ {a}. Alle de naturlige tal kan konstrueres ud fra de rekursive anvendelser af efterfølgerfunktionen, der begynder med det tomme sæt:

0 = {}

1 = 0 ∪ {0} = {0} = {{}}

2 = 1 ∪ {1} = {0,1} = {{}, {{}}}}

3 = 2 ∪ {2} = {0, 1, 2} = {{}, {{}}, {{}, {{}, {{}}}}

og så videre. Hvis man følger dette mønster, kan man konstruere hele den uendelige mængde af de naturlige tal. På denne måde kan man sige, at hvert naturligt tal svarer til den mængde, der indeholder alle de naturlige tal før det.

I fysik

I forbindelse med at foretage kvantitative målinger i fysik anses 0 for at være den grundlinje, hvorfra alle andre målinger af enheder foretages. Meget ofte svarer basislinjen 0 til en eller anden fysisk betydningsfuld variabel, der naturligt kan skelnes fra alle andre størrelser af målinger.

For eksempel svarer en temperatur på 0 K på Kelvinskalaen til absolut 0- den koldeste temperatur, der er fysisk mulig. I Celsius-skalaen er 0 °C defineret som vands frysepunkt ved atmosfærisk tryk. I forbindelse med dynamik og elektromagnetisme gives en værdi på 0 til den position, hvor et system har den mindst mulige mængde potentiel energi. F.eks. tildeles et atoms grundtilstand, det lavest mulige energiniveau for atomets elektroner, ofte en værdi på 0.

Det samme gælder i forbindelse med kinematik, hvor den referenceramme, hvorfra bevægelsesobservationer foretages, defineres som havende et midtpunkt, der ligger på koordinataksens oprindelse i punktet (0, 0). I tilfælde af bevarede størrelser, som masse-energi, impuls og vinkelmoment, er den samlede ændring af de bevarede størrelser i et isoleret system altid lig med 0.

I datalogi

Computere lagrer information i form af bits-lange sekvenser af 1’er og 0’er. I denne binære repræsentation svarer 0 til en “slukket” position og står i kontrast til den “tændte” position, der betegnes med 1. En værdi på 0 på et elektrisk kredsløb betyder, at kredsløbet er slukket og ikke har nogen elektrisk strøm. På samme måde definerer mange beregningslogikker “0” som det tegn, der repræsenterer en falsk sandhedsværdi.

I computerdatabaser tælles elementerne i et array ved hjælp af et nulbaseret tællesystem. Det betyder, at for et sæt med n elementer har elementerne indekser, der starter med 0. Således er et element med indeksnummer 0 faktisk det første element i rækken, og et indeksnummer 1 svarer til det andet element osv. Generelt har den niende term i en mængde et indeksnummer svarende til n-1. Dette tællesystem kan skabe forvirring hos nye programmører, som er vant til intuitivt at tildele indeksværdier, der begynder med 1.