Hvor meget ved du om uendelighed? Du har sikkert hørt om et tal, der er det størst mulige tal eller umuligt stort.
For at forklare uendelighed er jeg først nødt til at definere noget terminologi.
Intaller er tal, der bruges til at tælle. Mængden af hele tal er defineret som alle tal uden brøkdele. Nogle eksempler er: Der er f.eks. eksempler: -12, 0, 1, 3, 42, 17.
Uendelighed er begrebet om et objekt, der ligger uden for de naturlige tals rækkevidde. Det blev først konceptualiseret af en russisk matematiker ved navn Georg Cantor, som ikke blot introducerede uendelighed, men også afslørede, at der eksisterede flere uendeligheder.
Cantor leverede et kontroversielt bevis for uendelighed, som sagde, at nogle uendeligheder var større end andre. I første omgang kan dette virke umuligt – hvordan kan et objekt være større end et andet objekt, der er uendeligt?

Cantor baserede sit bevis på en gren af matematikken, der tilsyneladende er ubrugelig: mængdelære. En mængde er en samling af objekter – for eksempel kan vi have en mængde, der indeholder 1, 2 og 3. Disse objekter i mængden kaldes elementer.
I matematisk notation ville det se sådan ud:
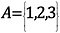
Antal af elementer i denne mængde, eller mængdens kardinalitet, er 3.
Dette betegnes som:
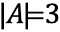
Hvis vi nu har en anden mængde, B, der indeholder objekter, således at
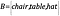
Hvordan kan vi vide, at mængderne har samme størrelse?
En måde, vi kan se det på, er ved at tælle antallet af elementer i den anden mængde. Vi kan tydeligt se, at denne mængde også har 3 elementer i den, og derfor ved vi, at de har samme størrelse.
En anden måde, vi kan gøre det på, er ved at sammenligne vores anden mængde, B, med vores første mængde, A, ved at mappe.
Vi kan mappe det første element fra mængde A , 1, til det første element i mængde B, stol.
Vi kan mappe det andet element fra mængden A, 2, til det andet element i mængden B, bord.
Vi kan mappe det tredje element fra mængden A, 3, til det tredje element i mængden B, hat.
Da hvert element fra A er mappet på præcis 1 element fra B, har mængderne samme størrelse.
Lad os nu tage et kig på uendelige mængder. Mængden af hele tal, som blev nævnt i begyndelsen, er en uendelig mængde – der findes et uendeligt antal hele tal. Mængden af hele tal betegnes med symbolet
Mængden af lige tal, som vi kan betegne som

er defineret som
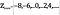
Intuitivt, kan det se ud som
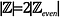
som der er 2 hele tal for hvert lige hele tal: 1 ulige heltal og 1 lige heltal. Lad os verificere dette.
Lad os prøve at sammenligne mængderne ved at mappe elementer fra 1 mængde til den anden.
Vi kan mappe 1 til 2, 2 til 4, 3 til 6 og så videre.
Hvis dette fortsætter i alle mængderne, kan vi se, at hvert element fra heltalsmængden kortlægger på præcis 1 element fra den lige heltalsmængde.
Sådan er mængderne lige store, selv om det kan virke kontraintuitivt.