La varianza es un número que indica la distancia que hay entre un conjunto de números.La varianza es idéntica a la desviación estándar al cuadrado y, por tanto, expresa «lo mismo» (pero con más fuerza).
Varianza – Ejemplo
Un estudio hace que 100 personas realicen una tarea de velocidad simple durante 80 ensayos. Así, para cada participante se registran 80 tiempos de reacción (en segundos). Parte de estos datos se muestran a continuación.

En estudios como éste, normalmente vemos que las personas son más rápidas a medida que realizan la tarea de velocidad con más frecuencia. Es decir, el tiempo de reacción medio tiende a disminuir a lo largo de los ensayos.
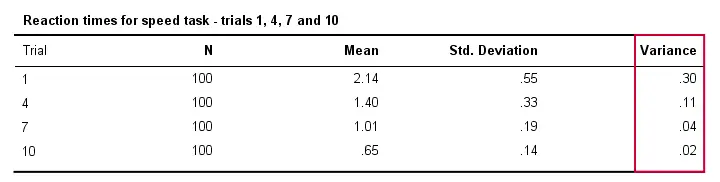
Además, los tiempos de reacción suelen variar menos entre diferentes personas en la medida en que realizan la tarea con más frecuencia. Técnicamente, decimos que la varianza disminuye a lo largo de los ensayos. La siguiente tabla ilustra esto para los ensayos 1,4,7 y 10.
Varianza e Histograma
Una gran manera de visualizar los datos de nuestra tabla anterior es un histograma para cada ensayo. Así, la figura de abajo ilustra que los participantes fueron más rápidos a lo largo de los ensayos; desde el ensayo 1 hasta el ensayo 10 las barras del histograma se mueven hacia la izquierda, hacia 0 segundos.
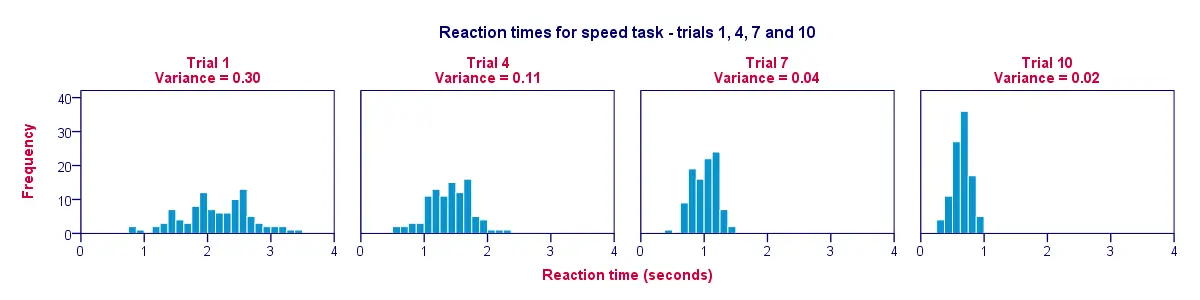
Un segundo hallazgo es que los histogramas se vuelven más estrechos (y por lo tanto más altos) a medida que nos movemos del ensayo 1 al ensayo 10; esto ilustra que los tiempos de reacción varían cada vez menos entre nuestros participantes a medida que el experimento progresa. La varianza disminuye a lo largo de los ensayos.
Varianza – Fórmula poblacional
Una fórmula básica para calcular la varianza es
$$S^2 = \frac{{suma(X – \overline{X})^2}{n}$
Le recomendamos que intente entender lo que hace esta fórmula porque esto ayuda mucho a entender el ANOVA (= análisis de la varianza). Por lo tanto, lo demostraremos en un mero puñado de datos.
Varianza – GoogleSheets
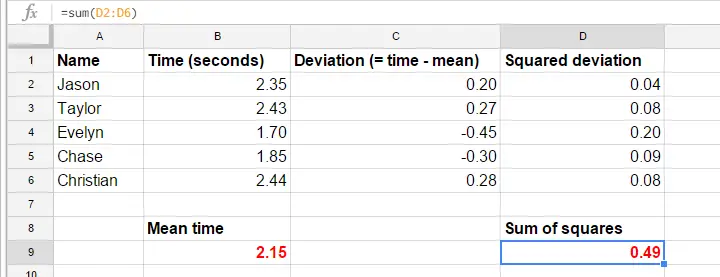
Para simplificar, recortaremos nuestros datos al primer ensayo de los 5 primeros participantes. Estos 5 tiempos de reacción -y un cálculo manual de su varianza- están en esta GoogleSheet.
Varianza – Pasos de cálculo
Las fórmulas en la GoogleSheet muestran precisamente cómo calcular una varianza. Los pasos básicos son
- calcular el tiempo de reacción medio (2,15);
- calcular las puntuaciones de desviación (tiempo de reacción menos tiempo de reacción medio);
- calcular las puntuaciones de desviación al cuadrado;
- sumar las puntuaciones de desviación al cuadrado. El resultado (0,49) es una suma de cuadrados, el bloque principal de ANOVA;
- dividir la suma de cuadrados por el número de observaciones (5 tiempos de reacción).
Alternativamente, calcular una varianza escribiendo =VARP(B2:B6) en alguna celda (B2:B6 son las celdas que contienen nuestros 5 tiempos de reacción). VARP es la abreviatura de «población de varianza». OpenOffice y MS Excel contienen fórmulas similares.
Varianza – Fórmula de la muestra
De forma similar a la desviación estándar, si nuestros datos son una simple muestra aleatoria de una población mucho mayor, la fórmula mencionada subestimará sistemáticamente la varianza de la población. En este caso, utilizaremos una fórmula ligeramente diferente:
$$S^2 = \frac{{suma(X_i – \overline{X})^2}{n – 1}$
La fórmula a utilizar depende, por tanto, de nuestros datos: ¿contienen toda la población que queremos investigar o son una mera muestra de esta población?
Como nuestros 100 participantes son claramente una muestra, utilizaremos la fórmula de la muestra. En GoogleSheets, si escribimos =VAR(B2:B6) en alguna celda obtendremos la varianza de la muestra.
Varianza en SPSS
Por lo que sabemos, la fórmula para la varianza de la población está completamente ausente en SPSS y lo consideramos un grave defecto. En su lugar, SPSS siempre utiliza la fórmula de la muestra, tanto para la varianza entre sujetos (discutida en este tutorial) como para la varianza dentro de los sujetos. La salida relevante se muestra a continuación.

Respecto a esta tabla de salida, observe también que la varianza es efectivamente la desviación estándar al cuadrado (aparte del redondeo).
Respecto a la varianza, eso es todo. Esperamos que haya encontrado este tutorial útil para entender lo que es una varianza.