¿Cuánto sabes de infinitos? Probablemente hayas oído hablar de un número que es el mayor número posible, o imposiblemente grande.
Para explicar los infinitos, primero tengo que definir algo de terminología.
Los números enteros son números que se utilizan para contar. El conjunto de los enteros se define como todos los números sin componentes fraccionarios. Algunos ejemplos son: -12, 0, 1, 3, 42, 17.
El infinito es el concepto de un objeto más allá del alcance de los números naturales. Fue conceptualizado por primera vez por un matemático ruso llamado Georg Cantor, quien no sólo introdujo el infinito, sino que también reveló que había múltiples infinitos que existían.
Cantor proporcionó una controvertida prueba de infinitos, que decía que algunos infinitos eran más grandes que otros. Al principio, esto puede parecer imposible -¿cómo puede un objeto ser más grande que otro objeto que es infinito?

Cantor basó su prueba en una rama de las Matemáticas aparentemente inútil: La teoría de conjuntos. Un conjunto es una colección de objetos -por ejemplo, podemos tener un conjunto que contenga 1, 2 y 3-. Estos objetos del conjunto se llaman elementos.
En notación matemática, esto se vería así:
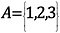
El número de elementos de este conjunto, o la Cardinalidad del conjunto, es 3.
Esto se denota como:
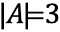
Si ahora tenemos otro conjunto, B, que contiene objetos, tal que
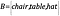
¿Cómo sabemos que los conjuntos tienen el mismo tamaño?
Una forma de verlo es contando el número de elementos del segundo conjunto. Podemos ver claramente que este conjunto también tiene 3 elementos, y así sabemos que tienen el mismo tamaño.
Otra forma de hacerlo es comparando nuestro segundo conjunto, B, con nuestro primer conjunto, A mediante un mapeo.
Podemos mapear el primer elemento del conjunto A , 1, con el primer elemento del conjunto B, silla.
Podemos mapear el segundo elemento del conjunto A, 2, al segundo elemento del conjunto B, mesa.
Podemos mapear el tercer elemento del conjunto A, 3, al tercer elemento del conjunto B, sombrero.
Como cada elemento de A se mapea en exactamente 1 elemento de B, los conjuntos tienen el mismo tamaño.
Veamos ahora los conjuntos infinitos. El conjunto de los números enteros, que se mencionó al principio, es un conjunto infinito: hay un número infinito de números enteros. El conjunto de los enteros se denota con el símbolo
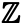
El conjunto de los números pares, que podemos denotar como

se define como
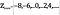
Intuitivamente, puede parecer que
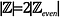
como hay 2 enteros por cada entero par: 1 entero impar y 1 entero par. Verifiquemos esto.
Intentemos comparar los conjuntos mapeando elementos de 1 conjunto a otro.
Podemos mapear 1 a 2, 2 a 4, 3 a 6, y así sucesivamente.
Si esto continúa a lo largo de los conjuntos, podemos ver que cada elemento del conjunto de enteros se asigna exactamente a 1 elemento del conjunto de enteros pares.
Así, aunque parezca contrario a la intuición, el tamaño de los conjuntos es igual.