El cero es un número que se encuentra entre los números positivos y negativos de la recta numérica. El cero se considera un número entero, junto con los números naturales positivos (1, 2, 3, 4…) y los números negativos, (…-4,-3,-2,-1).

El cero es un número especial en los enteros ya que es el único número entero que no es ni positivo ni negativo. También es el único número entero que no es ni primo ni compuesto. Se considera un número par porque es divisible por 2 sin resto. El cero es el elemento aditivo de identidad en varios sistemas de álgebra, y el dígito «0» se utiliza como valor marcador de posición en los sistemas de notación posicional para representar números.

El cero tiene muchas propiedades interesantes que lo hacen de interés para los matemáticos. Si se suma o se resta el cero a cualquier número, el número sigue siendo el mismo Si se multiplica el 0 por cualquier número, el resultado es 0. Cualquier número elevado a la potencia cero (0ª) es 1, por lo que 20=1 y 560=1. En el álgebra tradicional, la división por 0 no está definida, por lo que ningún número puede dividirse por 0. El número 0 es también un elemento de los números reales y de los números complejos.

Historia del número 0

¿De dónde viene la idea del cero? Hoy en día, nos parece intuitivo; el cero es un número que representa una cantidad nula, una nada. Vemos ceros por todas partes en la sociedad, y naturalmente entendemos lo que significan y cómo se pueden manipular matemáticamente. Sin embargo, históricamente, el concepto de 0 tardó bastante tiempo en ser reconocido universalmente como un objeto de las matemáticas, y muchos a lo largo de la historia argumentaron que el número cero no existe, o que la idea de cero es un concepto incoherente.

Muchas sociedades antiguas no tenían un concepto explícito de la cantidad de cero o un dígito específico para su representación. Tanto los antiguos egipcios como los babilonios tenían alguna idea de la cantidad nula y la necesidad de valores marcadores de posición en la representación de los números, pero nunca desarrollaron un dígito o concepto distinto para representar esa cantidad o valor marcador de posición. Los antiguos sistemas de numeración egipcios eran totalmente pictóricos y no tenían valores posicionales, mientras que los antiguos babilonios utilizaban espacios entre los números para representar valores posicionales.

Los mayas sí tenían un concepto explícito de 0 y tenían un dígito distinto para representar el concepto y utilizarlo como valor marcador de posición en su sistema de calendario vigesimal (base-20). Aunque los mayas, los olmecas y otras sociedades precolombinas fueron de las primeras en la historia en tener una comprensión explícita y sofisticada del número 0, estos sistemas no llegaron a influir en las sociedades del Viejo Mundo en Europa.

Los antiguos griegos, por otra parte, tenían una relación complicada con el cero. No tenían un símbolo para su concepto ni para él como valor de reserva porque no estaban seguros de que el número 0 pudiera considerarse una cosa genuinamente existente. ¿Cómo podía algo (un número) no ser nada (el cero)? Para los griegos, los números naturales (1, 2, 3, 4,…) se derivaban de nuestra comprensión de los objetos individuales discretos del mundo. El mismo Aristóteles argumentó que el 0 no existe, basándose en que el 0 representa un vacío o la nada, y un verdadero vacío o la nada no puede existir.

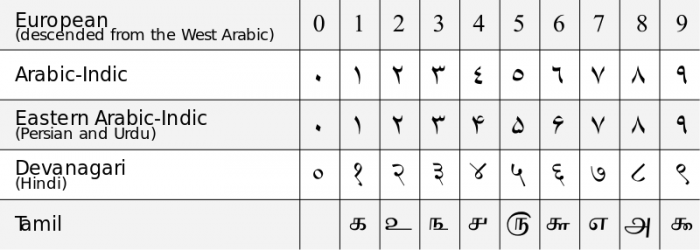
Los chinos entendían el «0» como un dígito marcador de posición para sus sistemas de conteo, pero no consideraban que el dígito «0» representara ningún número distinto, sólo un símbolo útil. La comprensión común del 0 como un número distinto y como un dígito para los sistemas de notación posicional vino de la India durante el siglo VI de nuestra era. Los matemáticos indios de la época desarrollaron los primeros tipos de sistemas de notación decimal (base 10) que incorporaban el 0 como un dígito distinto y comprendían las propiedades matemáticas únicas del cero. En el siglo XI d.C., la idea del cero se extendió a Europa occidental por influencia de los matemáticos islámicos que vivían en España bajo el califato omeya, y se creó el actual sistema numérico árabe de notación decimal. El primer uso de la palabra inglesa «zero» data de 1589.

Propiedades matemáticas del cero

El número cero juega un papel integral en casi todos los campos de las matemáticas. El cero es el número entero no negativo más pequeño y no tiene ningún número natural que lo preceda. Como el 0 es un número entero, también es un número racional, un número real y un número complejo. En matemáticas, el 0 se considera una cantidad que corresponde a una cantidad nula. Se podría decir que el cero es la «cantidad» que posee un conjunto que no tiene miembros.

En Álgebra

En el álgebra elemental, el cero se expresa a menudo como situado en el centro de la recta numérica. El número 0 se considera un número par ya que es un múltiplo entero del número 2 (2×0=0). El 0 no es un número primo porque tiene una cantidad infinita de factores, y no es un número compuesto porque ningún producto de dos números primos es igual al número 0.

Respecto a los 4 operadores aritméticos principales (+, -, ×, ÷) y a la operación de exponente, el número 0 se comporta según las siguientes reglas:

• Adición: x+0=0+x=x. El cero se considera el elemento aditivo identitario ya que cualquier número más o menos cero es igual a ese número
• Sustracción: x-0=x y 0-x=-x
• Multiplicación: x⋅0=0⋅x=0. Cualquier número por 0 es también igual a 0.
• División: 0/x=0, excepto cuando x=0. x/0 es una cantidad matemáticamente indefinida, ya que el 0 no tiene inverso multiplicativo (ningún número por 0 da 1).
• Exponentes: x0=1, excepto cuando x=0. Hace tiempo que se discute si 00 es indefinido o una expresión bien formada. Para todo x positivo, 0x=0.

En expresiones que implican límites, la cantidad 0/0 puede aparecer en el contexto de la demostración de límites de funciones racionales como f(x)/g(x). En estos casos, 0/0 no es indefinido sino que representa una forma indeterminada. Esto no significa que el límite sea indefinido, sino que debe calcularse mediante otro método, como la búsqueda de derivadas. Existen algunos modelos algebraicos en los que la división por cero da una cantidad definida, como la recta real proyectada o la esfera de Riemann.

En la teoría de conjuntos

En la teoría de conjuntos, el número 0 corresponde a la cardinalidad el «conjunto vacío» o el «conjunto nulo» (comúnmente representado como {} o {∅}. La cardinalidad de un conjunto es la cantidad de elementos de ese conjunto si no se tiene ninguna naranja, entonces se tiene un conjunto de 0 naranjas (un conjunto vacío de naranjas).

El cero se utiliza a menudo como punto de partida en la teoría de conjuntos para construir el resto de los números naturales. Estas construcciones de von Neumman, que llevan el nombre del renombrado polímata John von Neumann construyen los números naturales definiendo 0={} y definen una función sucesora S(a) = a ∪ {a}. La totalidad de los números naturales puede construirse a partir de las aplicaciones recursivas de la función sucesora empezando por el conjunto vacío:

0 = {}

1 = 0 ∪ {0} = {{}}

2 = 1 ∪ {1} = {0,1} = {{}, {{}}

3 = 2 ∪ {2} = {0, 1, 2} = {{}, {{}}, {{}}}}

y así sucesivamente. Siguiendo este patrón, se puede construir todo el conjunto infinito de los números naturales. De este modo, podemos decir que a cada número natural le corresponde el conjunto que contiene todos los números naturales anteriores a él.

En Física

En el contexto de la realización de medidas cuantitativas en física, se considera que el 0 es la línea de base a partir de la cual se realizan todas las demás medidas de unidades. Muy a menudo, la línea de base del 0 corresponde a alguna variable físicamente significativa que se distingue naturalmente de todas las demás magnitudes de medida.

Por ejemplo, en la escala Kelvin, una temperatura de 0 K corresponde al 0 absoluto- la temperatura más fría que es físicamente posible. En la escala de temperatura Celsius, 0 °C se define como el punto de congelación del agua a presiones atmosféricas. En el contexto de la dinámica y el electromagnetismo, se da el valor 0 a la posición en la que un sistema tiene la mínima cantidad posible de energía potencial. Por ejemplo, al estado básico de un átomo, el nivel de energía más bajo posible para los electrones del átomo, se le suele asignar un valor de 0.

Así mismo, en el contexto de la cinemática, el marco de referencia desde el que se realizan las observaciones del movimiento se define como el que tiene un punto central situado en el origen del eje de coordenadas en el punto (0, 0). En el caso de las cantidades conservadas, como la masa-energía, el momento y el momento angular, la cantidad total de cambio de las cantidades conservadas en un sistema aislado es siempre igual a 0.

En Ciencias de la Computación

Los ordenadores almacenan la información en forma de secuencias largas de bits de 1s y 0s. En esta representación binaria, el 0 corresponde a una posición de «apagado» y se contrapone a la posición de «encendido» designada por el 1. Un valor de 0 en un circuito eléctrico significa que el circuito está apagado y no tiene ningún flujo eléctrico. De forma similar, muchas lógicas computacionales definen el «0» como el carácter que representa un valor de verdad falso.

En las bases de datos informáticas, los elementos de una matriz se cuentan utilizando un sistema de recuento basado en el cero. Esto significa que para un conjunto con n elementos, los elementos tienen índices que empiezan por 0. Así, un elemento con un número de índice 0 es en realidad el primer elemento de la serie, y un número de índice 1 corresponde al segundo elemento, y así sucesivamente. En general, el enésimo término de un conjunto tiene un número de índice correspondiente a n-1. Este sistema de conteo puede causar confusión a los nuevos programadores que están acostumbrados a asignar intuitivamente valores de índice que comienzan por 1.