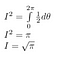Lord Kelvin escribió sobre esta integral: «Un matemático es aquel para quien esto es tan obvio como que dos veces dos son cuatro es para ti»
Disfruta 😉
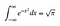
Bien, voy a suponer que sabes algo de integración y diferenciación básicas. Lo siguiente añadirá algo de intuición a los trucos inteligentes que vienen después. No te preocupes si algo de esto es un poco desconcertante, sólo trata de conseguir una sensación de lo que está sucediendo.
La estrategia aquí será hacer una sustitución inteligente. Pero haremos una sustitución en dos variables. Puedes visualizar el problema actual como el cálculo del área bajo una curva
Pero mostraremos que el problema puede convertirse en uno de cálculo de un volumen.
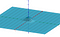
Para calcular el volumen, utilizamos una fórmula de cambio de variable ligeramente diferente a la que se utiliza en las integrales normales. Utilizaremos coordenadas polares. Esto expresa las coordenadas x e y en términos de su radio y su ángulo. Geogebra tiene una bonita forma interactiva de verlo aquí

Entonces usaremos la fórmula mágica de cambio de base para coordenadas polares.
Al calcular el área bajo la curva, teníamos el elemento ‘dx’ que representa una pequeña distancia a lo largo del eje x. Al calcular un volumen, tenemos dx dy, que es como un pequeño rectángulo con longitudes de lado dx y dy. A continuación, utilizamos estas bases para crear una serie de casillas que estiman el volumen. Esto es más fácil de ver con la siguiente visualización. La integral es el límite de estas aproximaciones.
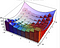
Cuando, en cambio, utilizamos el sistema de coordenadas polares, tenemos un elemento de área ligeramente diferente por debajo. Abajo, dA es el elemento de área. Con pequeños cambios en el ángulo y el radio, este elemento de área puede ser cada vez más bien aproximado por un rectángulo con longitudes de lado dr y r*dtheta respectivamente. Si te sientes cómodo con algo de geometría, para pequeños theta sin(theta) se aproxima muy bien por theta y entonces puedes probar el resultado de abajo.
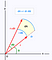
Resolución de la integral
Primero damos un nombre a nuestra integral. La llamamos I.
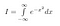
Nótese que x es sólo una ‘variable ficticia’. El área existe independientemente del nombre de la variable que utilicemos. Así que también podemos escribir las dos ecuaciones siguientes
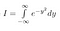
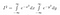
Ahora bien, como I es sólo una constante, aunque todavía no conocemos su valor, podemos usar nuestras reglas normales para meter una constante dentro de una integral
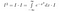
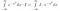
Hasta ahora no hemos hecho gran cosa. Ahora pensamos mucho en lo que significa la integral. Tomamos integrales de funciones. Si dos funciones toman el mismo valor en todas partes, son iguales y tienen la misma área. Con esto en mente, podemos hacer las siguientes manipulaciones, si vemos I*exp(-x²) como una función de x, es decir, algo que toma valores de x como entrada, y da un número como salida.
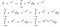
Ok, eso fue mucho para asimilar. En la primera línea, acabamos de reescribir I en su forma integral con un nombre de variable diferente. En la segunda línea, tratando I*exp(-x²) como una función, nos dimos cuenta de que podíamos meter la exp(-x²) dentro de la integral dy, y esto seguiría dando el mismo valor de salida para cualquier valor de entrada de x. Por último, utilizamos las reglas de la exponenciación.
Escribiendo esto en su totalidad, ahora tenemos
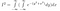
A continuación viene la idea asesina. Antes hemos jugado con los nombres de las variables y con la forma de representar una función. Ahora cambiamos de perspectiva: esta expresión también representa la integral de exp(-(y²+x²)) sobre todo el plano 2D, con el elemento de área dA = dx dy. Es decir, dx dy es un pequeño rectángulo en un plano, y exp(-(y²+x²)) es la altura sobre ese rectángulo.
A continuación, utilizamos las ideas de coordenadas polares de antes
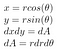
Como sin² + cos² = 1, después de enchufar todo, obtenemos
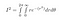
r va de 0 a infinito y theta va de 0 a 2*pi, porque esto cubre todo el plano 2D: cualquier punto tiene un radio menor que el infinito, y un ángulo entre 0 y 2pi radianes.
Podemos evaluar la integral interna utilizando la regla de la cadena
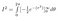
Y, en la tierra prometida nos encontramos ahora: