Definiciones de Estadística> Prueba de Friedman
¿Qué es la prueba de Friedman?
La prueba de Friedman es una prueba no paramétrica para encontrar diferencias en los tratamientos a través de múltiples intentos. No paramétrico significa que la prueba no asume que los datos provienen de una distribución particular (como la distribución normal). Básicamente, se utiliza en lugar de la prueba ANOVA cuando no se conoce la distribución de los datos.
La prueba de Friedman es una extensión de la prueba de signos, utilizada cuando hay múltiples tratamientos. De hecho, si sólo hay dos tratamientos las dos pruebas son idénticas.
Ejecución de la prueba
Sus datos deben cumplir los siguientes requisitos:
- Los datos deben ser ordinales (por ejemplo la escala de Likert) o continuos,
- Los datos proceden de un único grupo, medido en al menos tres ocasiones diferentes,
- La muestra se creó con un método de muestreo aleatorio,
- Los bloques son mutuamente independientes (es decir.es decir, todos los pares son independientes – uno no afecta al otro),
- Las observaciones se clasifican dentro de los bloques sin empates.
La hipótesis nula para la prueba es que todos los tratamientos tienen efectos idénticos, o que las muestras difieren de alguna manera. Por ejemplo, tienen centros, distribuciones o formas diferentes. La hipótesis alternativa es que los tratamientos tienen efectos diferentes.
Prepare sus datos para la prueba.
Paso 1: Ordene sus datos en bloques (columnas en una hoja de cálculo).Para este ejemplo, tenemos 12 pacientes que reciben tres tratamientos diferentes.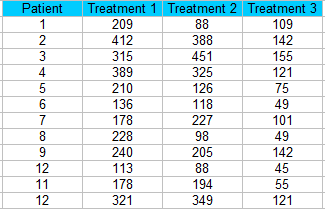
Paso 2: Clasifique cada columna por separado. La puntuación más pequeña debería obtener un rango de 1. Estoy clasificando a través de las filas aquí, así que cada paciente está siendo clasificado con un 1, 2 o 3 para cada tratamiento.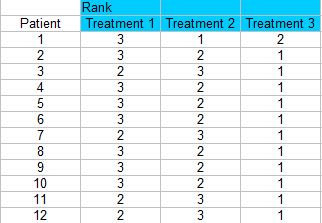
Paso 3: Sumar los rangos (encontrar un total para cada columna).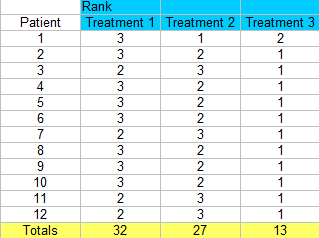
Ejecutar la prueba
Nota: Esta prueba no se suele realizar a mano, ya que los cálculos requieren mucho tiempo y trabajo. Casi todos los paquetes de software estadístico populares pueden ejecutar esta prueba. Sin embargo, incluyo aquí los pasos manuales como referencia.
Paso 4: Calcular la estadística de la prueba. Necesitará:
- n: el número de sujetos (12)
- k: el número de tratamientos (3)
- R: los rangos totales para cada una de las tres columnas (32, 27, 13).
Inserte estos datos en la siguiente fórmula y resuelva: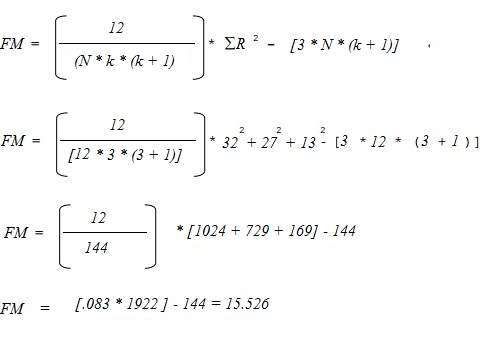
Paso 5: Encuentre el valor crítico de FM a partir de la tabla de valores críticos de Friedman (véase la tabla siguiente).
Utilice la tabla k=3 (ya que ese es el número de tratamientos que tenemos) y un nivel alfa del 5%. Podría elegir un nivel alfa más alto o más bajo, pero el 5% es bastante común, así que utilice la tabla del 5% si no conoce su nivel alfa.
Al buscar n-12 en esa tabla, encontramos un valor crítico de FM de 6,17.
Paso 6: Compare el estadístico de prueba de FM calculado (Paso 4) con el valor crítico de FM (Paso 5). Rechace la hipótesis nula si el valor F calculado es mayor que el valor crítico de FM.:
- Estadística de prueba de FM calculada = 15,526.
- Valor crítico de FM de la tabla = 6,17.
El estadístico FM calculado es mayor, por lo que se rechazaría la hipótesis nula.
Tabla de valores críticos del ANOVA de Friedman por rangos
Tres tablas según «k».
Si su k es superior a 5, o su n es superior a 13, utilice la tabla de valores críticos de chi cuadrado del paso 5 para obtener el valor crítico.
k=3
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 6,00 | 6,00 | – |
| 4 | 6.00 | 6.50 | 8.00 |
| 5 | 5.20 | 6.40 | 8.40 |
| 6 | 5.33 | 7.00 | 9.00 |
| 7 | 5.43 | 7.14 | 8.86 |
| 8 | 5.25 | 6.25 | 9.00 |
| 9 | 5.56 | 6.22 | 8.67 |
| 10 | 5.00 | 6.20 | 9.60 |
| 11 | 4.91 | 6.54 | 8.91 |
| 12 | 5.17 | 6.17 | 8.67 |
| 13 | 4.77 | 6,00 | 9,39 |
| ∞ | 4,61 | 5,99 | 9,21 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 2 | 6,00 | 6,00 | – |
| 3 | 6.60 | 7.40 | 8.60 |
| 4 | 6.30 | 7.80 | 9.60 |
| 5 | 6.36 | 7.80 | 9.96 |
| 6 | 6.40 | 7.60 | 10.00 |
| 7 | 6.26 | 7.80 | 10.37 |
| 8 | 6.30 | 7.50 | 10.35 |
| ∞ | 6.25 | 7.82 | 11.34 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 7.47 | 8.53 | 10.13 | 4 | 7.60 | 8.80 | 11.00 | 5 | 7.68 | 8.96 | 11.52 | ∞ | 7.78 | 9.49 | 13,28 |
Referencia:
Análisis de varianza de dos vías por rangos de Friedman – Análisis de datos k-dentro de un grupo con una
variable de respuesta cuantitativa. Recuperado el 7-17-2016 de: http://psych.unl.edu/psycrs/handcomp/hcfried.PDF
Stephanie Glen. «Prueba de Friedman / Análisis de varianza de dos vías por rangos» De StatisticsHowTo.com: ¡Estadística elemental para el resto de nosotros! https://www.statisticshowto.com/friedmans-test/
——————————————————————————
¿Necesitas ayuda con una tarea o pregunta de examen? Con Chegg Study, puede obtener soluciones paso a paso a sus preguntas de un experto en la materia. ¡Tus primeros 30 minutos con un tutor de Chegg son gratis!