Los sucesos aleatorios que tienen lugar en un espacio muestral continuo pueden invocar imágenes geométricas por al menos dos razones: debido a la naturaleza del problema o debido a la naturaleza de la solución.

Algunos problemas, como el de la aguja de Buffon, el de los pájaros en el cable, la paradoja de Bertrand o el problema del palo roto en tres trozos se plantean, por su naturaleza, en un entorno geométrico. Este último admite además múltiples reformulaciones que requieren la comparación de las áreas de las figuras geométricas. En general, podemos pensar en las probabilidades geométricas como cantidades no negativas (que no exceden de 1) que se asignan a subregiones de un dominio dado con arreglo a ciertas reglas. Si la función μ es una expresión de esta asignación definida sobre un dominio D, entonces, por ejemplo, requerimos

0 ≤ μ(A) ≤ 1, A ⊂ D y
μ(D) = 1

La función μ no suele estar definida para todos los A ⊂ D. Aquellos subconjuntos de D para los que μ está definida son los sucesos aleatorios que forman un determinado espacio muestral. Muy a menudo μ se define mediante el cociente de áreas, de modo que, si σ(A) se define como el «área» del conjunto A, entonces se puede establecer μ(A) = σ(A) / σ(D).

Problema 1

Dos amigos que cogen el metro para ir a sus trabajos desde la misma estación llegan a la estación uniformemente al azar entre las 7 y las 7:20 de la mañana. Están dispuestos a esperarse mutuamente durante 5 minutos, tras lo cual toman un tren ya sea juntos o solos. ¿Cuál es la probabilidad de que se encuentren en la estación?

En un sistema cartesiano de coordenadas (s, t), un cuadrado de lado 20 (minutos) representa todas las posibilidades de las llegadas matutinas de los dos amigos a la estación de metro.

La zona gris A está delimitada por dos rectas, t = s + 5 y t = s – 5, de modo que dentro de A, |s – t| ≤ 5. Se deduce que los dos amigos se encontrarán sólo si sus llegadas s y t caen dentro de la región A. La probabilidad de que esto ocurra viene dada por el cociente entre el área de A y el área del cuadrado:

/ 400 = 175/400 = 7/16.

Problema 2

(.)

Tres puntos A, B, C se sitúan al azar en un círculo de radio 1. Cuál es la probabilidad de que ΔABC sea agudo?.

Fijar el punto C. Las posiciones de los puntos A y B quedan entonces definidas por los arcos α y β que se extienden desde C en dos direcciones. A priori sabemos que 0 < α + β < 2π. Los valores favorables para nuestro problema de α y β (como ángulos agudos subtendidos satisfacen) 0 < α < π y 0 < β < π. Su suma no podría ser menor que π ya que esto haría que el ángulo C fuera obtuso, por tanto, α + β > π. La situación se presenta en el siguiente diagrama donde el cuadrado tiene el lado 2π.

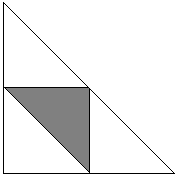
La región D es la intersección de tres semiplanos: 0 < α, 0 < β, y α + β < 2π. Este es el gran triángulo del diagrama anterior. Los sucesos favorables pertenecen al triángulo sombreado que es la intersección de los semiplanos α < π, β < π, y α + β > π. El cociente de las áreas de ambos es obviamente 1/4.

Obsérvese ahora, que a menos que el triángulo aleatorio sea agudo, puede pensarse que es obtuso, ya que la probabilidad de que dos de los tres puntos A, B, C formen un diámetro es 0. (Para que BC sea un diámetro, habría que tener α + β = π, que es una recta, con cero como única asignación posible de área). Así podemos decir que la probabilidad de que ΔABC sea obtuso es de 3/4. En el caso de un triángulo obtuso, el círculo se puede dividir en dos mitades y el triángulo se encuentra completamente en una de ellas. Se deduce que 3/4 es la respuesta a la siguiente pregunta:

Tres puntos A, B, C se colocan al azar en un círculo de radio 1. ¿Cuál es la probabilidad de que los tres se encuentren en un semicírculo?

1. E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges by (MAA, 1995, problema 244.)
2. D. A. Klain, G.-C. Rota Introduction to Geometric Probability , Cambridge University Press, 1997
3. A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions, Dover, 1978
4. A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Probabilidad geométrica

• Probabilidades geométricas
• ¿Son la mayoría de los triángulos obtusos?
  • Ocho selecciones en seis sectores
  • Tres puntos aleatorios en una circunferencia
• Probabilidad geométrica
  • Palo partido en tres trozos (coordenadas trilineales)
  • Palo partido en tres trozos. Solución en coordenadas cartesianas
• Paradoja de Bertrand
• Pájaros en un cable (problema y simulación interactiva)
  • Pájaros en un cable: Solución por Nathan Bowler
  • Birds on a Wire. Solución por Mark Huber
  • Birds on a Wire: una simulación probabilística. Solución por Moshe Eliner
  • Birds on a Wire. Solución por Stuart Anderson
  • Birds on a Wire. Solución por Bogdan Lataianu
• Simulación de fideos de Buffon
• Promediando gotas de lluvia – un ejercicio de probabilidad geométrica
  • Promediando gotas de lluvia, Parte 2
• Rectángulo en un tablero de ajedrez: una introducción
• Marcando y rompiendo palos
• Puntos aleatorios en un segmento
• Cobertura del semicírculo
• Cobertura de la semiesfera
• Intervalos aleatorios superpuestos
• Intervalos aleatorios con una dominante
• Puntos en una cuadrícula cuadrada
• Probabilidades planas en una esfera
• Probabilidad en triángulo

|Contacto||Página de entrada|||Contenido|

Copyright © 1996-2018 Alexander Bogomolny