La convolución no deseada es un problema inherente a la transferencia de información analógica. Por ejemplo, todo lo siguiente se puede modelar como una convolución: el desenfoque de la imagen en una cámara temblorosa, los ecos en las llamadas telefónicas de larga distancia, el ancho de banda infinito de los sensores analógicos y la electrónica, etc. La deconvolución es el proceso de filtrado de una señal para compensar una convolución no deseada. El objetivo de la deconvolución es recrear la señal tal y como era antes de la convolución. Para ello, suele ser necesario conocer las características de la convolución (es decir, la respuesta de impulso o de frecuencia). Esto puede distinguirse de la deconvolución ciega, en la que no se conocen las características de la convolución parásita. La deconvolución ciega es un problema mucho más difícil que no tiene una solución general, y el enfoque debe adaptarse a la aplicación particular.

La deconvolución es casi imposible de entender en el dominio del tiempo, pero es bastante sencilla en el dominio de la frecuencia. Cada sinusoide que compone la señal original puede cambiar de amplitud y/o fase al pasar por la convolución no deseada. Para extraer la señal original, el filtro de deconvolución debe deshacer estos cambios de amplitud y fase. Por ejemplo, si la convolución cambia la amplitud de una sinusoide en 0,5 con un cambio de fase de 30 grados, el filtro de deconvolución debe amplificar la sinusoide en 2,0 con un cambio de fase de -30 grados.

El ejemplo que usaremos para ilustrar la deconvolución es un detector de rayos gamma. Como se ilustra en la Fig. 17-3, este dispositivo está compuesto por dos partes, un centelleador y un detector de luz. Un centelleador es un tipo especial de material transparente, como el yoduro de sodio o el germanato de bismuto. Estos compuestos transforman la energía de cada rayo gamma en una breve ráfaga de luz visible. Esta luz

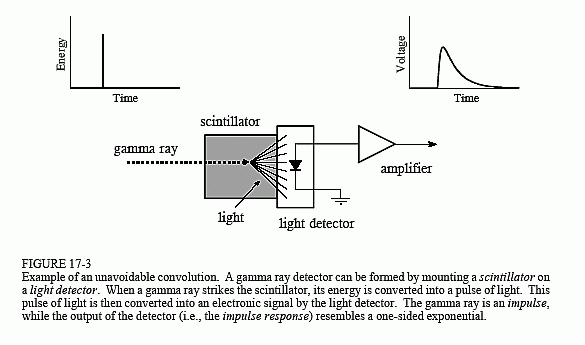
se convierte entonces en una señal electrónica mediante un detector de luz, como un fotodiodo o un tubo fotomultiplicador. Cada pulso producido por el detector se asemeja a una exponencial de un solo lado, con un cierto redondeo de las esquinas. Esta forma viene determinada por las características del centelleador utilizado. Cuando un rayo gamma deposita su energía en el centelleador, los átomos cercanos se excitan a un nivel de energía más alto. Estos átomos se desexcitan aleatoriamente, produciendo cada uno de ellos un único fotón de luz visible. El resultado neto es un pulso de luz cuya amplitud decae en unos cientos de nanosegundos (para el yoduro de sodio). Dado que la llegada de cada rayo gamma es un impulso, el pulso de salida del detector (es decir, el exponencial unilateral) es la respuesta al impulso del sistema.

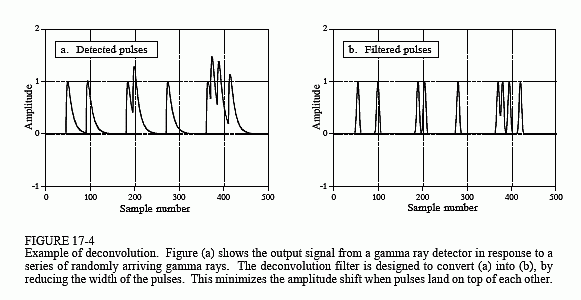
La figura 17-4a muestra los pulsos generados por el detector en respuesta a los rayos gamma que llegan al azar. La información que queremos extraer de esta señal de salida es la amplitud de cada pulso, que es proporcional a la energía del rayo gamma que lo generó. Se trata de una información útil porque la energía puede decir cosas interesantes sobre dónde ha estado el rayo gamma. Por ejemplo, puede proporcionar información médica sobre un paciente, decir la edad de una galaxia lejana, detectar una bomba en el equipaje de un avión, etc.

Todo estaría bien si sólo se detectara un rayo gamma ocasional, pero esto no suele ser así. Como se muestra en (a), dos o más pulsos pueden superponerse, desplazando la amplitud medida. Una respuesta a este problema es deconvolver la señal de salida del detector, haciendo que los pulsos sean más estrechos para que se produzca un menor apilamiento. Lo ideal sería que cada pulso se pareciera al impulso original. Como se puede sospechar, esto no es posible y debemos conformarnos con un pulso de longitud finita, pero significativamente más corto que el pulso detectado. Este objetivo se ilustra en la Fig. 17-4b.

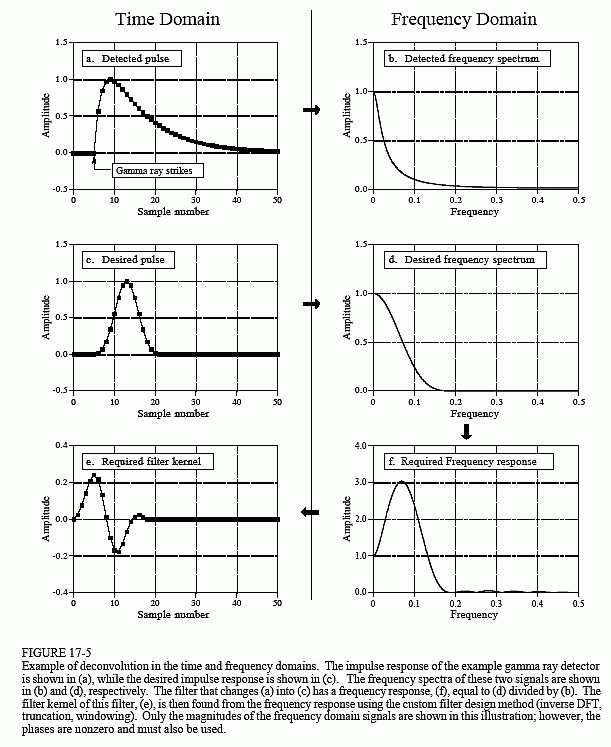
Aunque la señal del detector tiene su información codificada en el dominio del tiempo, gran parte de nuestro análisis debe hacerse en el dominio de la frecuencia, donde el problema es más fácil de entender. La figura 17-5a es la señal producida por el detector (algo que conocemos). La figura (c) es la señal que deseamos tener (también algo que conocemos). Este pulso deseado fue seleccionado arbitrariamente para tener la misma forma que una ventana Blackman, con una longitud de aproximadamente un tercio de la del pulso original. Nuestro objetivo es encontrar un núcleo de filtro, (e), que cuando se convierta con la señal en (a), produce la señal en (c). En forma de ecuación: si a * e = c, y dados a y c, encontrarde.

Si estas señales se combinaran por adición o multiplicación en lugar de porconvolución, la solución sería fácil: la sustracción se utiliza para «des-añadir» y la división se utiliza para «des-multiplicar». La convolución es diferente; no hay una simple operacióninversa que pueda llamarse «deconvolución». La convolución es demasiado complicada como para deshacerla manipulando directamente las señales del dominio del tiempo.

Afortunadamente, este problema es más sencillo en el dominio de la frecuencia. Recuerde, la convolución en un dominio se corresponde con la multiplicación en el otro dominio. Nuevamente refiriéndonos a las señales de la Fig. 17-5: si b × f = d, y dados b y d, encuentre f. Este es un problema fácil de resolver: la respuesta en frecuencia del filtro, (f), es el espectro de frecuencia del pulso deseado, (d), dividido por el espectro de frecuencia del pulso detectado, (b). Como el pulso detectado es asimétrico, tendrá una fase distinta de cero. Esto significa que se debe utilizar una división compleja (es decir, una magnitud & fase dividida por otra magnitud & fase). En caso de que lo haya olvidado, el capítulo 9 define cómo realizar una división compleja de un espectro por otro. El núcleo de filtro requerido, (e), se encuentra entonces a partir de la respuesta de frecuencia por el método de filtro personalizado (IDFT, desplazamiento, truncamiento, &multiplicación por una ventana).

Hay límites a la mejora que puede proporcionar la deconvolución. En otras palabras, si te vuelves codicioso, las cosas se desmoronan. Ser codicioso en este ejemplo significa tratar de hacer el pulso deseado excesivamente estrecho. Veamos lo que ocurre. Si el pulso deseado se hace más estrecho, su espectro de frecuencia debe contener más componentes de alta frecuencia. Como estos componentes de alta frecuencia están en una amplitud muy baja en el pulso detectado, el filtro debe tener una ganancia muy alta en estas frecuencias. Por ejemplo, (f) muestra que algunas frecuencias deben multiplicarse por un factor de tres para lograr el pulso deseado en (c). Si el pulso deseado se hace más estrecho, la ganancia del filtro de deconvolución será aún mayor en las frecuencias altas.

El problema es que los pequeños errores no perdonan en esta situación. Por ejemplo, si alguna frecuencia se amplifica en 30, cuando sólo se requiere 28, la señal deconvolucionada probablemente será un desastre. Cuando la deconvolución se lleva a mayores niveles de rendimiento, las características de la convolución no deseada deben entenderse con mayor exactitud y precisión. Siempre hay incógnitas en las aplicaciones del mundo real, causadas por villanos como: el ruido electrónico, la deriva de la temperatura, la variación entre dispositivos, etc. Estas incógnitas limitan el funcionamiento de la deconvolución.

Incluso si la convolución no deseada se entiende perfectamente, hay un factor que limita el rendimiento de la deconvolución: el ruido. Por ejemplo, la mayoría de las convoluciones no deseadas toman la forma de un filtro de paso bajo, reduciendo la amplitud de los componentes de alta frecuencia en la señal. La deconvolución corrige esto amplificando estas frecuencias. Sin embargo, si la amplitud de estos componentes cae por debajo del ruido inherente al sistema, la información contenida en estas frecuencias se pierde. Ningún tratamiento de la señal puede recuperarla. Se pierde para siempre. Adiós. Adiós. ¡Sayonara! Tratar de recuperar estos datos sólo amplificará el ruido. Como caso extremo, la amplitud de algunas frecuencias puede reducirse completamente a cero. Esto no sólo borra la información, sino que intentará que el filtro de deconvolución tenga una ganancia infinita en esas frecuencias. La solución: diseñar un filtro de deconvolución menos agresivo y/o poner límites a la ganancia permitida en cualquiera de las frecuencias.

¿Hasta dónde se puede llegar? ¿Cuánta ganancia es demasiado? Esto depende totalmente del problema que está atacando. Si la señal se comporta bien y tiene poco ruido, es probable que se pueda hacer una mejora significativa (piense en un factor de 5-10). Si la señal cambia con el tiempo, no se entiende muy bien o tiene mucho ruido, no será tan fácil (piense en un factor de 1-2). El éxito de la deconvolución implica una gran cantidad de pruebas. Si funciona a cierto nivel, intente ir más lejos; sabrá cuando se desmorona. Ninguna cantidad de trabajo teórico le permitirá evitar este proceso iterativo.

La deconvolución también puede aplicarse a las señales codificadas en el dominio de la frecuencia. Un ejemplo clásico es la restauración de antiguas grabaciones del famoso cantante de ópera Enrico Caruso (1873-1921). Estas grabaciones se hicieron con un equipo muy primitivo para los estándares modernos. El problema más importante son las resonancias de la larga trompa de grabación utilizada para recoger el sonido. Cada vez que el cantante toca una de estas frecuencias de resonancia, el ruido de la grabación aumenta bruscamente. La deconvolución digital ha mejorado la calidad subjetiva de estas grabaciones al

reducir los puntos fuertes de la música. Sólo describiremos el método general; para una descripción detallada, véase el artículo original: T. Stockham, T. Cannon y R. Ingebretsen, «Blind Deconvolution Through Digital Signal Processing»,Proc. IEEE, vol. 63, abr. 1975, pp. 678-692.

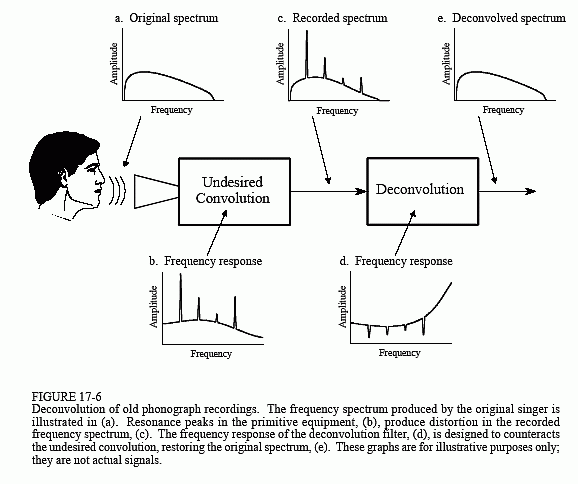
La figura 17-6 muestra el enfoque general. El espectro de frecuencia de la señal de audio original se ilustra en (a). La figura (b) muestra la respuesta en frecuencia del equipo de grabación, una curva relativamente suave excepto por varios picos de resonancia agudos. El espectro de la señal grabada, mostrado en (c), es igual al espectro verdadero, (a), multiplicado por la respuesta en frecuencia desigual, (b). El objetivo de la deconvolución es contrarrestar la convolución no deseada. En otras palabras, la respuesta en frecuencia del filtro de deconvolución,(d), debe ser la inversa de (b). Es decir, cada pico en (b) se cancela con la correspondiente caída en (d). Si este filtro estuviera perfectamente diseñado, la señal resultante tendría un espectro, (e), idéntico al del original.

Aquí está el truco: el equipo de grabación original ha sido desechado hace tiempo, y su respuesta en frecuencia, (b), es un misterio. En otras palabras, se trata de un problema de deconvolución a ciegas; dado sólo (c), ¿cómo podemos determinar (d)?

Los problemas de deconvolución a ciegas suelen atacarse haciendo una estimación o suposición sobre los parámetros desconocidos. Para tratar este ejemplo, se supone que el espectro medio de la música original coincide con el espectro medio de la misma música interpretada por un cantante actual utilizando un equipo moderno. El espectro medio se encuentra mediante las técnicas del capítulo 9: dividir la señal en un gran número de segmentos, tomar la DFT de cada segmento, convertirla en forma polar y luego promediar las magnitudes juntas. En el caso más sencillo, la respuesta en frecuencia desconocida se toma como el espectro medio de la grabación antigua, dividido por el espectro medio de la grabación moderna. (El método utilizado por Stockham et al. se basa en una técnica más sofisticada denominada procesamiento homomórfico, que proporciona una mejor estimación de las características del sistema de grabación).