por Marco Taboga, PhD
La función indicadora de un suceso es una variable aleatoria que toma valor 1 cuando el suceso ocurre y valor 0 cuando el suceso no ocurre. Las funciones indicadoras se utilizan a menudo en la teoría de la probabilidad para simplificar la notación y demostrar teoremas.
Definición
La siguiente es una definición formal.
Definición Sea 
un espacio muestral y un suceso. La función indicadora (o variable aleatoria indicadora) del suceso , denotada por , es una variable aleatoria definida como sigue: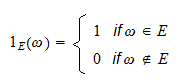
Aunque el indicador de un evento suele denotarse por , a veces también se denota por donde es la letra griega Chi.
Ejemplo Lanzamos un dado y uno de los seis números del 1 al 6 puede aparecer boca arriba. El espacio muestral esDefine el suceso descrito por la frase «Aparece un número par boca arriba». Una variable aleatoria que toma valor 1 cuando aparece un número par boca arriba y valor 0 en caso contrario es un indicador del suceso . La definición casuística de este indicador es
A partir de la definición anterior, puede verse fácilmente que es una variable aleatoria discreta con soporte y función de masa de probabilidad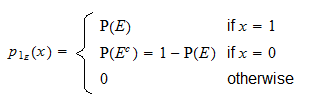
Propiedades
Las funciones indicadoras gozan de las siguientes propiedades.
Potencias
La ésima potencia de es igual a :porque puede ser o y
Valor esperado
El valor esperado de es igual a :
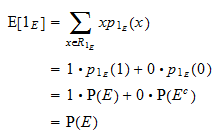
Varianza
La varianza de es igual a . Gracias a la fórmula habitual de la varianza y a la propiedad de las potencias anterior, obtenemos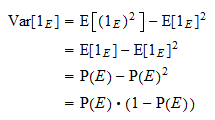
Intersecciones
Si y son dos sucesos, entonces:
-
si
, entonces y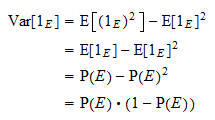
-
si
, entoncesy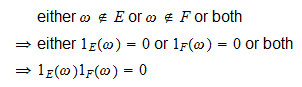
Indicadores de sucesos de probabilidad cero
Sea un suceso de probabilidad cero y una variable aleatoria integrable. Entonces,Si bien una demostración rigurosa de este hecho está fuera del alcance de esta exposición introductoria, esta propiedad debería ser intuitiva. La variable aleatoria es igual a cero para todos los puntos de la muestra excepto posiblemente para los puntos . El valor esperado es una media ponderada de los valores que puede tomar , donde cada valor se pondera por su respectiva probabilidad. Los valores no nulos que puede tomar están ponderados por probabilidades nulas, por lo que debe ser cero.
Ejercicios resueltos
A continuación puedes encontrar algunos ejercicios con soluciones explicadas.
Ejercicio 1
Considere una variable aleatoria y otra variable aleatoria definida como función de .
Exprese utilizando las funciones indicadoras de los sucesos y .
Denote por el indicador del suceso y denote por el indicador del suceso . Podemos escribir como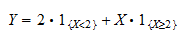
Ejercicio 2
Sea una variable aleatoria positiva, es decir, una variable aleatoria que sólo puede tomar valores positivos. Sea una constante. Demuestre que donde es el indicador del suceso .
Note primero que la suma de los indicadores y es siempre igual a :Como consecuencia, podemos escribir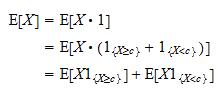
Ahora, note que es una variable aleatoria positiva y que el valor esperado de una variable aleatoria positiva es positivo:Por tanto,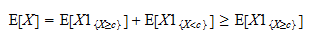
Ejercicio 3
Sea un suceso y denotemos su función indicadora por . Sea el complemento de y denote su función indicadora por . ¿Se puede expresar como función de ?
La suma de los dos indicadores es siempre igual a :Por tanto,
Cómo citar
Por favor, cite como:
Taboga, Marco (2017). «Funciones indicadoras», Conferencias sobre teoría de la probabilidad y estadística matemática, Tercera edición. Kindle Direct Publishing. Apéndice en línea. https://www.statlect.com/fundamentals-of-probability/indicator-functions.