Qué es la forma pendiente intercepción

La forma pendiente intercepción es una de las tres formas que podemos utilizar para expresar una recta. Las otras formas se llaman forma de pendiente de punto y forma estándar, pero en esta sección utilizaremos principalmente la forma de intercepción de pendiente. Usando la forma de intercepción de pendiente, expresamos la ecuación de una recta como:

y=mx+by = mx + by=mx+b

Puede que sepas que xxx e yyy son las coordenadas de un punto en una gráfica, pero ¿qué son mmm y bbb?

¿Qué es b en y=mx+b?

La letra b es un número que representa cuando la recta toca el eje y. También nos referimos a esto como la «intersección y». Por ejemplo, vamos a dibujar una recta en el plano de coordenadas.

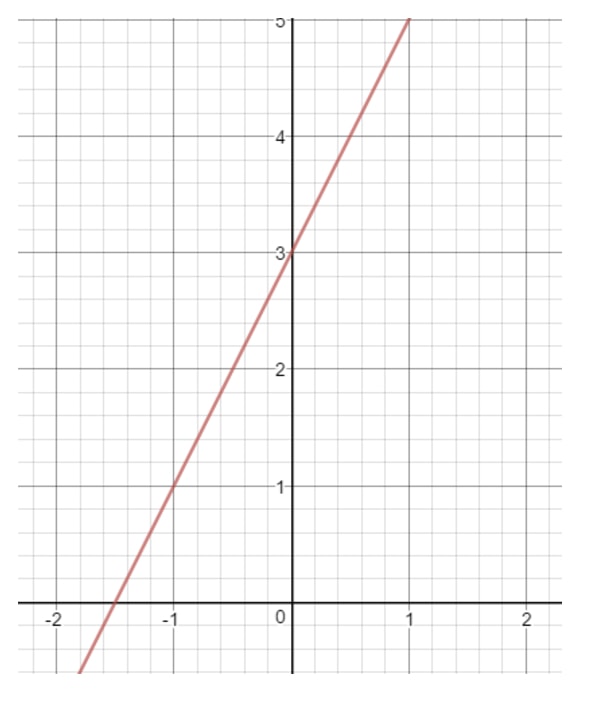
Si te fijas bien en el eje y, la recta toca el eje y en un lugar concreto. ¿Dónde está ese lugar? Sería el número 3 porque ahí es donde el eje y y la recta se cruzan. Esto significa que podemos concluir que b = 3.

¿Qué es m en forma de intercepción de pendientes?

La letra m es un número que representa la pendiente de la recta. Algunos se refieren a la pendiente como subida sobre bajada. Recordemos que si tenemos dos puntos, entonces somos capaces de encontrar la pendiente de los dos puntos utilizando la fórmula de la pendiente

m=riserun=y2-y1x2-x1m = \frac{subida}{corrida} = \frac{y_{2} – y_{1}{x_{2}}} – x_{1}}m=runrise=x2-x1y2-y1

La misma idea funciona aquí. ¡Si tomamos dos puntos cualesquiera en una línea recta, entonces podemos encontrar la pendiente de la línea usando la fórmula anterior! Por ejemplo, usemos esta recta.

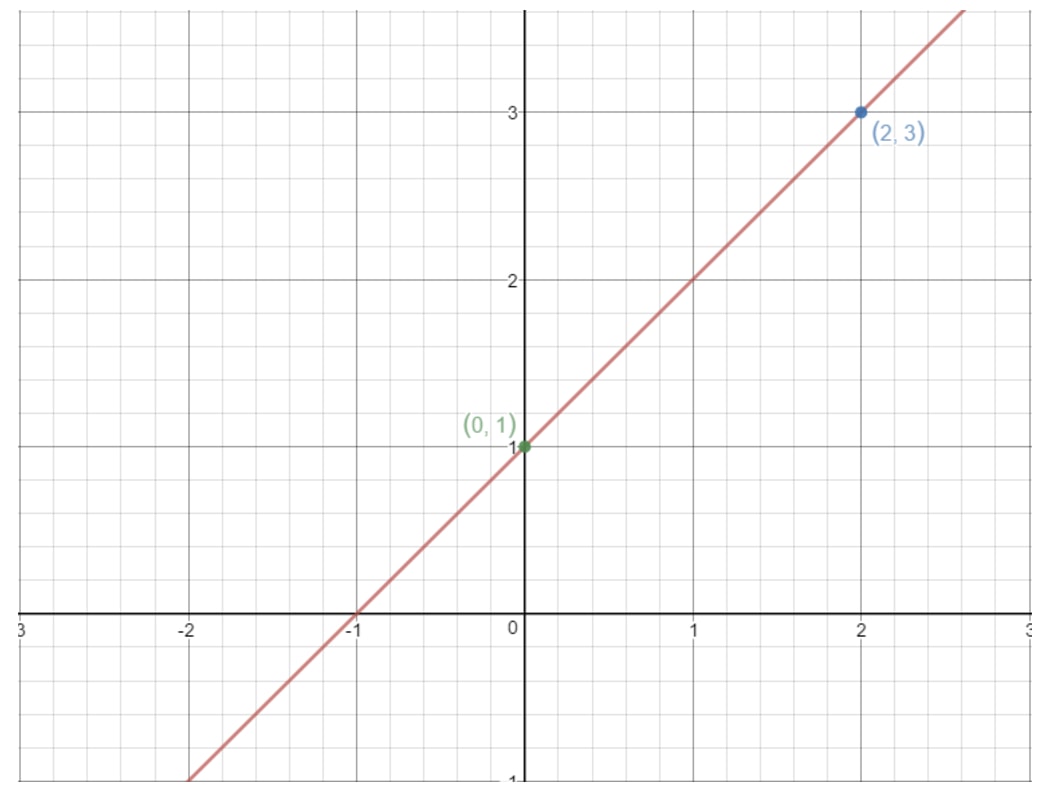
Nota que los puntos (2, 3) y (0, 1) están en esta gráfica. Entonces, ¿por qué no usamos estos dos puntos para encontrar la pendiente de la recta? Utilizando la fórmula, obtendríamos:

m=y2-y1x2-x1=1-30-2m = \frac{y_{2} – y_{1}{x_{2} – x_{1}} = \frac{1 – 3}{0 – 2}m=x2-x1y2-y1=0-21-3=-2-2= \frac{-2}{-2}=-2-2=1=1

Eso significa que la pendiente de esta recta es 111¡

Lo especial de las pendientes es que podemos usar dos puntos cualesquiera de la recta para encontrarla. Así que si tomaras dos puntos diferentes de esta recta, seguirías obteniendo que la pendiente es 111.

¿Cómo escribir una ecuación en forma de intercepción de pendiente?

Puedes saber cómo es la forma de intercepción de pendiente, pero la mitad de las veces te darán ecuaciones que no están en esa forma. Así que tu trabajo es convertirla en la forma pendiente-intercepto. ¿Cómo lo hacemos? El objetivo es aislar siempre el término yyy. Por ejemplo, digamos que te dan la ecuación

6x+4+2y=06x + 4 + 2y = 06x+4+2y=0

Para aislar yyy, movemos el 6x+46x + 46x+4 al lado derecho de la ecuación

2y=-6x-42y = -6x – 42y=-6x-4

Ahora el 222 está en el camino de yyy, así que vamos a deshacernos de él dividiendo ambos lados de la ecuación por 222.

2y2=-6x-42\frac{2y}{2} = \frac{6x – 4}{2}22y=2-6x-4y=-6×2-42y = -\frac{6x}{2} – \frac{4}{2}y=-26x-24y=-3x-2y = -3x – 2y=-3x-2

Dado que yyy está aislado, se puede ver que está en forma de intercepción de pendiente y=mx+by = mx + by=mx+b donde m=-3m = -3m=-3, y b=-2b = -2b=-2.

Ahora que conocemos muy bien el intercepto de y y la pendiente, ¡por qué no miramos preguntas específicas sobre cómo encontrarlos!

¿Cómo encontrar la intercepción de y?

Pregunta 1: Usando la ecuación lineal y=12x+5y = \frac{1}{2} x + 5y=21x+5, encuentra la intercepción de y.

Nota aquí que la ecuación ya está en la forma de intercepción de la pendiente y=mx+by = mx + by=mx+b. Sólo tenemos que averiguar cuál es bbb. Podemos ver que b=5b = 5b=5, por lo que la intercepción de y es 555.

Hagamos una pregunta un poco más difícil.

Pregunta 2: Determina la intercepción de y de 2x-4y=82x – 4y = 82x-4y=8

Ahora esta ecuación lineal no está en forma de intercepción de pendiente, por lo que primero tenemos que cambiarla a esa forma. Nuestro objetivo es aislar yyy en esta ecuación.

Veamos que si movemos el 2x2x2x al lado derecho de la ecuación, tendremos:

-4y=8-2x-4y = 8 – 2x-4y=8-2x

Ahora dividiendo ambos lados por -4-4-4, obtendremos:

-4y-4=8-2x-4\frac{-4y}{-4} = \frac{8 – 2x}{-4}-4y=-48-2xy=8-4-2x-4y = \frac{8}{-4} – \frac{2x}{-4}y=-48–42xy=-2+12xy = -2 + \frac{1}{2}xy=-2+21x

Ahora cambiando las posiciones de los dos términos nos da:

y=12x-2y = \frac{1}{2}x – 2y=21x-2

Pregunta 3: Determina el intercepto y de 4y-8=04y – 8 = 04y-8=0.

Esto puede parecer un poco raro porque no hay término xxx, pero nuestro objetivo sigue siendo el mismo. Vamos a aislar yyy.

Moviendo el -8-8-8 al lado derecho de la ecuación nos da:

4y=84y = 84y=8

Dividiendo ambos lados de la ecuación por 444 nos da

4y4=84\frac{4y}{4} = \frac{8}{4}44y=48y=2y = 2y=2

Ahora esto puede no parecerlo, pero la ecuación está en forma de intercepción de la pendiente. Es que m=0m = 0m=0, por lo que todo el término mxmxmx ha desaparecido. Sólo tienes que reescribir la ecuación como

y=0m+2y = 0m + 2y=0m+2

De la observación se desprende que b=2b = 2b=2, por lo que el intercepto y es 222. Hagamos una pregunta más.

Pregunta 4: Determina (si es posible) la intercepción y de 5x-15=05x – 15 = 05x-15=0.

Esta es interesante porque la ecuación no tiene término yyy. Entonces, ¿cómo vamos a ponerla en forma de intercepción de la pendiente? Bueno, lo único que podemos hacer ahora es aislar para xxx, así que vamos a intentar eso por ahora.

Moviendo el 151515 al lado derecho de la ecuación tenemos:

5x=155x = 155x=15

Dividiendo ambos lados de la ecuación da:

5×5=155\frac{5x}{5} = \frac{15}{5}55x=515x=3x = 3x=3

Ahora vamos a dibujar esto en una gráfica. Observa que en esta ecuación, xxx está obligado a ser 333 y no puede ser otra cosa. Sin embargo, no dice nada sobre yyy, así que yyy puede ser lo que quiera. Si escribiéramos una tabla de valores, obtendríamos:

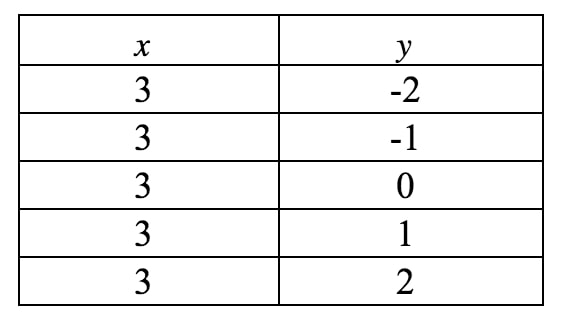
Si trazamos estos puntos en un plano de coordenadas y dibujamos la recta, tenemos:

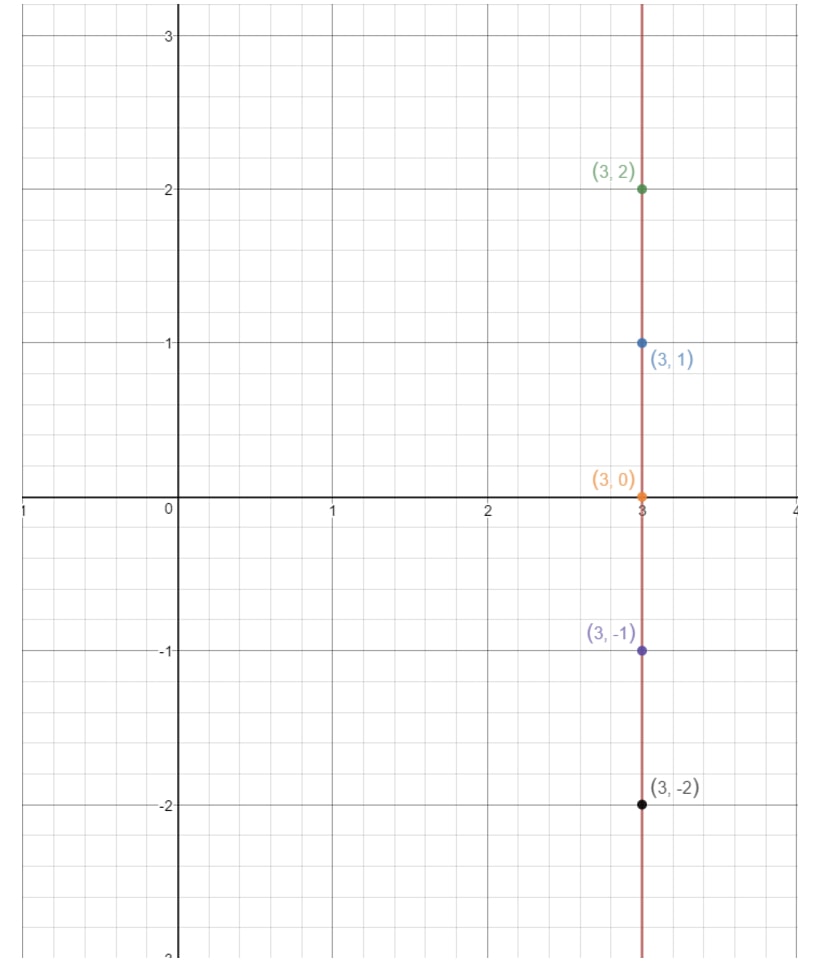
Nota cómo la recta nunca toca el eje y. Esto significa que la ecuación no tiene una intercepción en y. Ahora que hemos cubierto todos los casos de encontrar el intercepto y, vamos a ver las preguntas que nos piden encontrar la pendiente!

¿Cómo encontrar la pendiente de una ecuación?

Pregunta 5: Halla la pendiente de y=32x+1y = \frac{3}{2}x + 1y=23x+1

Pregunta 6: Determina la pendiente de la ecuación lineal 6x-6y=06x – 6y = 06x-6y=0

Como puedes ver, la ecuación no está en forma de intercepción de la pendiente, así que primero tenemos que convertirla a esa forma. Nuestro objetivo es aislar yyy.

Moviendo 6x6x6x al lado derecho de la ecuación da:

-6y=-6x-6y = -6x-6y=-6x

Dividiendo ambos lados por -6-6-6 da:

-6y-6=-6x-6\frac{-6y}{-6} = \frac{-6x}{-6}-6-6y=-6xy=xy = xy=x

Nota que esto es en realidad en forma de intercepción de pendiente y=mx+by = mx + by=mx+b. Es que el intercepto y bbb en este caso es 000, y xxx es lo mismo que 1x1x1x. Así que podemos reescribir la ecuación a:

y=1x+0y = 1x + 0y=1x+0

Ahora observando, vemos que m=1m = 1m=1. Como mmm es la pendiente, entonces la pendiente debe ser 111. Hagamos una un poco más difícil

Pregunta 7: Determina la pendiente de 2y-4=02y – 4 = 02y-4=0

De nuevo, esto es un poco raro porque no tenemos ningún término xxx. Sin embargo, nuestro objetivo de aislar yyy sigue siendo el mismo.

Moviendo -4-4-4 al lado derecho de la ecuación tenemos:

2y=42y = 42y=4

Dividiendo ambos lados de la ecuación por 222 da:

2y2=42\frac{2y}{2} = \frac{4}{2}22y=24y=2y = 2y=2

Vea aquí que ahora está en forma de intercepción de pendiente, excepto que el término mxmxmx está oculto porque m=0m = 0m=0. Así que podemos reescribir nuestra ecuación como:

y=0x+2y = 0x + 2y=0x+2

Como m=0m = 0m=0, entonces tenemos una pendiente cero. Si te preguntas cómo es una recta con pendiente 000, aquí tienes una gráfica para que la veas.

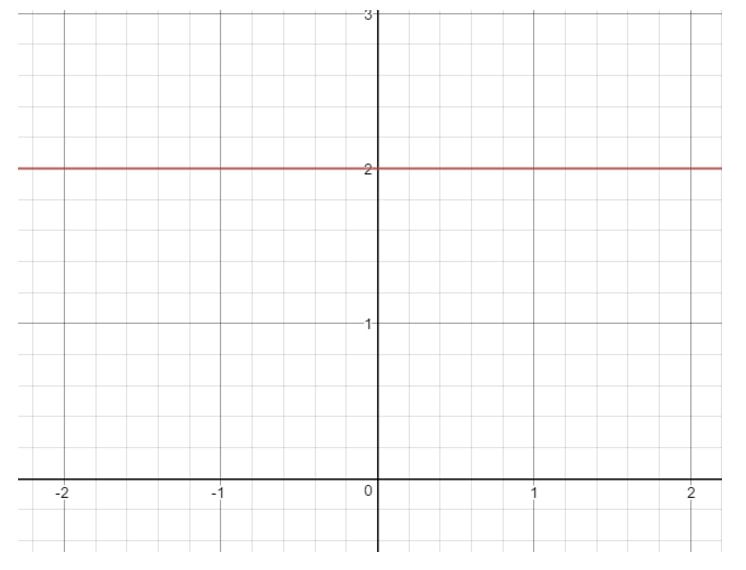
Pregunta 8: Halla (si es posible) la pendiente de la ecuación lineal 16-4x=016 – 4x = 016-4x=0

En este caso, no se puede aislar yyy porque no hay término yyy. Así que lo único que podemos hacer es aislar xxx.

Moviendo 161616 al lado derecho de la ecuación se obtiene:

-4x=-16-4x = -16-4x=-16

Dividiendo ambos lados por -4-4-4, obtenemos:

-4x-4=-16-4\frac{-4x}{-4} = \frac{-16}{-4}-4-4x=-4-16x=4x = 4x=4

Esto todavía no está en forma de intercepción de la pendiente, por lo que nuestra única esperanza de obtener la pendiente es dibujar una gráfica de esta línea. De nuevo, vemos que xxx siempre está obligado a ser 444, pero yyy puede ser lo que quiera porque no hay ningún término yyy. Si escribiéramos una tabla de valores, obtenemos:

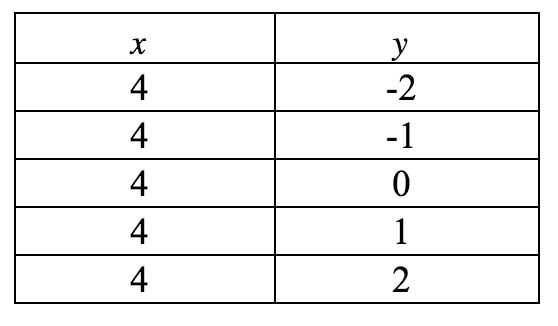
Si trazamos estos puntos en un plano de coordenadas y dibujamos la recta, tenemos:

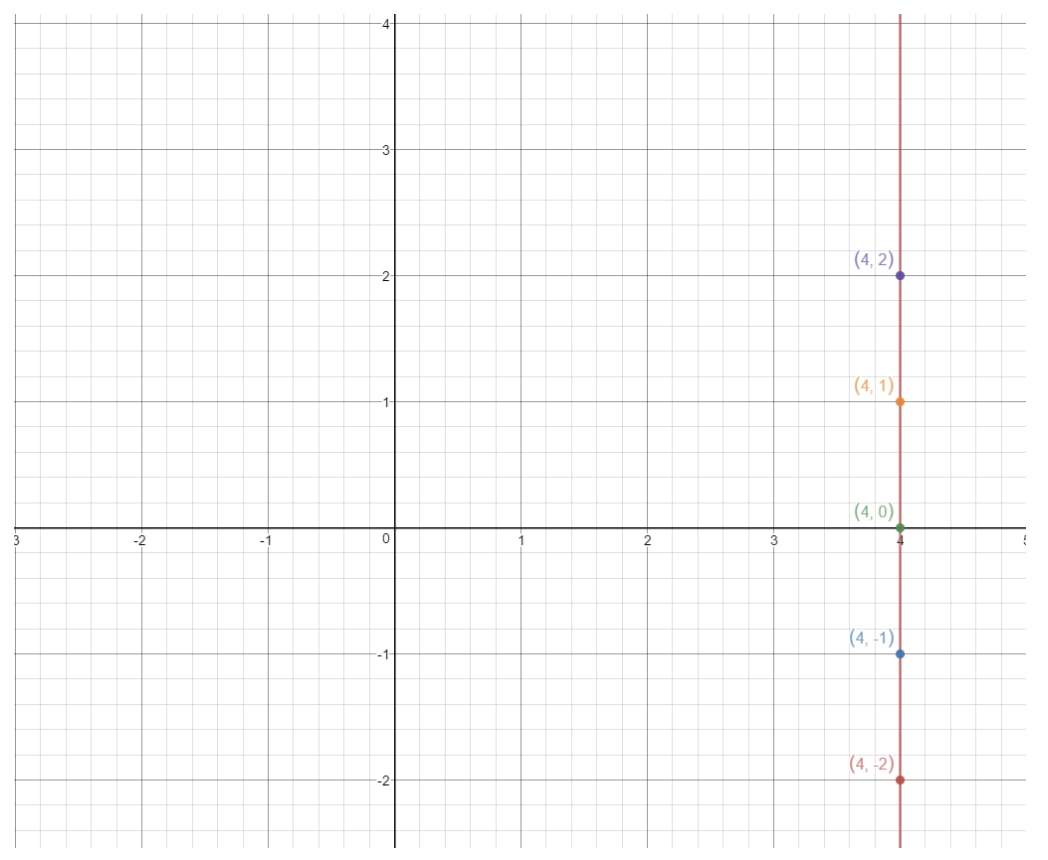
Esto es una recta vertical. Entonces, ¿cuál es la pendiente de una recta vertical? Vamos a intentar averiguarlo encontrando la subida y el recorrido. Mira cómo esta línea siempre está subiendo infinitamente, pero no hay ninguna carrera en absoluto. Eso significa que el recorrido es 000. Así que si calculamos la pendiente, entonces obtendremos:

m=riserun=rise0=undefinedm = \frac{rise}{run} = \frac{rise}{0} = undefinedm=runrise=0rise=undefined

No podemos dividir por 000, así que en realidad tenemos una pendiente indefinida.

¿Qué es una pendiente indefinida?

Una pendiente indefinida es una pendiente que va hacia arriba en la gráfica. Como se ve en la gráfica anterior, la pendiente sube infinitamente y no tiene recorrido. Como resultado, obtenemos una pendiente indefinida porque no podemos dividir por 000.

En general, siempre obtenemos una pendiente indefinida cuando obtenemos una línea vertical recta!

Veamos otras preguntas únicas!

Hallar la ecuación a partir de un punto

Pregunta 9: Un punto (2, 6) pasa por una ecuación de y=-5x+by = -5x + by=-5x+b. Halla «bbb».

6=-5(2)+b6 = -5(2) + b6=-5(2)+b

Aislando y resolviendo para bbb se obtiene:

6=-10+b6 = -10 + b6=-10+bb=16b = 16b=16

Recuerda que bbb también se conoce como la intersección en y, ¡así que la intercepción en y también es 161616!

Hallar la pendiente a partir de dos puntos

Pregunta 10: Dados dos puntos (6, 1) y (-10, 9), hallar la pendiente de la recta.

Recordemos que para hallar la pendiente de la recta, utilizamos la ecuación de la pendiente

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=x2-x1y2-y1

Por lo tanto, utilizando esta fórmula nos da:

m=9-1-10-6=8-16m = \frac{9 – 1}{-10 – 6} = \frac{8}{-16}m=-10-69-1=-168=1-2= \frac{1}{-2}=-21

¿Y si en cambio se supone que debemos encontrar la ecuación completa de una recta?

Ecuación de una recta dados dos puntos

Pregunta 11: Dados dos puntos (-6, 1) y (2, 6), encontrar la ecuación de la forma de intercepción de la pendiente.

Básicamente estamos tratando de encontrar la ecuación en la forma de y=mx+by = mx + by=mx+b. Para ello, tenemos que buscar mmm y bbb.

Recordemos que para encontrar mmm, utilizamos la ecuación de la pendiente

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}{x_{2} – x_{1}}m=x2-x1y2-y1

Por lo tanto, utilizando esta fórmula nos da:

m=6-12-(-6)=58m = \frac{6 – 1}{2 – (-6)} = \frac{5}{8}m=2-(-6)6-1=8558\frac{5}{8}85

Así que ahora tenemos la ecuación

y=58x+by = \frac{5}{8}x + by=85x+b

Ahora tenemos que buscar bbb. Para resolver bbb, elegimos cualquiera de los puntos dados y lo introducimos en la ecuación. Podemos hacerlo porque ambos puntos se encuentran en la recta, y cualquier punto de la recta satisfaría la ecuación. Utilicemos el punto (2, 6). Observa que:

6=58(2)+b6 = \frac{5}{8}(2) + b6=85(2)+b

Aislando bbb se obtiene:

6=108+b6 = \frac{10}{8} + b6=810+bb=6-108b = 6 – \frac{10}{8}b=6-810b=488-108b = \frac{48}{8} – \frac{10}{8}b=848-810b=388b = \frac{38}{8}b=838

Poniendo esto en forma decimal, obtenemos que b=4,75b = 4,75b=4,75. Por lo tanto, nuestra ecuación en forma de intercepción de pendiente es:

y=58x+4,75y = \frac{5}{8}x + 4,75y=85x+4,75

Lo último que hay que cubrir en esta sección es hallar el dominio y el rango de una recta.

¿Cómo hallar el dominio y el rango?

Para hallar el dominio de una recta, básicamente nos hacemos esta pregunta: ¿qué puede ser xxx? Si xxx puede ser esos valores, entonces los añadimos al dominio.

Lo mismo ocurre con el rango. ¿Qué puede ser yyy? Si yyy pueden ser esos valores, entonces los añadimos en el rango. Hagamos un ejemplo.

Pregunta 12: Encuentra el dominio y el rango de la ecuación y=2x+1y = 2x + 1y=2x+1.

Nota que si dibujamos la gráfica de esta recta, entonces obtendremos:

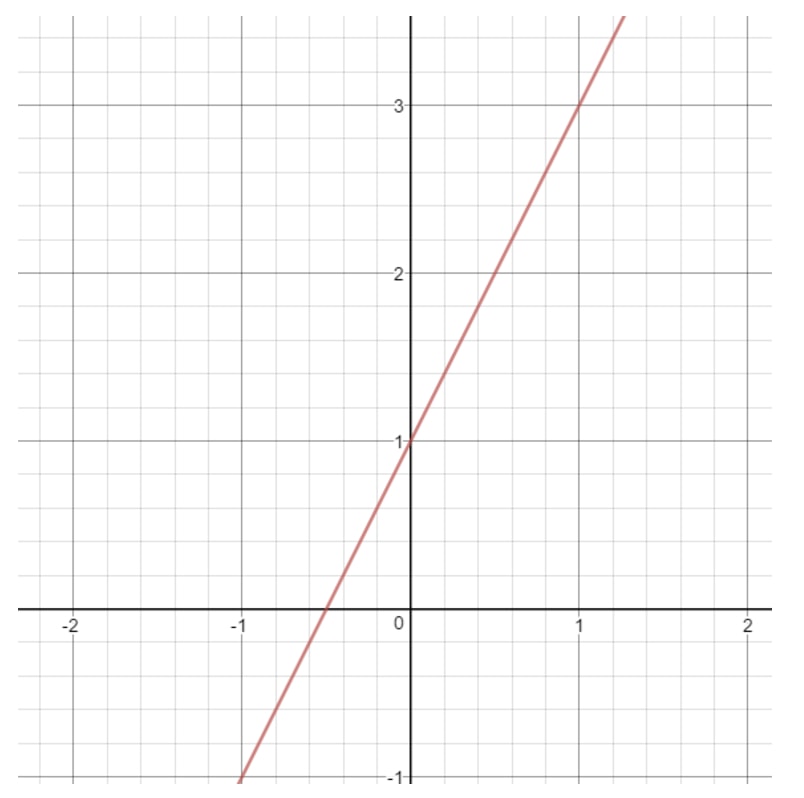
¿Qué puede ser xxx en esta recta? Observa que xxx puede ser cualquier cosa porque con cualquier valor de xxx podemos obtener un punto que esté en la recta. Lo mismo ocurre con y. Siempre podemos elegir un valor yyy que nos dé un punto en una recta. Así que decimos que

Dominio: {x∈\in∈R}Rango: {y∈\in∈R}

donde R significa «todos los números reales». Hagamos una más difícil.

Pregunta 13: Encuentra el dominio y el rango de la ecuación y=-2y = -2y=-2.

Ahora bien, si dibujamos esta recta en una gráfica, obtendremos:

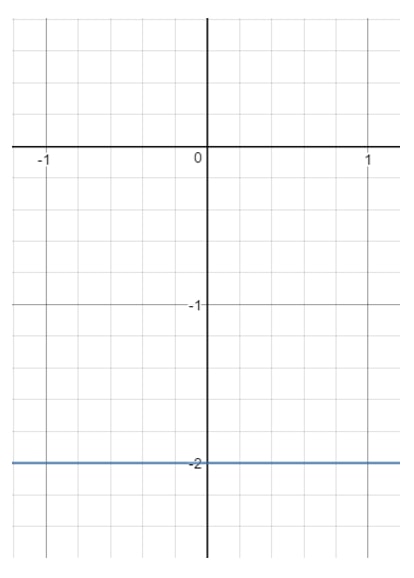
Nota que xxx puede ser cualquier cosa porque con cualquier valor de xxx, podemos obtener un punto que esté en la recta siempre que y=-2y = -2y=-2. Sin embargo, fíjate en yyy. Ves que yyy está forzado a -2-2-2 y no puede ser otra cosa. En el momento en que elijas otro valor de yyy (como 111), ese punto estará fuera de la recta. Así que eso significa:

Dominio: {x ∈\in∈ R}Rango: {y = -2}

Pregunta 14: Halla el dominio y el rango de la ecuación x=1x = 1x=1.

Ahora bien, si dibujamos esta recta en una gráfica, obtendremos:

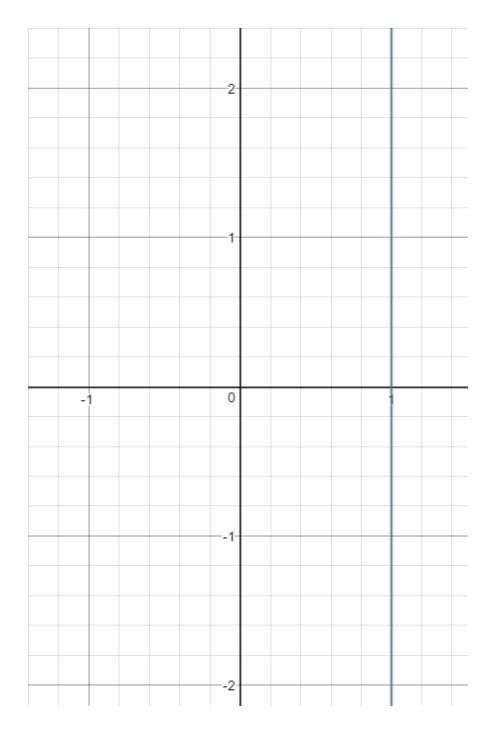
Ves que xxx está obligado a ser 111 y no puede ser otra cosa. En el momento en que elijas otro valor de xxx (como 222), entonces ese punto va a estar fuera de la línea.Sin embargo, mira yyy. Fíjate que yyy puede ser cualquier cosa porque con cualquier valor de yyy, podemos obtener un punto que esté en la recta siempre que x=1x = 1x=1

Entonces eso significa:

Dominio: {x=1}Rango: {y∈\in∈R}

Si has tenido muchos problemas para dibujar las gráficas para obtener el dominio y el rango, te recomiendo que utilices esta calculadora.

https://www.desmos.com/calculator/2rnqgoa6a4

Te enseña a graficar una ecuación lineal. Todo lo que tienes que hacer es escribir los valores de mmm y bbb. Entonces, ¡dibujará automáticamente la línea por ti! Esto también es útil cuando usted está tratando de encontrar la forma de intercepción de la pendiente.