Haluamme tämän koneen tuottavan koko harjoitusaineiston yksin tai tuottavan koko harjoitusaineiston alkuperäisestä aineistosta saadun vihjeen perusteella. Esimerkiksi annettuna vihjeenä bittikarttakuva, joka sisältää ”SCI”, se tuottaisi ”ENCE” itsestään oppimiensa painojen perusteella.

Voidaksemme saada mielikuvamme järjestelmästä, tarkastellaan kuvaa 5.

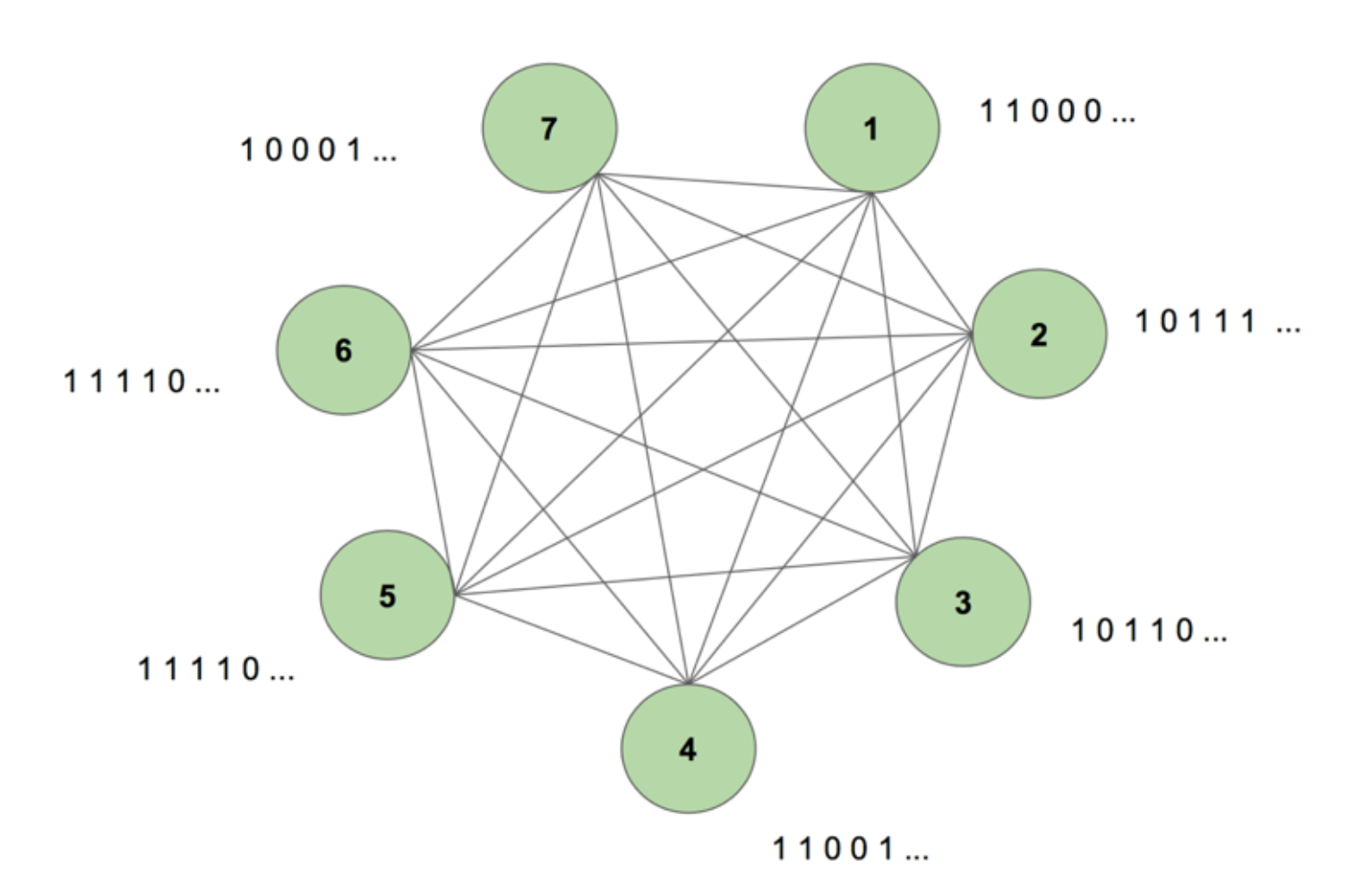
Koneessa on seitsemän solmua. Kohdejonona on 7 x 35 bittikarttakuva, joka esittää sanaa SCIENCE. Yksi harjoitusjakso koostuu siitä, että koneelle näytetään tämä kohdesekvenssi kerran. Kohde pilkotaan 35:een 7 arvoa sisältävään kaistaleeseen ja syötetään koneelle samassa järjestyksessä kuin se esiintyy kohteessa. Kuvassa 5 esitetään, miltä viisi tällaista syöttöliuskaa näyttäisi. Näemme, että bittikarttamme ensimmäinen liuska, joka koostuu kaikista 1:stä, heijastuu solmujen sisääntulojen ensimmäiseen arvoon. Näin syötämme arvot koneeseen harjoittelun aikana.

Kun alustamme koneen ensimmäisen kerran mielivaltaisilla painoilla ja pyydämme sitä luomaan sekvenssin, se luo jotain täysin satunnaista. Kun harjoittelemme konetta 130 000 harjoittelujakson ajan, se pystyy luomaan koko sekvenssin itsestään. Tämä tarkoittaa, että harjoittelun aikana se optimoi painotuksiaan oppiakseen bittien samanaikaisen esiintymisen paitsi yhdessä aikajaksossa, myös koko sekvenssissä.

Magista, eikö olekin? Mutta tämän taikatempun takana on vankka logiikka. Puretaan mysteeri ja katsotaan, miksi tämä ”Boltzmann-kone muistilla” toimii.

Tässä on dynaamisen Boltzmannin koneen (Dynamic Boltzmann Machine (DyBM)) rakenne. Boltzmann-koneessa solmu sisältää tiedon siitä, mitkä solmut aktivoivat sitä tietyllä hetkellä. Tämä tekee sen tietoiseksi tapahtumista, jotka tapahtuvat yhdessä, mutta ei anna sille kykyä tarkastella taaksepäin ja muodostaa assosiaatioita eri aikavaiheiden välillä. DyBM:ssä solmujen väliset yhteydet kuvaavat kuitenkin sitä, miten solmut ovat vuorovaikutuksessa keskenään ajan mittaan, eivät vain tiettynä ajankohtana. DyBM helpottaa tätä lisäämällä solmujen välille johtumisviiveen.

Tässä uudessa arkkitehtuurissa solmulla on tietoa siitä, mitkä muut solmut ovat katalysoineet sen aktivoitumista jollakin aika-askeleella T = t omien toimintojensa kautta menneillä aika-askeleilla T = t – 1, T = t – 2 ja niin edelleen. Tämä ”muisti” lisätään solmuun muistiyksikön muodossa. Tämä yksikkö muuttaa todennäköisyyttä, että solmu aktivoituu millä tahansa hetkellä, riippuen muiden solmujen aiemmista arvoista ja siihen liittyvistä omista painoista.

Asettakaamme, että meillä on kaksi solmua A ja B. Korkealla tasolla laajennamme ajatusta, että ”neuronit, jotka syttyvät yhdessä, kytkeytyvät toisiinsa” yli aikaulottuvuuden. Kuvitellaan esimerkiksi, että A:n aktivoituminen johtaa johdonmukaisesti B:n aktivoitumiseen kahden aika-askeleen jälkeen. Ei-dynaaminen Boltzmann-kone ei pysty vangitsemaan tätä mallia, mutta DyBM:n avulla, koska A:n arvo siirtyy B:hen jonkin viiveen jälkeen, voin vangita mallin, että B = 1 joskus A = 1:n jälkeen. Nyt todennäköisyys sille, että B = 1 aika-askeleella T = t, vaihtelee A:n arvon T = t lisäksi myös A:n arvojen T = t – 1, T = t – 2 ja niin edelleen perusteella, riippuen A:n ja B:n välisen johtumisviiveen määrästä.

Kone tallentaa arvot niin, että viimeisimmät arvot saavat suuremman painoarvon, mikä on järkevää, koska yleensä aikasarjan viimeisimmät osat ovat informatiivisimpia viimeisimmästä trendistä. DyBM tallentaa tämän tiedon kelpoisuusjälkiin. B:n synaptinen kelpoisuusjälki sisältää niiden arvojen painotetun summan, jotka ovat saapuneet B:hen A:sta tietyn johtumisviiveen jälkeen. B:n neuraalinen kelpoisuusjälki (Neural Eligibility Trace of B) sisältää sen aiempien arvojen painotetun summan.

Samankaltaisesti kuin tavalliset rekursiiviset neuroverkot, voimme avata DyBM:ää ajassa. Taiton DyBM on Boltzmann-kone, jolla on ääretön määrä yksiköitä, joista kukin edustaa solmun arvoa tiettynä ajankohtana.

Tämä on siis dynaaminen Boltzmann-kone: arkkitehtuuri, jolla on kyky luoda harjoitusdata uudestaan, ei vain yhtenä ajankohtana, vaan koko kyseisen datan jakson ajan.

DyBM:t ovat kiehtovia, ja seuraava osa ajaa asian perille.

Osa 4: RNN-Gaussian-DyBM:n ja LSTM:n välinen vastakkainasettelu

Kaikki tähän mennessä näkemämme esimerkit ovat käsitelleet binääristä dataa (Bernoulli-jakauma). IBM:n tutkijat menivät askeleen pidemmälle ja loivat DyBM:n, joka pystyi mallintamaan Gaussin jakaumia, ja mahdollistivat meidän kaltaisillemme käyttäjille aikasarjadatan mallintamisen DyBM:n ja sen muunnelmien avulla.

Tarkistaakseni DyBM:n tehokkuuden suoritin joitakin testejä, joissa verrattiin RNN-Gaussian-DyBM:ää (DyBM, jossa on RNN-kerros) ja nykyistä huipputekniikkaa, Long Short Short-Term Memory -neuraalista verkkoa. Tulokset olivat jännittäviä. Voit vapaasti suorittaa nämä testit itse, perustuen täältä löytyvään skriptiin.

Katsotaanpa, miten DyBM vertautuu LSTM:ään aikasarjan käyttötapauksessa.

Käyttötapaus: Ennustetaan seuraavan auringonpilkkuluvun arvo.

Käytetään dataa, joka sisältää Zürichin laboratoriossa lasketun kuukausittaisen auringonpilkkuluvun vuodesta 1749 vuoteen 1983. Data on avointa lähdekoodia ja saatavilla osoitteesta Datamarket – Monthly sunspot number, Zurich, 1749-1983.

Katsotaan ensin, miten LSTM suoriutui.

LSTM

• Arkkitehtuuri: LSTM Dimension = 10.
• Suorituskyky 10 epookin aikana: Mean Test Score LSTM = 0.08877 RMSE
• Per epoch time to learn: 8.689403 sek.

Katsotaan nyt, miten RNN-Gaussian-DyBM suoriutui samasta datasta.

Sitoutukaa, tästä tulee hyvin mielenkiintoinen löytöretki… Valmiina?

RNN-Gaussian-DyBM

• Arkkitehtuuri: RNN Dimension = 10 ja Input Dimension = 1
• Performance over 10 epochs: Mean Test Score LSTM = 0.07848 RMSE
• Per epoch time to learn: 0.90547 sek.

Ei RNN-Gaussian-DyBM toimi tässä tapauksessa ainoastaan 10 kertaa nopeammin, vaan se tarjoaa myös paremman suorituskyvyn.

Kun skaalataan näiden kahden mallin epookkien määrää, näiden kahden mallin harjoittelun aikaero kasvaa jyrkästi. DyBM:n vasteaika on paljon nopeampi, joten train – test – deploy -sykli kutistuu ja malleja voidaan parantaa paljon nopeammin.

Mutta emme ole vielä keskustelleet DyBM:n parhaasta puolesta: Voit nopeuttaa niitä GPU-kiihdytyksellä. DyBM, joka toimii GPU:lla IBM Watson Studio Localissa Power AI IBM Cloud Service -palvelun kanssa, voi tehdä ennusteita yli 2000:lle aikasarjalle, joista jokainen on yli 500 pituinen, alle 10 sekunnissa epookkia kohden. Sitä vastoin CPU:lla toimivalla DyBM:llä samaan tehtävään kuluu hieman yli 30 minuuttia. Vertaa tätä tulosta CPU:lla toimivan LSTM:n suorituskykyyn edellisessä esimerkissä. Kuvittele, millaista laskentatehoa tämä tarjoaa. Katso täältä lisätietoja DyBM:ien kiihdyttämisestä näytönohjaimilla. Kannattaa huomata, että myös LSTM:iä voi kiihdyttää näytönohjaimilla, ja suorituskykyvertailu kiihdytetyn DyBM:n ja kiihdytetyn LSTM:n välillä vaihtelee.

Kun seuraavan kerran haluat ratkaista aikasarja-ongelman, kokeile Dynamic Boltzmann Machinesia. Harkitse aloittamista IBM Research Tokion Dynamic Boltzmann Machinesin GitHub-tietovarastosta, jonka löydät täältä.

Katso alta lisää syvällistä tutkimusta energiapohjaisista malleista, Boltzmannin koneista ja Dynaamisista Boltzmannin koneista:

• A Tutorial on Energy-Based Learning – Yann LeCun, Sumit Chopra, Raia Hadsell, Marc’Aurelio Ranzato, ja Fu Jie Huang
• Boltzmannin koneet – Geoffrey Hinton
• Boltzmannin koneet ja energiapohjaiset mallit – Takayuki Osogami (IBM Research – Tokio)
• Seitsemän neuronia, jotka muistavat aakkosellisten kuvien sekvenssejä piikkien avulla-timing dependent plasticity – Takayuki Osogami and Makoto Otsuka
• Nonlinear Dynamic Boltzmann Machines for Time-Series Prediction – Sakyasingha Dasgupta and Takayuki Osogami (IBM Research – Tokyo)