El modelo Ising es un ejemplo particular de sistema termodinámico, y es el sistema modelo para entender las transiciones de fase. ¿Sabes que muchos biólogos pasan mucho tiempo con míseras moscas de la fruta? Pues bien, los físicos pasan mucho tiempo con el modelo de Ising. Como nos dice el profesor Raghu, es la Drosophila de las transiciones de fase.

Personalmente, no soy el mayor fan de su analogía porque creo que las moscas de la fruta son asquerosas. Esperemos que el modelo de Ising no sea demasiado asqueroso.

Motivación

¿Por qué debemos dedicar tanto tiempo a hablar del modelo de Ising?

• Es sorprendentemente útil para ayudarnos a pensar en todo tipo de comportamientos relacionados con las transiciones de fase. Por ejemplo:

  • el modelo de Ising presenta ruptura de simetría en la fase de baja temperatura (de la que acabamos de hablar)

  • tiene un «punto crítico» especial a una temperatura bien definida (al que aludimos en el diagrama de fase del agua)

  • otras ricas características.

• Es uno de los pocos modelos exactamente solubles en los que podemos calcular cantidades termodinámicas e interpretarlas.

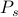  • En general, calcular cantidades termodinámicas es difícil porque hay que sumar muchos términos. Recuerda de nuestra primera clase de termodinámica que puedes pensar en un sistema en equilibrio como un conjunto de muchos estados , cada uno ponderado con su propia probabilidad . En este marco, las cantidades termodinámicas que se observan corresponden a promedios sobre el conjunto. En particular, si quieres encontrar la media del conjunto de algún observable 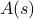, tienes que encontrar la suma 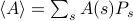, donde la suma corre sobre todos los estados posibles. ¡El problema con esto, como recuerdas, es que el número de estados de un sistema termodinámico escala exponencialmente con el número de partículas! Incluso para un sistema de tamaño moderado, hay demasiados estados para que un ordenador calcule explícitamente la media, por no hablar de un sistema termodinámico en el que 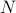es del orden de .

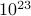  • Así que tenemos que »ser inteligentes» para calcular la función de partición, ¡y deberíamos estar agradecidos por los sistemas exactamente resolubles!

• El modelo de Ising es sencillo, pero puede aplicarse a un número sorprendente de sistemas diferentes.

  • Esta es nuestra primera muestra de universalidad, una característica de los fenómenos críticos en la que la misma teoría se aplica a todo tipo de transiciones de fase diferentes, ya sea en líquidos y gases o imanes o superconductores o lo que sea. A los físicos les encanta este tipo de comportamiento general porque sugiere una especie de orden más profundo en nuestro mundo caótico.

Definición del modelo de Ising

El modelo de Ising es un modelo matemático que no se corresponde con un sistema físico real. Es un enorme entramado (cuadrado) de sitios, donde cada sitio puede estar en uno de dos estados. Etiquetamos cada sitio con un índice , y llamamos a los dos estados y . Para decir que el sitio está en el estado , escribimos .

Ahora bien, esta definición es lamentablemente abstracta y poco física, así que para nosotros, los físicos, es extremadamente útil tener un sistema real en mente, para poder referirnos a algo explícito y construir una intuición física. He aquí algunos sistemas físicos que el modelo Ising podría representar:

• Un imán. Cada sitio representa un «espín» particular en el material (¿un electrón no apareado?), y es si el espín apunta hacia abajo o si el espín apunta hacia arriba. Cada uno de los espines actúa como un mini imán con su propio mini momento magnético; si todos los espines están alineados, entonces toda la red de espines se comporta como un gran imán con un momento magnético neto macroscópico.

• Una aleación; digamos, de latón. Cada uno de los sitios es un átomo en la red; representa un átomo de cobre en ese sitio; representa el zinc.

• Un »gas de red». Cada uno de los sitios es la posible ubicación de una partícula; significa que ese sitio está vacío y significa que ese sitio está ocupado por una partícula.

• ¿Retículas de vórtices bacterianos???

Por ahora, pensaremos en el modelo de Ising como un modelo de imán. Es un modelo muy simplificado y de juguete de un imán, sin duda, pero la analogía del imán puede, no obstante, ayudar a guiar nuestra apreciada intuición física.

Colocando el Hamiltoniano

Una pregunta natural que debemos hacernos sobre este modelo de imán en forma de ratón es qué energía tiene. Para ser más precisos, queremos escribir una función que represente la energía de cada una de las posibles configuraciones (también llamadas microestados) de los espines del imán. Como sabemos, esta función de energía se llama Hamiltoniano.

En el modelo de Ising, el Hamiltoniano incluye dos tipos de interacciones:

• el término de campo externo. Como recordamos de la mecánica cuántica, un campo magnético externo puede dividir las energías de los estados de espín abajo y espín arriba, de manera que uno es más alto en energía y el otro es más bajo.

  • El tamaño de representa lo fuerte que es el campo, por lo que te dice cuánto más alto en energía es un espín que el otro.

  • El signo de te dice si es el espín arriba o el espín abajo el preferido.

  • Dado que cada espín individual siente el campo externo, tenemos que sumar sobre todos los sitios para encontrar la contribución total a la energía.

• El término de interacción entre los espines vecinos – tal vez quieran alinearse entre sí y apuntar en la misma dirección, tal vez quieran antialinearse y apuntar de diferentes maneras. Físicamente, podemos imaginar que esta interacción surge porque cada espín en el imán es su propio mini dipolo magnético que establece su propio campo magnético, y sus vecinos pueden sentir ese campo magnético.

  • El tamaño de indica la fuerza con la que los espines vecinos se acoplan entre sí, es decir, cuánto quieren (anti)alinearse. Físicamente, la fuerza del acoplamiento espín-espín podría depender de la distancia entre ellos en el retículo del maget, por ejemplo.

  • El signo de te dice si los vecinos prefieren alinearse o antialinearse. (El término técnico para esto es ferromagnético o antiferromagnético, respectivamente). Físicamente, que un material sea uno u otro (o ninguno) depende de los detalles mecánicos cuánticos exactos de cómo interactúan los espines.

  • Dado que la interacción espín-espín surge entre dos espines, tenemos que sumar sobre pares de sitios para encontrar su interacción total con la energía.

Más sobre el término de interacción

Una pregunta natural sobre el término de interacción espín-espín es ¿qué espines están acoplados a qué espines?

Si volvemos a la imagen física del imán, y nos acercamos a algún espín en particular, esperaríamos que la fuerza de la interacción espín-espín fuera más fuerte para los espines cercanos y más débil para los espines lejanos. La dependencia exacta de la distancia de las interacciones espín-espín es probablemente bastante complicada para los imanes reales.

Para el modelo de Ising, hacemos la suposición más simple posible para la naturaleza de esta interacción espín-espín:

Algunos comentarios:

• En una red cuadrada de dimensiones, cada sitio tiene 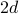vecinos más cercanos: a la izquierda y a la derecha en una dimensión, arriba y abajo una vez que se añade la segunda dimensión, etc…

• Suponemos que la interacción es isotrópica – todos los vecinos son tratados por igual independientemente de la dirección.

• A menudo hablamos de las interacciones vecino más cercano como la energía de un enlace que une dos sitios de la red.

• Cuando estamos sumando sobre pares de sitios adyacentes, simbólicamente, escribimos pequeños paréntesis angulares alrededor de los índices para representar »vecino más cercano».

Una buena consecuencia de las interacciones de vecino más cercano es que cuando estamos encontrando la energía total de alguna configuración de espines, en lugar de sumar sobre todos los posibles pares de sitios, sólo sumamos sobre los pares de sitios que son adyacentes entre sí.

Ahora que hemos discutido todas estas cosas, estamos listos para escribir la expresión real para el Hamiltoniano. (Quería explicar e interpretar la física antes de escribir el Hamiltoniano para que los símbolos tuvieran algún tipo de sentido.)

Hamiltoniano del Modelo de Ising

El Hamiltoniano del Modelo de Ising se puede escribir como

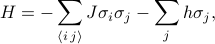
donde representa la interacción espín-espín, representa el campo externo, y los 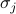son los espines individuales en cada uno de los sitios de la red. La primera suma es sobre todos los pares de sitios de red vecinos (también conocidos como enlaces); representa las interacciones entre espines. La segunda suma es sobre todos los sitios de la red en sí mismos; representa el campo externo tratando de alinear todos los espines en una dirección.

Continuar con la termodinámica del modelo de Ising.