Nežádoucí konvoluce je přirozeným problémem při přenosu analogových informací. Jako konvoluci lze modelovat například všechny následující jevy: rozmazání obrazu u roztřesené kamery, ozvěny při dálkových telefonních hovorech, nekonečná šířka pásma analogových senzorů a elektroniky atd. Dekonvoluce je proces filtrování signálu za účelem kompenzace nežádoucí konvoluce. Cílem dekonvoluce je obnovit signál tak, jak existoval předtím, než došlo ke konvoluci. To obvykle vyžaduje, aby byly známy charakteristiky konvoluce (tj. impulsní nebo frekvenční odezva). To lze odlišit od slepé dekonvoluce, kde charakteristiky parazitní konvoluce nejsou známy. Slepá dekonvoluce je mnohem složitější problém, který nemá obecné řešení a přístup musí být přizpůsoben konkrétní aplikaci.
Dekonvoluci je téměř nemožné pochopit v časové oblasti, ale ve frekvenční oblasti je poměrně jednoduchá. Každá sinusoida, která tvořípůvodní signál, může mít při průchodu nežádoucí konvolucí změněnou amplitudu a/nebo fázi. Aby bylo možné získat původní signál, musí dekonvoluční filtr tyto změny amplitudy a fáze zrušit. Například
, pokud konvoluce změní amplitudu sinusoidy o 0,5 s fázovým posunem 30 stupňů, musí dekonvoluční filtr zesílit sinusoidu o 2,0 se změnou fáze o -30 stupňů.
Příklad, který použijeme k ilustraci dekonvoluce, je detektor gama záření. Jak je znázorněno na obr. 17-3, toto zařízení se skládá ze dvou částí, scintilátorua detektoru světla. Scintilátor je speciální typ průhledného materiálu, jako je jodid sodný nebo germanát vizmutitý. Tyto sloučeniny mění energii každého záření gama na krátký záblesk viditelného světla. Toto světlo
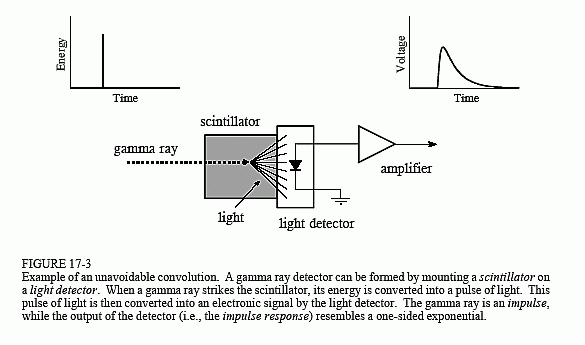
se pak převádí na elektronický signál pomocí detektoru světla, například fotodiody nebo fotonásobiče. Každý impuls vytvořený detektorempředstavuje jednostrannou exponenciálu s určitým zaoblením rohů. Tento tvar je dán vlastnostmi použitého scintilátoru. Když agamma paprsek vloží svou energii do scintilátoru, okolní atomy jsou excitovány na vyšší energetickou hladinu. Tyto atomy náhodně deexcitují, přičemž každý z nich produkuje jeden foton viditelného světla. Výsledkem je světelný puls, jehož amplituda se rozpadá v průběhu několika set nanosekund (pro jodid sodný). Protože příchod každého paprsku gama je impuls, výstupní impuls z detektoru (tj. jednostrannáexponenciála) je impulsní odezvou systému.
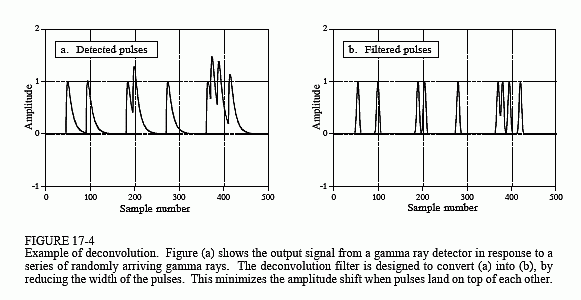
Obrázek 17-4a ukazuje impulsy generované detektorem v reakci na náhodně přicházející záření gama. Informace, kterou bychom chtěli z tohoto výstupního signálu získat, je amplituda každého impulsu, která je úměrná energii paprsku gama, který jej generoval. To je užitečná informace, protože energie může vypovídat o tom, kde se paprsek gama nacházel. Může například poskytnout lékařské informace o pacientovi, říci stáří vzdálené galaxie, odhalit bombu v zavazadle letecké společnosti atd.
Všechno by bylo v pořádku, kdyby bylo detekováno pouze příležitostné záření gama, ale tak tomu obvykle není. Jak ukazuje obrázek (a), dva nebo více pulzů se mohou překrývat, což posouvá naměřenou amplitudu. Jednou z odpovědí na tento problém je dekonvoluce výstupního signálu detektoru, čímž se pulsy zúží, takže dojde k menšímu hromadění. V ideálním případě bychom chtěli, aby se každý impuls podobal původnímu impulsu. Jak asi tušíte, není to možné a musíme se spokojit s impulsem, který má konečnou délku, ale je výrazně kratší než detekovaný impuls. Tento cíl je znázorněn na obr. 17-4b.
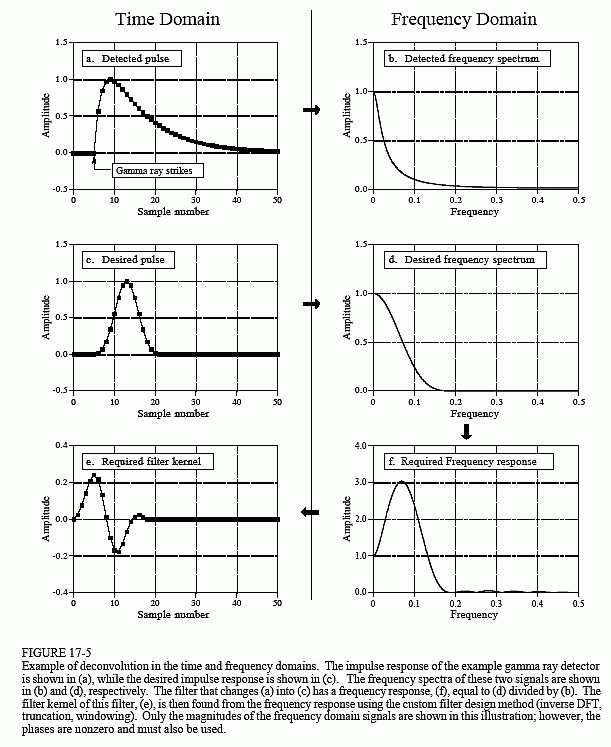
Přestože signál detektoru má svou informaci zakódovanou v časové oblasti,většinu naší analýzy musíme provést ve frekvenční oblasti, kde je problém snáze pochopitelný. Na obrázku 17-5a je signál produkovaný detektorem(něco, co známe). Na obrázku c) je signál, který si přejeme mít (také něco, co známe). Tento požadovaný impulz byl libovolně zvolen tak, aby měl stejný tvar jako Blackmanovo okno s délkou přibližně jedné třetiny původního impulzu. Naším cílem je najít jádro filtru (e), které po konvolování se signálem v bodě (a) vytvoří signál v bodě (c). Ve tvaru rovnice: jestliže a * e = c, a vzhledem k a a c, najděte
Pokud by se tyto signály kombinovaly sčítáním nebo násobením namísto konvoluce, řešení by bylo snadné: odečítání se používá k „odčítání“ a dělení se používá k „násobení“. Konvoluce je jiná; neexistuje jednoduchá inverzní operace, kterou by bylo možné nazvat „dekonvolucí“. Konvoluce je příliš chaotická, než aby se dala zrušit přímou manipulací se signály v časové oblasti.
Naštěstí je tento problém jednodušší ve frekvenční oblasti. Nezapomeňte,že konvoluce v jedné doméně odpovídá násobení v druhé doméně. Opět se odkazujeme na signály na obr. 17-5: jestliže b × f = d a jsou-li dány b a d, najděte f. Řešení tohoto problému je snadné: frekvenční odezva filtru, (f), je frekvenční spektrum požadovaného impulsu, (d), děleno frekvenčním spektrem detekovaného impulsu, (b). Protože detekovaný impuls je asymetrický, bude mít nenulovou fázi. To znamená, že je třeba použít komplexní dělení(tj. velikost & fáze dělená jinou velikostí & fáze). Pokud jste zapomněli, kapitola 9 definuje, jak provést komplexní dělení jednoho spektra druhým. Potřebné jádro filtru, (e), je pak nalezeno z frekvenční odezvy pomocí vlastní metody filtrování (IDFT, posun, zkrácení, &násobení oknem).
Existují limity zlepšení, které může dekonvoluce poskytnout. Jinými slovy, pokud budete chamtiví, věci se rozpadnou. Chamtivost v tomto příkladuznamená snahu o přílišné zúžení požadovaného impulsu. Podívejme se, co se stane. Pokud požadovaný impulz zúžíme, musí jeho frekvenční spektrum obsahovat více vysokofrekvenčních složek. Protože tyto vysokofrekvenčnísložky mají v detekovaném impulsu velmi nízkou amplitudu, musí mít filtr na těchto frekvencích velmi vysoké zesílení. Například (f) ukazuje, že některé frekvence musí být násobeny trojnásobkem, aby bylo dosaženo požadovaného impulsu v (c). Pokud se požadovaný impuls zúží, bude zisk dekonvolučního filtru na vysokých frekvencích ještě větší.
Problémem je, že malé chyby jsou v této situaci velmi nešetrné. Pokud je například některá frekvence zesílena o 30, když je požadováno pouze 28, dekonvolvovanýsignál bude pravděpodobně v nepořádku. Když se dekonvoluce posune na vyššíúrovněvýkonu,musíbýtcharakteristikynežádoucíkonvolucepochopeny s větší přesností a precizností. V reálných aplikacích vždy existují neznámé, způsobené takovými zlosyny, jako jsou: elektronický šum, teplotní drift, rozdíly mezi zařízeními atd. Tyto neznámé omezují, jak dobře bude dekonvoluce fungovat.
I když je nežádoucí konvoluce dokonale pochopena, stále existuje faktor, který omezuje výkon dekonvoluce: šum. Například většina nechtěných konvolucí má podobu dolnopropustného filtru, který snižujeamplitudu vysokofrekvenčních složek v signálu. Dekonvoluce to koriguje zesílením těchto frekvencí. Pokud však amplituda těchto složek klesne pod úroveň vlastního šumu systému, informace obsažená v těchto frekvencích se ztratí. Žádné zpracování signálu je nemůže obnovit. Je navždy ztracena. Adios! Sbohem! Sayonara! Snaha získat tato data zpět jen zesílí šum. V extrémním případě může být amplituda některýchfrekvencí zcela snížena na nulu. Tím se nejen vymažou informace, ale dekonvoluční filtr se bude snažit, aby měl na těchto frekvencích nekonečné zesílení. Řešení: navrhněte méně agresivní dekonvoluční filtr anebo stanovte omezení, jak velké zesílení je povoleno na některé z frekvencí.
Jak daleko můžete zajít? Jak chamtivé je příliš chamtivé? To zcela závisí na problému, na který útočíte. Pokud se signál chová dobře a má nízký šum, lze pravděpodobně dosáhnout významného zlepšení (uvažujte o násobku 5-10). Pokud se signál mění v čase, není zvlášť dobře pochopen nebo je zašuměný, nedosáhnete zdaleka tak dobrých výsledků (uvažujte faktor 1-2). Úspěšná dekonvoluce zahrnuje velké množství testů. Pokud to na určité úrovni funguje, zkuste jít dál; poznáte, kdy se to rozpadne. Žádná teoretická práce vám neumožní tentoiterativní proces obejít.
Dekonvoluci lze také použít na signály zakódované ve frekvenční oblasti. Klasickým příkladem je restaurování starých nahrávek slavného operního pěvce,Enrica Carusa (1873-1921). Tyto nahrávky byly pořízeny na moderní poměry velmi primitivnímzařízením. Nejvýznamnějším problémem jsou rezonance dlouhého trubkového nahrávacího rohu, který se používal ke sběru zvuku. Kdykoli zpěvák zasáhne některou z těchto rezonančních frekvencí, hlasitost nahrávky se náhle zvýší. Digitální dekonvolucezlepšila subjektivní kvalitu těchto nahrávek tím, že
snížila hlasitá místa v hudbě. Popíšeme pouze obecnou metodu;podrobný popis naleznete v původním článku: Stockham, T. Cannon aR. Ingebretsen, „Blind Deconvolution Through Digital Signal Processing“,Proc. IEEE, sv. 63, duben 1975, str. 678-692.
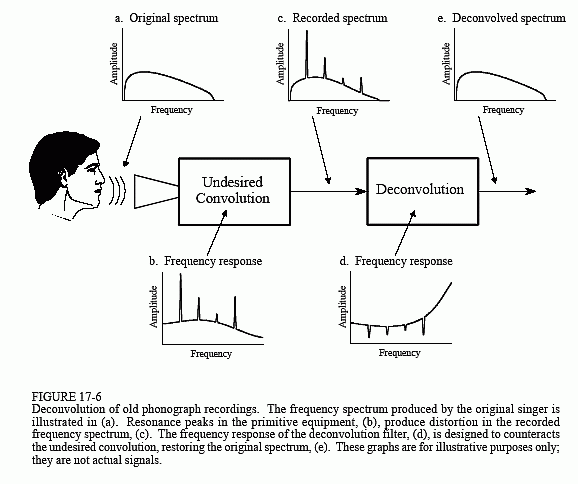
Obrázek 17-6 ukazuje obecný přístup. Frekvenční spektrum původního zvukového signálu je znázorněno v bodě (a). Na obrázku (b) je znázorněna frekvenční odezva záznamového zařízení, poměrně hladká křivka s výjimkouněkolika ostrých rezonančních špiček. Spektrum zaznamenaného signálu, znázorněné na obrázku (c), se rovná skutečnému spektru, (a), vynásobenému nerovnoměrnou frekvenční odezvou, (b). Cílem dekonvoluce je potlačit nežádoucíkonvoluci. Jinými slovy, frekvenční odezva dekonvolučního filtru,(d), musí být inverzní k (b). To znamená, že každý vrchol v (b) je zrušen odpovídajícím poklesem v (d). Kdyby byl tento filtr dokonale navržen, měl by výsledný signál spektrum (e) shodné se spektrem původního signálu.
Tady je háček: původní záznamové zařízení bylo již dávno zlikvidováno a jeho frekvenční charakteristika (b) je záhadou. Jinými slovy, jedná se o problém slepé dekonvoluce; máme-li k dispozici pouze (c), jak můžeme určit (d)?
Problémy slepé dekonvoluce se obvykle řeší odhadem nebo předpokladem o neznámých parametrech. Pro řešení tohoto příkladu se předpokládá, že průměrné spektrum původní hudby odpovídá průměrnému spektru téže hudby v podání současného zpěváka s použitím moderního vybavení. Průměrné spektrum se zjistí technikou uvedenou v kapitole 9:signál se rozdělí na velký počet segmentů, pro každý segment se vezme DFT, převede se do polárního tvaru a pak se velikosti zprůměrují dohromady. Vnejjednodušším případě se neznámá frekvenční charakteristika bere jako průměrné spektrum staré nahrávky dělené průměrným spektrem moderní nahrávky. (Metoda použitá Stockhamem a kol. je založena na sofistikovanější technicezvané homomorfní zpracování, která poskytuje lepší odhadcharakteristik záznamového systému).