Inspirováni podobností s plavci s nízkým Reynoldsovým číslem v tekutinách jsme vytvořili první teorii odporových sil pro zrnitá média k předpovědi sil a pohybu. Klíčovou myšlenkou je princip superpozice: síly na tělesa a nohy složitého tvaru pohybující se v zrnitém prostředí po libovolné trajektorii lze dobře aproximovat superpozicí sil na jednotlivé jejich prvky (obr. 1). Princip integrace platí pro plavce s nízkou Reynoldsovou rychlostí, protože vzhledem k tomu, že setrvačné vlivy jsou zanedbatelné, proudění tekutiny kolem prvků je natolik lokální, že síla působící na prvek granulátu je nezávislá na síle působící na ostatní prvky. Vzhledem k tomu jsme předpokládali, že teorie odporových sil bude fungovat i pro zrnitá prostředí.

Obrázek 1. Princip superpozice teorie odporových sil.
Měření odporových sil
Protože zvířata a roboti mají složitou morfologii a kinematiku, jednotlivé prvky jejich těl a nohou mohou být nejen v různých hloubkách, ale mohou mít také různou orientaci a směr pohybu (obr. 1 vlevo). Pro plavce s nízkým Reynoldsovým číslem v kapalinách lze ze Stokesova zákona odvodit, jak síla závisí na orientaci a směru. Pro zrnitá média však nevíme, jak na nich síla závisí, protože žádné takové rovnice neexistují. Proto jsme pomocí deskového prvku provedli první měření granulární síly v závislosti na orientaci a směru vetřelce (obr. 1, vpravo).
Zjistili jsme, že síla (napětí) citlivě závisí na orientaci i směru (obr. 2, vlevo). Svislá síla je maximální, když je narušitel desky orientován vodorovně a proniká dolů. Jakmile se orientace odchýlí od horizontální a směr se odchýlí od směru dolů, vertikální síla rychle klesá.
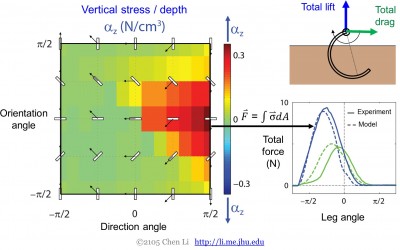
Obrázek 2: Síla, která působí na vnikající prvek. Měření odporové síly a ověření teorie. Pro zjednodušení jsou zobrazena pouze vertikální měření odporových sil.
Ověření teorie odporových sil
Na základě našich měření odporových sil v granulích jsme integrovali napětí na prvcích nohy a zjistili, že teorie odporových sil dokáže dobře předpovědět celkové vztlakové a odporové síly na noze robota pohybující se v granulovaném prostředí (obr. 2 vpravo). Díky principu superpozice je model přesný pro nohy libovolného tvaru a trajektorie:
Predikční schopnost teorie odporových sil
Po ověření teorie odporových sil na noze robota otáčející se přes zrnité prostředí (předepsaná kinematika) jsme dále testovali její predikční schopnost na robotovi volně se pohybujícím po zrnitém prostředí. Spustili jsme robota s vlastní nohou na granulovaném médiu s širokým rozsahem frekvence kroku a zakřivení nohy. Jak jsme již dříve zjistili, robot se pohybuje rychleji s nohama s konvexním povrchem směřujícím dozadu než dopředu:
Poté jsme vytvořili dynamickou simulaci robota s více tělesy a použili jsme teorii odporových sil k výpočtu vztlakových a odporových sil na těle a nohách robota integrací elementárních sil. Zjistili jsme, že dynamika pohybu předpovězená simulací pomocí teorie odporových sil dobře odpovídá experimentálnímu pozorování:
Srovnání experimentu a simulace ukázalo, že teorie odporových sil dokáže přesně a rychle předpovědět lokomoci nohou na zrnitém prostředí v širokém rozsahu krokové frekvence a zakřivení nohou (obr. 3).
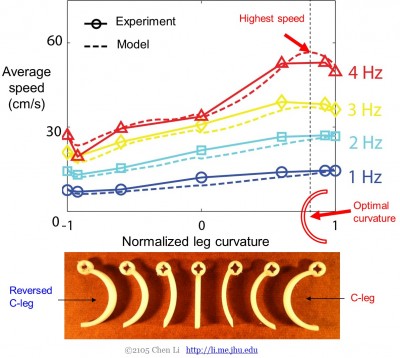
Obr. 3. Dynamika pohybu nohou na zrnitém prostředí. Teorie odporových sil předpovídá pohyb nohou robota na zrnitém prostředí.
Protože naše teorie odporových sil umožnila kvantitativní předpověď sil a pohybu v zrnitém prostředí analogicky k aero- a hydrodynamice pro tekutiny, vytvořili jsme první terradynamika proudícího terénu.
Všeobecnost teorie odporových sil
Provedli jsme měření odporových sil pro různorodá zrnitá média s různou velikostí částic, tvarem, třením, hustotou, zhutněním a polydisperzitou. Zjistili jsme, že závislost síly na orientaci a směru vměstku je nápadně podobná (obr. 4, vlevo).
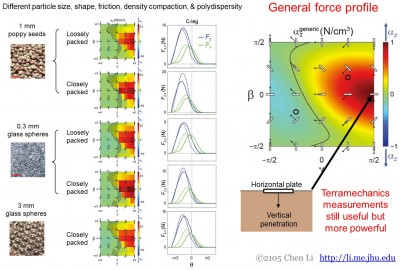
Obrázek 4. Obecnost teorie odporové síly pro různorodá zrnitá média a její praktický přínos.
To poskytuje významný praktický přínos. Protože tato zrnitá média mají stejný obecný profil napětí, stačí jediné měření síly pro určení maximální vertikální síly, aby bylo možné odvodit síly pro ostatní orientace a směry, aniž by bylo nutné měřit všechny (obr. 4 vpravo). To lze jednoduše provést pomocí běžně dostupného penetrometru. To také znamená, že měření pomocí horizontální desky penetrující směrem dolů získaná v terramechanických studiích lze stále využít, ale s větší silou pomocí teorie odporových sil.
Nakonec, díky principu superpozice lze naši teorii odporových sil v zásadě aplikovat na zvířata a zařízení libovolné morfologie a kinematiky (za předpokladu, že pracují v režimech nízkých rychlostí, neinerciálních a kontinuálních). Zjistili jsme například také, že teorie využívající měření odporových sil v horizontální rovině dokáže předpovědět pohyb ještěrky písečné v zrnitém prostředí.
Proč klasická terramechanika selhává u marsovských vozítek
V klasické terramechanice, protože velká kola a pásy mají obvykle relativně ploché a rovné rozhraní terénu, jsou vertikální vnikací síly v zrnitém prostředí charakterizovány pouze pohybem vodorovné desky směrem dolů (pomocí penetrometru) (Obr. 5), ale ne na vniknutí v jiných směrech a orientacích. Toho se pak využívá k předpovědi vztlaku, který se následně vyváží (staticky a dynamicky) s hmotností vozidla k předpovědi propadání.
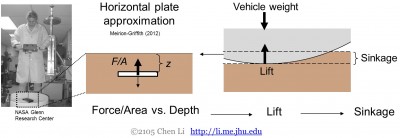
Obrázek 5. Aproximace horizontální desky převládající při vývoji klasických terramechanických modelů.
U malých kol roverů pohybujících se po sypkém zrnitém prostředí (nebo i u větších kol zapuštěných dostatečně hluboko) se však rozhraní půdy stává silně zakřiveným s orientací daleko od horizontální. Jak jsme ukázali pomocí našich měření odporových sil, která zohledňují všechny orientace a směry, na vodorovnou desku obecně působí mnohem větší svislá síla než na desku vzdálenou od vodorovné polohy (obr. 2 vlevo). V důsledku toho aproximace horizontální desky již neplatí a klasické terramechanické modely podstatně nadhodnocují předpověď vztlakové síly a podhodnocují potopení.
Související publikace:
- Li C, Zhang T, Goldman DI (2013). A terradynamics of legged locomotion on granular media, Science, 339, 1408-1412 (Featured in Science Perspective) PDF
- Ding, Y, Li C, Goldman DI (2013). Plavání v poušti, Physics Today, 66, 68-69 (Pozvaný příspěvek) PDF
- Maladen RD, Ding Y, Li C, Goldman DI (2009). Undulatory swimming in sand: subsurface locomotion of the sandfish lizard (Vlnovité plavání v písku: podpovrchová lokomoce ještěra písečného), Science, 325, 314-318 (publikováno v Nature News & Views) PDF
.