Jak vypočítat napětí v lanech zavěšujících předmět

Na obrázku níže vidíme, že síla F potřebná ke zvednutí předmětu je rovna hmotnosti předmětu W. Tato myšlenka je základním konceptem, ze kterého vychází náš vzorec pro sílu tahu. Níže je také znázorněn diagram volného tělesa předmětu, který ukazuje tahové síly, T, působící v provázku. Jak vidíte, tahové síly přicházejí ve dvojicích a v opačných směrech:

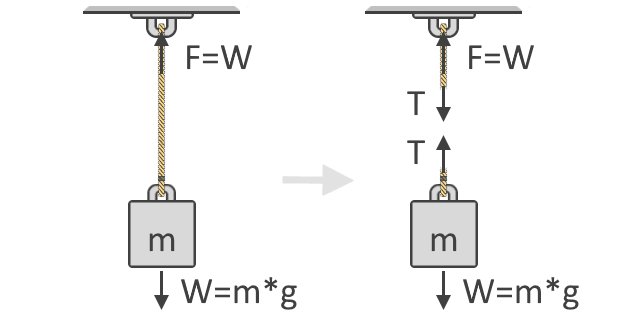
Podle druhého Newtonova pohybového zákona pak můžeme součet sil vyjádřit pomocí diagramu volného tělesa předmětu, jak je znázorněno na pravé straně obrázku výše. Diagramy volných těles používáme k zobrazení různých směrů a velikostí sil, které na těleso působí. V rovnovážném stavu by se všechny tyto síly měly rovnat nule. Uvažujeme-li všechny síly směřující nahoru jako kladné a dolů jako záporné, naše rovnice zní:

ΣF = 0 = T + (-W)
T = W
kde hmotnost, W, se stává zápornou, protože směřuje dolů. Přenesením W na druhou stranu rovnice nyní vidíme, že tahová síla v laně je rovna hmotnosti předmětu, který nese, jak je také uvedeno výše.

Použijeme-li ke zvedání předmětu více lan, celková tahová síla se rozdělí na jednotlivá lana. Tahová síla v jednotlivých lanech závisí na jejich úhlech vzhledem ke směru síly, které odporují. Abychom tomu lépe porozuměli, uvažujme další diagram volného tělesa předmětu zavěšeného na dvou lanech, jak je znázorněno níže:

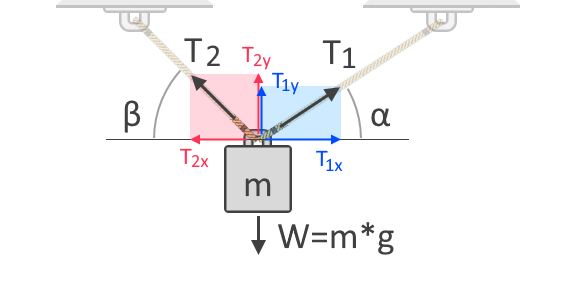
V diagramu volného tělesa znázorněném výše vidíme vodorovné a svislé složky tahových sil, T₁ a T₂. Síly jsou vektory, což znamená, že mají vždy jak velikost, tak směr. Jako všechny vektory lze i síly vyjádřit v těchto složkách, které udávají působení síly podél vodorovné a svislé osy. T₁ₓ a T₂ₓ jsou svislé složky T₁ a T₂. Na druhé straně T₁ᵧ a T₂ᵧ jsou svislé složky stejných sil. Protože gravitace působí na objekt ve svislé ose, musíme pro náš součet sil uvažovat svislé složky tahových sil takto:

ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)
W = T₁ᵧ + T₂ᵧ

Protože známe i úhly tahových sil, můžeme T₁ᵧ a T₂ᵧ vyjádřit pomocí trigonometrických funkcí:

T₁ᵧ = T₁ * sin(α)
T₂ᵧ = T₂ * sin(β)
W = T₁ * sin(α) + T₂ * sin(β)

Můžeme také říci, že aby byla soustava v rovnováze, neměl by se objekt pohybovat ve vodorovném směru ani podél osy x. V případě, že je soustava v rovnováze, nesmí se pohybovat podél osy x. Proto se pak horizontální složky T₁ a T₂ musí rovnat nule. Také s pomocí trigonometrie můžeme vyjádřit T₁ₓ a T₂ₓ v termínech T₁ a T₂:

T₁ₓ = T₂ₓ
T₁ * cos(α) = T₂ * cos(β)

Vydělíme-li obě strany cos(α), dostaneme rovnici, v níž je T₁ vyjádřeno v termínech T₂ a úhlů:

T₁ = T₂ * cos(β) / cos(α)

Tuto rovnici pak můžeme použít k řešení T₂ tak, že do naší rovnice součtu sil dosadíme T₂ * cos(β) / cos(α) jako T₁, jak je uvedeno níže:

W = T₁ * sin(α) + T₂ * sin(β)
W = T₂ * * sin(α) + T₂ * sin(β)
W = T₂ *
T₂ = W /

Nakonec, pokud celou tuto rovnici vynásobíme cos(β) / cos(α), jak jsme odvodili v hodnotě T₁ z hlediska T₂, a poté vše zjednodušíme, dostaneme tuto rovnici:

T₁ = W / *
T₁ = W / *
T₁ = W /

Teď už stačí znát jen úhly napínacích lan vzhledem k vodorovné rovině. Je-li dán úhel od svislice, stačí tento úhel odečíst od 90°. Tím získáte úhel od vodorovné roviny. Pokud jsou však zadány jiné hodnoty úhlů, které mohou být větší než 90° nebo dokonce 180°, můžete se podívat na naši kalkulačku referenčních úhlů, která vám pomůže určit potřebný úhel. Po určení hodnot proměnných v našich vzorcích pro tahové síly můžeme nyní řešit tahové síly.

.