Nula je číslo, které se na číselné řadě nachází přesně mezi kladnými a zápornými čísly. Nula je považována za celé číslo spolu s kladnými přirozenými čísly (1, 2, 3, 4…) a zápornými čísly, (…-4,-3,-2,-1).

Nula je zvláštní číslo v řadě celých čísel, protože je to jediné celé číslo, které není ani kladné, ani záporné. Je to také jediné celé číslo, které není ani prvočíslo, ani složené číslo. Je považováno za sudé číslo, protože je dělitelné dvěma beze zbytku. Nula je aditivním prvkem identity v různých systémech algebry a číslice „0“ se používá jako zástupná hodnota v systémech pozičního zápisu pro reprezentaci čísel.

Nula má mnoho zajímavých vlastností, díky kterým je pro matematiky zajímavá. Pokud přičtete nebo odečtete nulu od libovolného čísla, číslo zůstane stejné Pokud vynásobíte nulu libovolným číslem, výsledkem je 0. Každé číslo zvýšené na nultou (0.) mocninu je 1, takže 20=1 a 560=1. V tradiční algebře je dělení nulou nedefinované, takže žádné číslo nelze dělit nulou. Číslo 0 je také prvkem reálných čísel a komplexních čísel.

Historie čísla 0

Kde se vzala myšlenka nuly? V dnešní době se nám zdá intuitivní; nula je číslo, které označuje nulovou veličinu – nic. Nuly vidíme všude ve společnosti a přirozeně chápeme, co znamenají a jak s nimi lze matematicky manipulovat. Historicky však trvalo poměrně dlouho, než byl pojem 0 všeobecně uznán jako předmět matematiky, a mnozí v průběhu dějin tvrdili, že číslo nula neexistuje nebo že myšlenka nuly je nesourodý pojem.

Mnohé starověké společnosti neměly explicitní pojem nulové veličiny ani konkrétní číslici, kterou by používaly pro její reprezentaci. Staří Egypťané i Babyloňané měli určitou představu o nulové veličině a potřebu zástupných hodnot při reprezentaci čísel, ale nikdy nevytvořili výraznou číslici nebo pojem, který by tuto veličinu nebo zástupnou hodnotu reprezentoval. Staroegyptské číselné systémy byly výhradně obrázkové a neměly poziční hodnoty, zatímco starověcí Babyloňané používali mezery mezi čísly k reprezentaci pozičních hodnot.

Májové měli explicitní pojem 0 a měli samostatnou číslici, která tento pojem reprezentovala a používala jako poziční hodnotu v jejich vigesimálním (základ 20) kalendářním systému. Ačkoli mayská, olmécká a další předkolumbovské společnosti byly jedny z prvních v historii, které měly explicitní a propracované chápání čísla 0, tyto systémy dále neovlivnily společnosti Starého světa v Evropě.

Složitý vztah k nule měli naopak staří Řekové. Neměli symbol pro její pojem ani pro ni jako zástupnou hodnotu, protože si nebyli jisti, zda lze číslo 0 považovat za skutečně existující věc. Ptali se, jak může být něco (číslo) ničím (nulou)? Pro Řeky byla přirozená čísla (1, 2, 3, 4,…) odvozena z našeho chápání jednotlivých diskrétních objektů ve světě. Sám Aristoteles slavně tvrdil, že 0 neexistuje, s odůvodněním, že 0 představuje prázdnotu nebo nicotu a skutečná prázdnota nebo nicota nemůže existovat.

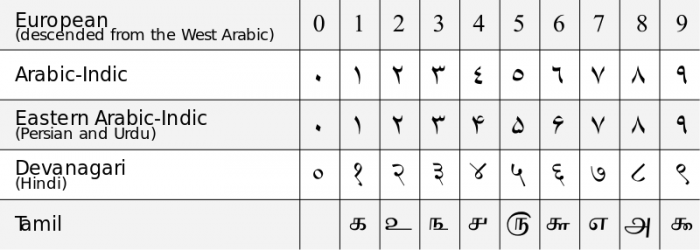
Číňané chápali „0“ jako zástupnou číslici pro své počítací systémy, ale nepovažovali číslici „0“ za představitele nějakého samostatného čísla, pouze za užitečný symbol. Běžné chápání 0 jako samostatného čísla a jako číslice pro poziční notační systémy přišlo z Indie v průběhu 6. století našeho letopočtu. Indičtí matematici v té době vyvinuli první druhy desítkových (základ 10) notačních systémů, které zahrnovaly 0 jako samostatnou číslici a měly pochopení pro jedinečné matematické vlastnosti nuly. V 11. století n. l. se myšlenka nuly rozšířila do západní Evropy vlivem islámských matematiků žijících ve Španělsku pod vládou Umajjovského chalífátu a vznikl moderní arabský číselný systém desítkového zápisu. První použití anglického slova „zero“ se datuje do roku 1589.

Matematické vlastnosti nuly

Nulové číslo hraje nedílnou roli téměř ve všech oblastech matematiky. Nula je nejmenší nezáporné celé číslo a nemá žádné přirozené číslo, které by z ní vycházelo. Protože nula je celé číslo, je také racionálním číslem, reálným číslem a komplexním číslem. V matematice je 0 považována za veličinu, která odpovídá nulovému množství. Dalo by se říci, že nula je „množství“, které má množina, jež nemá žádné členy.

V algebře

V elementární algebře se nula často vyjadřuje tak, že leží ve středu číselné přímky. Číslo 0 se považuje za sudé číslo, protože je celočíselným násobkem čísla 2 (2×0=0). 0 není prvočíslo, protože má nekonečné množství činitelů, a není ani složené číslo, protože žádný součin dvou prvočísel se nerovná číslu 0.

Vzhledem ke 4 hlavním aritmetickým operátorům (+, -, ×, ÷) a operaci exponentu se číslo 0 chová podle následujících pravidel:

• Sčítání: x+0=0+x=x . Nula je považována za aditivní prvek identity, protože jakékoli číslo plus nebo minus nula se rovná tomuto číslu
• Subtrakce: x-0=x a 0-x=-x
• Multiplikace: x⋅0=0⋅x=0. Jakékoli číslo vynásobené 0 je rovněž rovno 0.
• Dělení: 0/x=0, kromě případů, kdy x=0. x/0 je matematicky nedefinovaná veličina, protože 0 nemá žádnou multiplikativní inverzi (žádné číslo vynásobené 0 nedává 1).
• Exponenty: x0=1, kromě případů, kdy x=0. Dlouho se diskutovalo o tom, zda je 00 nedefinovaný, nebo dobře utvořený výraz. Pro všechna kladná x platí 0x=0.

Ve výrazech zahrnujících limity se veličina 0/0 může objevit v souvislosti s demonstrací limit racionálních funkcí typu f(x)/g(x). V těchto případech není 0/0 neurčitá, ale představuje neurčitý tvar. To neznamená, že limita je neurčitá, ale že je třeba ji vypočítat jinou metodou, například nalezením derivace. Existují některé algebraické modely, kde dělení nulou dává definovanou veličinu, například projektivně prodloužená reálná přímka nebo Riemannova sféra.

V teorii množin

V teorii množin číslo 0 odpovídá kardinalitě „prázdné množiny“ nebo „nulové množiny“ (běžně reprezentované jako {} nebo {∅}. Kardinalita množiny je množství prvků v této množině, pokud v ní nemáme žádné pomeranče, pak máme množinu 0 pomerančů (prázdnou množinu pomerančů).

Nula se v teorii množin často používá jako výchozí bod pro konstrukci ostatních přirozených čísel. Tyto von Neummanovy konstrukce, pojmenované po slavném polyhistorovi Johnu von Neumannovi, konstruují přirozená čísla definicí 0={} a definují následnickou funkci S(a) = a ∪ {a}. Celá přirozená čísla lze zkonstruovat z rekurzivních aplikací následnické funkce počínaje prázdnou množinou:

0 = {}

1 = 0 ∪ {0} = {0} = {{}}

2 = 1 ∪ {1} = {0,1} = {{}, {{}}}

3 = 2 ∪ {2} = {0, 1, 2} = {{}, {{}, {{}, {{}}}}

a tak dále. Podle tohoto vzoru lze sestrojit celou nekonečnou množinu přirozených čísel. Tímto způsobem můžeme říci, že každému přirozenému číslu odpovídá množina obsahující všechna přirozená čísla před ním.

Ve fyzice

V souvislosti s prováděním kvantitativních měření ve fyzice je 0 považována za základní hodnotu, od níž se odvíjejí všechna ostatní měření jednotek. Velmi často odpovídá základní hodnota 0 nějaké fyzikálně významné veličině, která je přirozeně odlišitelná od všech ostatních veličin měření.

Například v Kelvinově stupnici odpovídá teplota 0 K absolutní 0 – nejchladnější teplotě, která je fyzikálně možná. V Celsiově teplotní stupnici je 0 °C definována jako bod tuhnutí vody při atmosférickém tlaku. V kontextu dynamiky a elektromagnetismu je hodnota 0 dána poloze, ve které má systém minimální možné množství potenciální energie. Například základnímu stavu atomu, nejnižší možné energetické hladině pro elektrony v atomu, se často přiřazuje hodnota 0.

Podobně v kontextu kinematiky je vztažná soustava, ze které se provádí pozorování pohybu, definována jako soustava se středem ležícím na počátku souřadnicové osy v bodě (0, 0). V případě zachovávaných veličin, jako je hmotnost-energie, hybnost a úhlový moment, je celková velikost změny zachovávaných veličin v izolované soustavě vždy rovna 0.

V informatice

Počítače uchovávají informace ve formě bitů-dlouhých posloupností jedniček a nul. V této binární reprezentaci odpovídá 0 poloze „vypnuto“ a je v protikladu k poloze „zapnuto“ označené 1. Hodnota 0 v elektrickém obvodu znamená, že obvod je vypnutý a neprobíhá v něm žádný elektrický tok. Podobně mnoho výpočetních logik definuje „0“ jako znak, který představuje nepravdivou pravdivostní hodnotu.

V počítačových databázích se prvky pole počítají pomocí počítacího systému založeného na nule. To znamená, že pro množinu s n prvky mají prvky indexy začínající číslem 0. Prvek s indexovým číslem 0 je tedy ve skutečnosti prvním prvkem v řadě, indexovému číslu 1 odpovídá druhý prvek atd. Obecně platí, že n-tý člen množiny má indexové číslo odpovídající n-1. Tento systém počítání může způsobit zmatek novým programátorům, kteří jsou zvyklí intuitivně přiřazovat indexové hodnoty začínající číslem 1.