Isingův model je konkrétním příkladem termodynamického systému a je to modelový systém pro pochopení fázových přechodů. Víte, jak mnoho biologů tráví tolik času s mizernými ovocnými muškami? No, fyzikové tráví spoustu času s Isingovým modelem. Jak nám profesor Raghu ochotně říká, je to drozofila fázových přechodů.

Osobně nejsem největším fanouškem jeho přirovnání, protože si myslím, že ovocné mušky jsou nechutné. Doufejme, že Isingův model nebude příliš nechutný.

Motivace

Proč bychom měli trávit tolik času povídáním o Isingově modelu?

• Je překvapivě užitečný, protože nám pomáhá přemýšlet o všech druzích chování souvisejících s fázovými přechody. Například:

  • Isingův model vykazuje porušení symetrie v nízkoteplotní fázi (o kterém jsme právě mluvili)

  • má zvláštní „kritický bod“ při přesně definované teplotě (na který jsme naráželi ve fázovém diagramu vody)

  • další bohaté vlastnosti.

• Je to jeden z mála přesně řešitelných modelů, kde můžeme skutečně vypočítat termodynamické veličiny a interpretovat je.

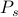  • Všeobecně je výpočet termodynamických veličin obtížný, protože musíme sečíst mnoho členů. Vzpomeňte si z naší první hodiny termiky, že o rovnovážném systému můžete uvažovat jako o souboru mnoha stavů , z nichž každý je zatížen vlastní pravděpodobností . V tomto rámci termodynamické veličiny, které pozorujete, odpovídají průměrům v celém souboru. Konkrétně chcete-li najít průměr souboru nějaké pozorované veličiny 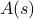, musíte najít součet 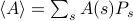, kde součet probíhá přes všechny možné stavy. Problémem je, jak si pamatujete, že počet stavů termodynamického systému se škáluje exponenciálně s počtem částic! I pro středně velký systém je prostě příliš mnoho stavů na to, aby počítač explicitně spočítal průměr – natož pro termodynamický systém, kde je řádově .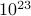

  • Pro výpočet rozdělovací funkce tedy musíme být “chytří“ a měli bychom být vděční za přesně řešitelné systémy!

• Isingův model je jednoduchý, a přesto jej lze aplikovat na překvapivé množství různých systémů.

  • Toto je naše první ochutnávka univerzality – vlastnosti kritických jevů, kdy stejná teorie platí pro všechny druhy různých fázových přechodů, ať už v kapalinách a plynech, nebo v magnetech, supravodičích či čemkoli jiném. Fyzikové tento druh obecného chování milují, protože naznačuje jakýsi hlubší řád v našem chaotickém světě.

Definice Isingova modelu

Isingův model je matematický model, který neodpovídá skutečnému fyzikálnímu systému. Je to obrovská (čtvercová) mřížka míst, kde každé místo může být v jednom ze dvou stavů. Každé místo označíme indexem a tyto dva stavy nazveme a . Chceme-li říci, že -té místo je ve stavu , napíšeme .

Tato definice je žalostně abstraktní a nefyzikální, takže pro nás fyziky je nesmírně užitečné mít na mysli skutečný systém, abychom se mohli odvolávat na něco explicitního a budovat fyzikální intuici. Zde je několik fyzikálních systémů, které by Isingův model mohl reprezentovat:

• Magnet. Každé místo představuje určitý „spin“ v materiálu (nespárovaný elektron??) a je , pokud spin směřuje dolů, nebo , pokud spin směřuje nahoru. Každý ze spinů se chová jako mini magnet s vlastním mini magnetickým momentem; pokud jsou všechny spiny vyrovnané, pak se celá mřížka spinů chová jako velký magnet s čistým makroskopickým magnetickým momentem.

• Slitina; řekněme mosaz. Každé z míst představuje atom v mřížce; představuje atom mědi v daném místě; představuje zinek.

• Mřížkový plyn“. Každé z míst představuje možné umístění částice; znamená, že místo je prázdné, a znamená, že místo je obsazeno částicí.

• Bakteriální vírové mřížky?

Prozatím budeme Isingův model považovat za model magnetu. Je to jistě hrubě zjednodušený a hračkářský model magnetu, ale analogie s magnetem nám přesto může pomoci vést naši ceněnou fyzikální intuici.

Složení Hamiltoniánu

Přirozenou otázkou, kterou si můžeme položit v souvislosti s tímto modelem magnetu ve tvaru Mickeyho myši, je, jakou má energii. Přesněji řečeno, chceme zapsat funkci, která představuje energii každé jednotlivé možné konfigurace (tzv. mikrostavu) spinů v magnetu. Jak víme, tato energetická funkce se nazývá Hamiltonián.

V Isingově modelu zahrnuje Hamiltonián dva typy interakcí:

• člen vnějšího pole. Jak si pamatujeme z kvantové mechaniky, vnější magnetické pole může rozdělit energie stavu spin-down a spin-up, takže jeden má vyšší energii a druhý nižší.

  • Velikost představuje, jak silné je pole, takže říká, o kolik vyšší energii má jeden spin než druhý.

  • Znak říká, zda je preferován spin up nebo spin down.

  • Protože každý jednotlivý spin cítí vnější pole, musíme sečíst všechna místa, abychom zjistili celkový příspěvek k energii.

• interakční člen mezi sousedními spiny – možná se chtějí vzájemně vyrovnat a směřovat stejným směrem, možná se chtějí proti sobě vyrovnat a směřovat různými směry. Fyzikálně si můžeme představit, že tato interakce vzniká proto, že každý spin v magnetu je svým vlastním miniaturním magnetickým dipólem, který nastavuje své vlastní magnetické pole, a jeho sousedé mohou toto magnetické pole cítit.

  • Velikost vypovídá o tom, jak silně jsou sousední spiny navzájem spřaženy – jak moc se chtějí (anti)vyrovnat. Fyzikálně by síla spinové vazby mohla záviset například na vzdálenosti mezi nimi v magnetové mřížce.

  • Značka vám říká, zda se sousedé raději zarovnávají, nebo proti sobě. (Technický termín pro to je feromagnetický, respektive antiferomagnetický). Fyzikálně to, zda je materiál jeden nebo druhý (nebo ani jeden), závisí na přesných kvantově mechanických detailech interakce spinů.

  • Protože spin-spinová interakce vzniká mezi dvěma spiny, musíme sečíst dvojice míst, abychom zjistili její celkovou interakci na energii.

Další informace o členu interakce

Přirozenou otázkou ohledně členu interakce spin-spin je, které spiny jsou spojeny s kterými spiny?

Pokud se opět vrátíme k fyzikálnímu obrazu magnetu a přiblížíme si nějaký konkrétní spin, očekávali bychom, že síla spin-spinové interakce bude silnější pro blízké spiny a slabší pro spiny vzdálené. Přesná závislost spin-spinové interakce na vzdálenosti je u skutečných magnetů pravděpodobně dosti komplikovaná.

Pro Isingův model učiníme nejjednodušší možný předpoklad o povaze této spin-spinové interakce:

Několik poznámek:

• Ve čtvercové mřížce o rozměrech má každé místo 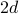nejbližších sousedů: vlevo a vpravo v jednom rozměru, nahoře a dole, jakmile přidáte druhý rozměr, atd…

• Předpokládáme, že interakce je izotropní – se všemi sousedy se zachází stejně bez ohledu na směr.

• O interakci nejbližšího souseda často hovoříme jako o energii vazby, která spojuje dvě místa mřížky.

• Když sčítáme přes sousední dvojice míst, symbolicky píšeme kolem indexů malé hranaté závorky, které představují “nejbližšího souseda“.

Pěkným důsledkem interakcí nejbližšího souseda je, že když zjišťujeme celkovou energii nějaké konfigurace spinů, místo abychom sčítali přes všechny možné dvojice míst, sčítáme pouze přes dvojice míst, které spolu sousedí.

Teď, když jsme všechny tyto věci probrali, jsme připraveni zapsat skutečný výraz pro hamiltonián. (Před zápisem hamiltoniánu jsem chtěl vysvětlit a interpretovat fyziku, aby symboly dávaly nějaký smysl.)

Hamiltonián Isingova modelu

Hamiltonián Isingova modelu lze zapsat jako

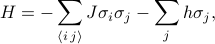
kde představuje interakci spin-spin, představuje vnější pole a 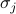jsou jednotlivé spiny na jednotlivých místech mřížky. První součet je přes všechny dvojice sousedních mřížkových míst (neboli vazeb); představuje interakce mezi spiny. Druhý součet je nad všemi mřížkovými místy samotnými; představuje vnější pole, které se snaží vyrovnat všechny spiny v jednom směru.

Pokračujte v termodynamice Isingova modelu.