podle Marco Taboga, PhD
Indikátorová funkce události je náhodná proměnná, která nabývá hodnoty 1, když událost nastane, a hodnoty 0, když událost nenastane. Indikátorové funkce se často používají v teorii pravděpodobnosti pro zjednodušení zápisu a pro důkaz teorémů.

Definice
Následuje formální definice.
Definice Nechť  je výběrový prostor a
je výběrový prostor a  je událost. Indikátorová funkce (neboli indikátorová náhodná veličina) události
je událost. Indikátorová funkce (neboli indikátorová náhodná veličina) události  , označená
, označená  , je náhodná veličina definovaná takto:
, je náhodná veličina definovaná takto: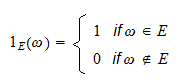
Zatímco indikátor události  se obvykle označuje
se obvykle označuje  , někdy se také označuje
, někdy se také označuje , kde
, kde  je řecké písmeno Chi.
je řecké písmeno Chi.
Příklad Házíme kostkou a jedno ze šesti čísel od 1 do 6 se může objevit lícem nahoru. Vzorový prostor je Definice události
Definice události  popsané větou „Sudé číslo se objeví lícem nahoru“. Náhodná proměnná, která nabývá hodnoty 1, když se sudé číslo objeví lícem nahoru, a hodnoty 0 v opačném případě, je indikátorem události
popsané větou „Sudé číslo se objeví lícem nahoru“. Náhodná proměnná, která nabývá hodnoty 1, když se sudé číslo objeví lícem nahoru, a hodnoty 0 v opačném případě, je indikátorem události  . Případová definice tohoto indikátoru je
. Případová definice tohoto indikátoru je
Z výše uvedené definice lze snadno zjistit, že  je diskrétní náhodná veličina s podporou
je diskrétní náhodná veličina s podporou  a pravděpodobnostní hmotnostní funkcí
a pravděpodobnostní hmotnostní funkcí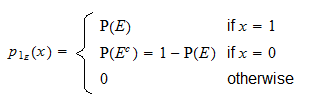
Vlastnosti
Indikátorové funkce mají následující vlastnosti.
Mocniny
 Třetí mocnina
Třetí mocnina  je rovna
je rovna  :
: protože
protože  může být buď
může být buď  nebo
nebo  a
a
Očekávaná hodnota
Očekávaná hodnota  je rovna
je rovna  :
: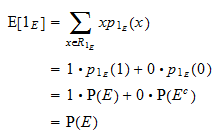
Rozptyl
Rozptyl  je roven
je roven  . Díky obvyklému vzorci pro rozptyl a výše uvedené vlastnosti mocnin dostáváme
. Díky obvyklému vzorci pro rozptyl a výše uvedené vlastnosti mocnin dostáváme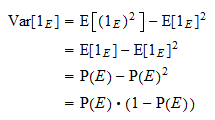
Rozptyl
Jsou-li  a
a  dvě události, pak
dvě události, pak protože:
protože:
-
jestliže
 , pak
, pak  a
a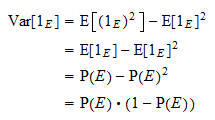
-
jestliže
 , pak
, pak a
a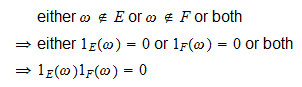
Ukazatele událostí s nulovou pravděpodobností
Nechť  je událost s nulovou pravděpodobností a
je událost s nulovou pravděpodobností a  je integrovatelná náhodná veličina. Potom,
je integrovatelná náhodná veličina. Potom, Ačkoliv rigorózní důkaz této skutečnosti přesahuje rámec tohoto úvodního výkladu, měla by být tato vlastnost intuitivní. Náhodná veličina
Ačkoliv rigorózní důkaz této skutečnosti přesahuje rámec tohoto úvodního výkladu, měla by být tato vlastnost intuitivní. Náhodná veličina  je rovna nule pro všechny výběrové body
je rovna nule pro všechny výběrové body  s výjimkou případně bodů
s výjimkou případně bodů  . Očekávaná hodnota je vážený průměr hodnot, kterých může nabývat
. Očekávaná hodnota je vážený průměr hodnot, kterých může nabývat  , přičemž každá hodnota je vážena příslušnou pravděpodobností. Nenulové hodnoty, kterých
, přičemž každá hodnota je vážena příslušnou pravděpodobností. Nenulové hodnoty, kterých  může nabývat, jsou váženy nulovou pravděpodobností, takže
může nabývat, jsou váženy nulovou pravděpodobností, takže  musí být nula.
musí být nula.
Řešená cvičení
Níže najdete několik cvičení s vysvětleným řešením.
Cvičení 1
Uvažujme náhodnou veličinu  a další náhodnou veličinu
a další náhodnou veličinu  definovanou jako funkce
definovanou jako funkce  .
.
Vyjádřete  pomocí indikačních funkcí událostí
pomocí indikačních funkcí událostí  a
a  .
.
Značte  indikátor události
indikátor události  a označte
a označte  indikátor události
indikátor události  .
.  můžeme zapsat jako
můžeme zapsat jako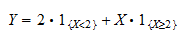
Cvičení 2
Nechť  je kladná náhodná veličina, tj. náhodná veličina, která může nabývat pouze kladných hodnot. Nechť
je kladná náhodná veličina, tj. náhodná veličina, která může nabývat pouze kladných hodnot. Nechť  je konstanta. Dokažte, že
je konstanta. Dokažte, že  kde
kde  je indikátor události
je indikátor události  .
.
Nejprve si všimněte, že součet ukazatelů  a
a  je vždy roven
je vždy roven  :
: V důsledku toho můžeme psát
V důsledku toho můžeme psát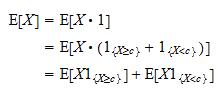 Nyní si všimněte, že
Nyní si všimněte, že  je kladná náhodná veličina a že očekávaná hodnota kladné náhodné veličiny je kladná:
je kladná náhodná veličina a že očekávaná hodnota kladné náhodné veličiny je kladná: Takže,
Takže,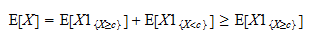
Cvičení 3
Nechť  je událost a její indikační funkci označme
je událost a její indikační funkci označme  . Nechť
. Nechť  je doplněk
je doplněk  a jeho indikační funkci označme
a jeho indikační funkci označme  . Můžete vyjádřit
. Můžete vyjádřit  jako funkci
jako funkci  ?
?
Součet obou ukazatelů je vždy roven  :
: Takže,
Takže,
Jak citovat
Citujte prosím:
Taboga, Marco (2017). „Indikátorové funkce“, Přednášky z teorie pravděpodobnosti a matematické statistiky, třetí vydání. Kindle Direct Publishing. Online příloha. https://www.statlect.com/fundamentals-of-probability/indicator-functions.