Jak provést Guinierovo přizpůsobení?¶
Guinierova aproximace platí pouze tehdy, když je exponenciála \(\exp(-q^2 R_g^2 /3)\)malá. To znamená, že k dobrému Guinierovu přizpůsobení potřebujeme, abyqRg bylo dostatečně malé. Hodnota qRg, při které začíná Guinierova aproximace pro daný profil rozptylu selhávat, závisí na celkovém tvaru rozptylovače. Níže je obrázek znázorňující Guinierovu aproximaci (černě) a intenzitu rozptylu pro kouli, tenkou tyč a tenký disk (všechny se stejným Rg).
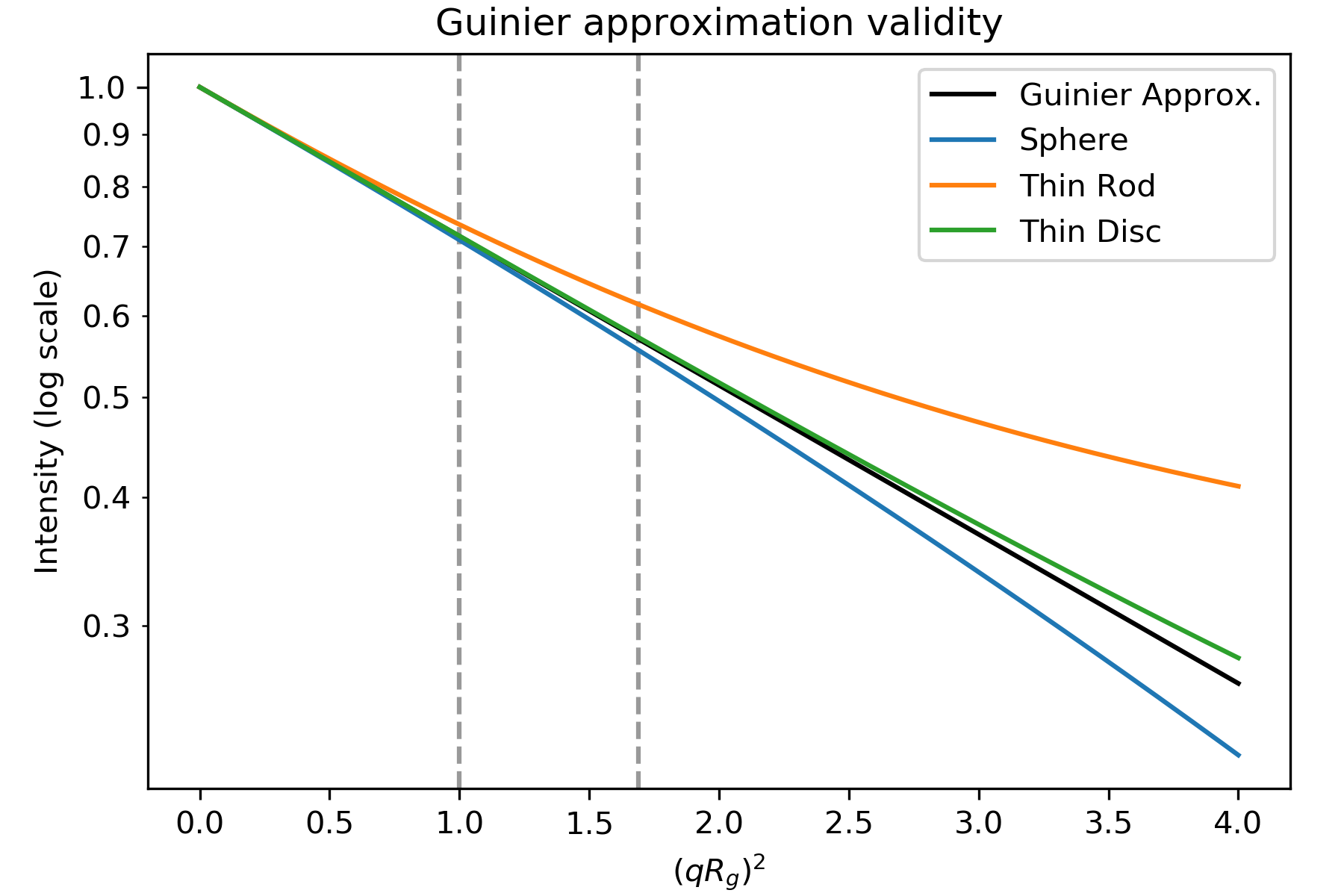
Kresba založená na obrázku 3.3 v . Intenzita pro geometrické tvary z tabulky 3.4 v . Čárkované čáry jsou při qRg 1,0 a 1,3((qRg) 2 1,0 a 1,69).
Jak vidíte, intenzita rozptylu pro tyč souhlasí s Guinierovou aproximací pouze do \(qR_g\sim 1,0\), pro kouli do \(qR_g\sim 1,3\) a pro disk do \(qR_g\sim 1,7\). V závislosti na celkovém tvaru částic byste tedy měli přizpůsobit různá množství dat s nízkým q, abyste získali dobrou Guinierovu shodu. (Poznámka:osa x grafu je (qRg) 2, takže \(qR_g\sim 1,3\) se objevuje jako přerušovaná čára na 1,69)
V praxi jsme fitovali kulovité (kulovité a diskovité) objekty až do \(qR_g\sim 1,3\), zatímco vysoce protáhlé (tyčinkovité) objekty jsme fitovali do \(qR_g\sim 1,0\). Tyto hodnoty byly zvoleny s <10% chybou vyplývající z odchylky skutečného tvaru od Guinierovy aproximace.Důvodem, proč akceptujeme tak velkou odchylku, je to, že nejistotu získáte také tím, že fitujete menší počet bodů ve vašich datech, takže existuje kompromis mezi tím, jak dobře funguje aproximace (fitování na menší maximální qRg) a jak dobře můžete fitovat vaše data (fitování na větší maximální qRg).
Rozsah Guinierova fitování je tedy v ideálním případě od nejstarší dostupné hodnoty q až do maximální hodnoty qRg 1,0 nebo 1,3. Nicméně vzhledem k tomu, že Rg je odvozenod Guinierova fitování, jak určíte správnou maximální hodnotu q pro konec fitování? Odpověď zní, že Guinierovo fitování se provádí iteračně:
- Odhadněte počáteční maximální hodnotu q pro fitování.
- Vypočítejte Guinierovo fitování a získejte Rg.
- Pokud qmaxRg > 1,3 (nebo 1,0), snižte maximální q. PokudqmaxRg < 1,3 (nebo 1,0), zvyšte maximální q.
- Pak opakujte kroky 2 a 3, dokud neskonvergujete ke konečnému maximálnímu q.
Většina softwaru v dnešní době provede toto iterační hledání za vás a u kvalitních dat vám poskytne rozumnou maximální hodnotu q, kterou možná bude třeba jen trochu ručně upřesnit.
Minimální hodnota q Guinierova fitování je obvykle určena minimální dostupnou hodnotouq ve vašich datech, která je nastavena přístrojem, na kterém měření provádíte. je však důležité mít dostatečně malé minimální q, abyste měli rozumný rozsah pro Guinierovo fitování. Obvykle by minimální hodnota qRg měla být\(qR_g\leq 0,65\), ačkoli u kulových systémů může být v pořádku\(qR_g\leq 1,0\). To znamená, že minimální požadovaná hodnota q závisí na velikosti měřeného systému. V některých případech, u zvláště velkých systémů, budete možná muset záměrně hledat přístroj, který může měřit na dostatečně nízké q.
Pokud mají vaše data problémy s kvalitou při nízkém q, což může být způsobeno výše uvedenými problémy, můžete zjistit, že vyloučení těchto dat z fitování může zlepšit kvalitu fitování. Ačkoli to může být přijatelné, měli byste při tom postupovat opatrně a na grafech vždy zobrazit celý rozsah dat.Nejpřijatelnějším případem je, když je prvních několik bodů příliš vysokých nebo příliš nízkých, ale zbytek rozsahu sedí dokonale (viz níže kritéria pro dobrý fit). V takovém případě může mít těch pár bodů, které jsou nejblíže k zarážce paprsku, špatnou statistiku nebo vyšší rozptyl instrumentálního pozadí a obvykle je lze bezpečně ignorovat.
.