Náhodné události, které se odehrávají ve spojitém prostoru vzorků, mohou vyvolat geometrické představy přinejmenším ze dvou důvodů: kvůli povaze problému nebo kvůli povaze řešení.

Některé problémy, jako Buffonova jehla, Ptáci na drátě, Bertrandův paradox nebo problém tyče rozlomené na tři kusy, vznikají ze své podstaty v geometrickém prostředí. Posledně jmenovaný problém také připouští vícenásobné přeformulování, které vyžaduje porovnání ploch geometrických útvarů. Obecně si můžeme geometrické pravděpodobnosti představit jako nezáporné veličiny (nepřesahující 1), které se přiřazují podoblastem daného oboru podle určitých pravidel. Je-li funkce μ vyjádřením tohoto přiřazení definovaným na doméně D, pak například požadujeme

0 ≤ μ(A) ≤ 1, A ⊂ D a
μ(D) = 1

Funkce μ obvykle není definována pro všechny A ⊂ D. Ty podmnožiny D, pro které je μ definována, jsou náhodné události, které tvoří určité výběrové prostory. Velmi často se μ definuje pomocí poměru ploch, takže je-li σ(A) definováno jako „plocha“ množiny A, pak lze stanovit μ(A) = σ(A) / σ(D).

Problém 1

Dva přátelé, kteří jezdí metrem do zaměstnání ze stejné stanice, přijíždějí do stanice rovnoměrně náhodně mezi 7. a 7:20 ráno. Jsou ochotni na sebe navzájem čekat 5 minut, poté nastoupí do vlaku, ať už společně, nebo sami. Jaká je pravděpodobnost jejich setkání ve stanici?“

V kartézském systému souřadnic (s, t) představuje čtverec o straně 20 (minut) všechny možnosti ranních příchodů obou přátel do stanice metra.

Šedá plocha A je ohraničena dvěma přímkami, t = s + 5 a t = s – 5, takže uvnitř plochy A platí, že |s – t| ≤ 5.

Dva kamarádi se setkají v metru. Z toho vyplývá, že dva kamarádi se setkají pouze za předpokladu, že jejich příchody s a t spadají do oblasti A. Pravděpodobnost, že se tak stane, je dána poměrem plochy A k ploše čtverce:

/ 400 = 175/400 = 7/16.

Problém 2

(.)

Na kružnici o poloměru 1 jsou náhodně umístěny tři body A, B, C. Na kružnici o poloměru 1 jsou umístěny tři body A, B, C, které se nacházejí v oblasti A. Jaká je pravděpodobnost, že ΔABC bude ostrý?“

Postavte bod C. Polohy bodů A a B jsou pak určeny oblouky α a β vycházejícími z bodu C ve dvou směrech. A priori víme, že 0 < α + β < 2π. Příznivé pro náš problém jsou hodnoty α a β (jako pod úhly ostré splňují) 0 < α < π a 0 < β < π. Jejich součet nemůže být menší než π, protože by tím vznikl úhel C tupý, proto platí α + β > π. Situace je znázorněna na následujícím obrázku, kde čtverec má stranu 2π.

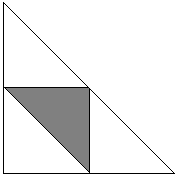
Region D je průsečíkem tří polopřímek: 0 < α, 0 < β a α + β < 2π. To je velký trojúhelník ve výše uvedeném diagramu. Příznivé události patří do stínovaného trojúhelníku, který je průsečíkem polorovin α < π, β < π a α + β > π. Poměr jejich ploch je zřejmě 1/4. V tomto trojúhelníku se nacházejí dvě roviny.

Nyní si všimněte, že pokud není náhodný trojúhelník ostrý, lze jej považovat za tupý, protože pravděpodobnost, že dva ze tří bodů A, B, C budou tvořit průměr, je 0. (Aby byl BC průměrem, měli bychom mít α + β = π, což je přímka, s nulou jako jediným možným přiřazením plochy). Můžeme tedy říci, že pravděpodobnost, že ΔABC je tupý, je 3/4. V případě tupého trojúhelníku lze kružnici rozdělit na dvě poloviny, přičemž trojúhelník leží celý v jedné z nich. Z toho vyplývá, že 3/4 je odpovědí na následující otázku:

Tři body A, B, C jsou náhodně umístěny na kružnici o poloměru 1. Na kružnici o poloměru 1 jsou umístěny tři body. Jaká je pravděpodobnost, že všechny tři leží v půlkruhu?“

1. E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Pět set matematických úloh podle (MAA, 1995, problém 244.)
2. D. A. Klain, G.-C. Rota Introduction to Geometric Probability , Cambridge University Press, 1997
3. A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions, Dover, 1978
4. A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Geometric Probability

• Geometric Probabilities
• Are Most Triangles Obtuse?
  • Osm výběrů v šesti sektorech
  • Tři náhodné body na kružnici
• Geometrická pravděpodobnost
  • Hůl rozdělená na tři části (trojúhelníkové souřadnice)
  • Hůl rozdělená na tři části. Řešení v kartézských souřadnicích
• Bertrandův paradox
• Ptáci na drátě (úloha a interaktivní simulace)
  • Ptáci na drátě: Řešení: Nathan Bowler
  • Ptáci na drátě. Solution by Mark Huber
  • Ptáci na drátě: pravděpodobnostní simulace. Řešení: Moshe Eliner
  • Ptáci na drátě. Řešení: Stuart Anderson
  • Birds on a Wire. Řešení: Bogdan Lataianu
• Simulace nudlí Buffona
• Průměrování dešťových kapek – cvičení z geometrické pravděpodobnosti
  • Průměrování dešťových kapek, část 2
• Obdélník na šachovnici: Úvod
• Označování a lámání tyčí
• Náhodné body na úsečce
• Pokrytí polokruhu
• Pokrytí polokoule
• Překrývající se náhodné intervaly
• Náhodné intervaly s jednou dominantou
• Body na čtvercové síti
• Ploché pravděpodobnosti na kouli
• Pravděpodobnost v trojúhelníku

|Kontakt|||Přední strana|||Obsah||Nahoře|

Copyright © 1996-2018 Alexander Bogomolny