Definice statistiky >Friedmanův test
Co je Friedmanův test?
Friedmanův test je neparametrický test pro zjišťování rozdílů v ošetřeních při více pokusech. Neparametrický znamená, že test nepředpokládá, že vaše data pocházejí z určitého rozdělení (například normálního rozdělení). V podstatě se používá místo testu ANOVA, když neznáte rozdělení svých dat.
Friedmanův test je rozšířením znaménkového testu, který se používá, když existuje více ošetření. Ve skutečnosti, pokud existují pouze dvě ošetření, jsou oba testy identické.
Provedení testu
Vaše data by měla splňovat následující požadavky:
- Data by měla být ordinální (např. Likertova škála) nebo spojitá,
- Data pocházejí z jedné skupiny, která byla měřena alespoň při třech různých příležitostech,
- výběr byl vytvořen metodou náhodného výběru,
- Bloky jsou vzájemně nezávislé (tj.tj. všechny dvojice jsou nezávislé – jedna neovlivňuje druhou),
- Pozorování jsou v rámci bloků seřazena bez vazeb.
Nulovou hypotézou pro test je, že všechna ošetření mají stejné účinky, nebo že se vzorky nějakým způsobem liší. Například mají různé středy, rozpětí nebo tvary. Alternativní hypotéza je, že ošetření mají různé účinky.
Připravte si data pro test.
Krok 1: Seřaďte data do bloků (sloupců v tabulce). pro tento příklad máme 12 pacientů, kteří dostávají tři různé léčby.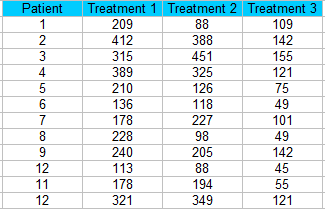
Krok 2: Seřaďte každý sloupec zvlášť. Nejmenší skóre by mělo získat pořadí 1. Řadím zde napříč řádky, takže každý pacient má pro každou léčbu pořadí 1, 2 nebo 3.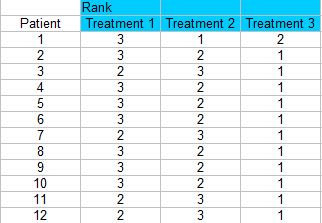
Krok 3: Sečtěte pořadí (zjistěte součet pro každý sloupec).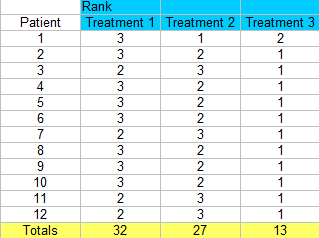
Provedení testu
Poznámka: Tento test se obvykle neprovádí ručně, protože výpočty jsou časově a pracovně náročné. Téměř všechny populární statistické softwarové balíky umí tento test spustit. Přesto zde pro informaci uvádím ruční postup.
Krok 4: Vypočítejte testovací statistiku. Budete potřebovat:
- n: počet subjektů (12)
- k: počet ošetření (3)
- R: celkové pořadí pro každý ze tří sloupců (32, 27, 13).
Vložte je do následujícího vzorce a vyřešte: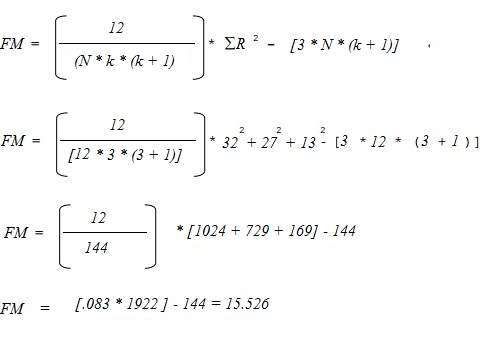
Krok 5: Najděte kritickou hodnotu FM z tabulky kritických hodnot pro Friedmana (viz tabulka níže).
Použijte tabulku k=3 (protože tolik máme ošetření) a hladinu alfa 5 %. Můžete zvolit vyšší nebo nižší hladinu alfa, ale 5 % je poměrně běžná hodnota – pokud tedy neznáte svou hladinu alfa, použijte tabulku 5 %.
Podíváme-li se na n-12 v této tabulce, zjistíme, že kritická hodnota FM je 6,17.
Krok 6: Porovnejte vypočtenou testovací statistiku FM (krok 4) s kritickou hodnotou FM (krok 5). Pokud je vypočtená hodnota F větší než kritická hodnota FM, nulovou hypotézu zamítněte:
- Vypočtená testová statistika FM = 15,526.
- Kritická hodnota FM z tabulky = 6,17.
Vypočtená statistika FM je větší, takže byste zamítli nulovou hypotézu.
Tabulka kritických hodnot Friedmanovy ANOVY podle řad
Tři tabulky podle „k“.
Pokud je vaše k větší než 5 nebo vaše n větší než 13, použijte tabulku kritických hodnot chí kvadrátu v kroku 5, abyste získali kritickou hodnotu.
k=3
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 6.00 | 6.00 | – |
| 4 | 6.00 | 6.50 | 8.00 |
| 5 | 5.20 | 6.40 | 8.40 |
| 6 | 5.33 | 7.00 | 9.00 |
| 7 | 5.43 | 7.14 | 8.86 |
| 8 | 5.25 | 6.25 | 9.00 |
| 9 | 5.56 | 6.22 | 8.67 |
| 10 | 5.00 | 6.20 | 9.60 |
| 11 | 4.91 | 6.54 | 8.91 |
| 12 | 5.17 | 6.17 | 8.67 |
| 13 | 4.77 | 6,00 | 9,39 |
| ∞ | 4,61 | 5,99 | 9,21 |
k=4
| α <.10 | α ≤.05 | α <.01 | |
| 2 | 6.00 | 6.00 | – |
| 3 | 6.60 | 7.40 | 8.60 |
| 4 | 6.30 | 7.80 | 9.60 |
| 5 | 6.36 | 7.80 | 9.96 |
| 6 | 6.40 | 7.60 | 10.00 |
| 7 | 6.26 | 7.80 | 10.37 |
| 8 | 6.30 | 7.50 | 10.35 |
| ∞ | 6.25 | 7.82 | 11.34 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 7.47 | 8.53 | 10.13 | 4 | 7.60 | 8.80 | 11.00 | 5 | 7.68 | 8.96 | 11.52 | ∞ | 7.78 | 9.49 | 13,28 |
Odkaz:
Friedmanova dvoucestná analýza rozptylu podle řad – analýza dat k-skupin s
kvantitativní proměnnou odpovědi. Získáno 7-17-2016 z: http://psych.unl.edu/psycrs/handcomp/hcfried.PDF
Stephanie Glen. „Friedmanův test / dvoucestná analýza rozptylu podle řad“ From StatisticsHowTo.com: Základní statistika pro nás ostatní! https://www.statisticshowto.com/friedmans-test/
——————————————————————————
Potřebujete pomoci s domácím úkolem nebo testovou otázkou? S Chegg Study můžete získat řešení svých otázek krok za krokem od odborníka v oboru. Prvních 30 minut s lektorem Chegg je zdarma!