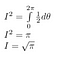Lord Kelvin o tomto integrálu napsal: „
Užijte si to 😉
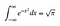
OK, takže budu předpokládat, že znáte základy integrování a diferencování. Následující text přidá trochu intuice k chytrým trikům, které přijdou na řadu později. Nebojte se, pokud vás něco z toho lehce zmate, jen se snažte získat cit pro to, co se děje.
Strategie zde bude spočívat v chytré substituci. Budeme však provádět substituci ve dvou proměnných. Současný problém si můžete představit jako výpočet plochy pod křivkou
Ukážeme si však, že problém lze změnit na výpočet objemu.
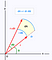
Pro výpočet objemu použijeme trochu jiný vzorec pro změnu proměnné, než jaký se používá v běžných integrálech. Budeme používat polární souřadnice. Tím vyjádříme souřadnice x a y v podobě jejich poloměru a úhlu. Geogebra má pěkný interaktivní způsob, jak to zobrazit zde

Poté použijeme kouzelný vzorec pro změnu základny polárních souřadnic.
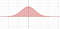
Při výpočtu plochy pod křivkou jsme měli prvek ‚dx‘, který představuje malou vzdálenost podél osy x. Při výpočtu plochy pod křivkou jsme měli prvek ‚dx‘, který představuje malou vzdálenost podél osy x. Při výpočtu objemu máme dx dy, což je jako malý obdélník o délce strany dx a dy. Z těchto základen pak vytvoříme řadu políček, která odhadují objem. Nejsnáze je to vidět na níže uvedené vizualizaci. Integrál je limitou těchto aproximací.
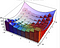
Když místo toho použijeme polární souřadný systém, máme pod sebou trochu jiný plošný prvek. Níže se nachází plošný prvek dA. Při malých změnách úhlu a poloměru lze tento plošný prvek stále lépe aproximovat obdélníkem o délkách stran dr, resp. r*dtheta. Pokud se trochu vyznáte v geometrii, pro malá theta se sin(theta) velmi dobře aproximuje pomocí theta a vy pak můžete dokázat níže uvedený výsledek.
Řešení integrálu
Nejprve pojmenujeme náš integrál. Nazveme ho I.
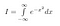
Všimněte si, že x je pouze „fiktivní proměnná“. Oblast existuje bez ohledu na to, jaký název proměnné použijeme. Můžeme tedy napsat i následující dvě rovnice
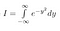
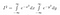
Nyní, protože I je jen konstanta, i když její hodnotu ještě neznáme, můžeme použít naše běžná pravidla pro uvádění konstanty uvnitř integrálu
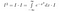
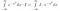
Dosud jsme toho moc podstatného neudělali. Nyní se důkladně zamyslíme nad tím, co znamená integrál. Vezmeme si integrály funkcí. Pokud dvě funkce nabývají všude stejných hodnot, jsou stejné a mají stejnou plochu. S tímto vědomím můžeme provádět následující manipulace, pokud se na I*exp(-x²) díváme jako na funkci x, tj. na něco, co přijímá hodnoty x jako vstup a dává číslo jako výstup.
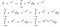
Ok, to bylo hodně náročné. V prvním řádku jsme jen přepsali I v jeho integrálním tvaru s jiným názvem proměnné. Ve druhém řádku, kde jsme považovali I*exp(-x²) za funkci, jsme si uvědomili, že můžeme exp(-x²) přenést dovnitř integrálu dy, a tím bychom získali stále stejnou výstupní hodnotu pro libovolnou vstupní hodnotu x. Nakonec jsme použili pravidla pro exponenciování.
Přepíšeme-li to celé, máme nyní
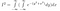
Následuje vražedný poznatek. Výše jsme si pohráli s názvy proměnných a se způsobem reprezentace funkce. Nyní změníme pohled: tento výraz představuje také integrál exp(-(y²+x²)) po celé 2D rovině, přičemž prvek plochy dA = dx dy. Tj. dx dy je malý obdélník v rovině a exp(-(y²+x²)) je výška nad tímto obdélníkem.
Dále použijeme poznatky o polárních souřadnicích z dřívějška
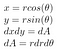
Jako sin² + cos² = 1, po zapojení všeho, dostaneme
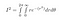
r v rozsahu od 0 do nekonečna a theta v rozsahu od 0 do 2*pi, protože to pokrývá celou 2D rovinu: libovolný bod má poloměr menší než nekonečno a úhel mezi 0 a 2pi radiánů.
Vnitřní integrál můžeme vyhodnotit pomocí řetězového pravidla
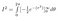
A do země zaslíbené jsme se nyní dostali: