Kolik toho víte o nekonečnu? Pravděpodobně jste už slyšeli o čísle, které je největší možné nebo nemožně velké.
Abych mohl vysvětlit nekonečno, musím nejprve definovat některé pojmy.
Nekonečna jsou čísla, která se používají k počítání. Množina celých čísel je definována jako všechna čísla bez zlomkových složek. Některé příklady jsou následující: -12, 0, 1, 3, 42, 17.
Nekonečno je pojem objektu mimo dosah přirozených čísel. Poprvé jej konceptualizoval ruský matematik Georg Cantor, který nejen zavedl nekonečno, ale také odhalil, že existuje více nekonečen.
Cantor podal kontroverzní důkaz nekonečna, který říká, že některá nekonečna jsou větší než jiná. Na první pohled se to může zdát nemožné – jak může být objekt větší než jiný objekt, který je nekonečný?“

Cantor svůj důkaz založil na zdánlivě zbytečném odvětví matematiky: Teorie množin. Množina je soubor objektů – například můžeme mít množinu, která obsahuje 1, 2 a 3. V tomto případě se jedná o soubor objektů. Tyto objekty v množině se nazývají prvky.
V matematickém zápisu by to vypadalo takto:
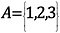
Počet prvků v této množině, neboli kardinalita množiny, je 3.
Tato množina se označuje jako:
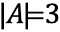
Máme-li nyní další množinu B, obsahující objekty, takové, že
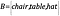
Jak poznáme, že množiny mají stejnou velikost?
Jedním ze způsobů, jak to můžeme zjistit, je spočítat počet prvků druhé množiny. Jasně vidíme, že i tato množina má 3 prvky, a tak víme, že mají stejnou velikost.
Dalším způsobem, jak to můžeme zjistit, je porovnat naši druhou množinu B s první množinou A pomocí mapování.
První prvek z množiny A , 1, můžeme namapovat na první prvek množiny B, křeslo.
Druhý prvek z množiny A, 2, můžeme mapovat na druhý prvek množiny B, stůl.
Třetí prvek z množiny A, 3, můžeme mapovat na třetí prvek množiny B, klobouk.
Protože každý prvek z A je mapován na přesně 1 prvek z B, mají množiny stejnou velikost.
Podívejme se nyní na nekonečné množiny. Množina celých čísel, kterou jsme zmínili na začátku, je nekonečná množina – existuje nekonečný počet celých čísel. Množinu celých čísel označujeme symbolem
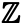
Množina sudých čísel, kterou můžeme označit jako

je definována jako
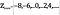
Intuitivně, se může zdát, že
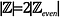
jako na každé sudé celé číslo připadají 2 celá čísla: 1 liché celé číslo a 1 sudé celé číslo. Ověřme si to.
Zkusme porovnat množiny mapováním prvků z 1 množiny do druhé.
Můžeme mapovat 1 na 2, 2 na 4, 3 na 6 atd.
Pokračujeme-li tímto způsobem po celých množinách, vidíme, že každý prvek z celočíselné množiny se mapuje na přesně 1 prvek ze sudé celočíselné množiny.
Takto, ač se to může zdát protiintuitivní, jsou velikosti množin stejné.
Přestože se to může zdát protiintuitivní, jsou velikosti množin stejné.