Cuando la luz se refleja o transmite desde una estructura material se produce un cambio de polarización. La elipsometría mide esta respuesta que depende de las propiedades ópticas y del grosor de cada material. La elipsometría se utiliza principalmente para determinar las constantes ópticas y el espesor de la película, pero también para caracterizar la composición, la cristalinidad, la rugosidad, la concentración de dopaje y otras propiedades del material asociadas a un cambio en la respuesta óptica.

Las áreas de aplicación son la investigación básica en ciencias físicas, las soluciones de almacenamiento de datos y semiconductores, las pantallas planas, la comunicación, los biosensores y las industrias de revestimiento óptico. La elipsometría también tiene la flexibilidad de medir la mayoría de los tipos de materiales: dieléctricos, semiconductores, metales, superconductores, orgánicos, revestimientos biológicos y compuestos.

Definición de luz polarizada

La luz puede describirse como una onda electromagnética que viaja por el espacio. La forma en que se comporta el campo de una onda electromagnética en relación con el espacio y el tiempo se denomina polarización. Se considera que la luz no está polarizada cuando su orientación y fase son totalmente arbitrarias. La elipsometría, sin embargo, mide la luz polarizada, es decir, un campo eléctrico que sigue una trayectoria específica y tiene una forma distinta en un punto determinado. Una onda electromagnética que viaja en la dirección z puede describirse por sus componentes x e y, porque su campo eléctrico es siempre ortogonal a la dirección de propagación. Cuando dos ondas luminosas ortogonales están en fase, la luz resultante está linealmente polarizada. Su orientación está determinada por las amplitudes relativas. La luz se considera circularmente polarizada si las ondas ortogonales están desfasadas 90° y tienen la misma amplitud. La polarización más común es la elíptica y combina ondas ortogonales de amplitud y fase arbitrarias. De ahí que la elipsometría reciba su nombre.

Diferentes tipos de polarización:

Lineal

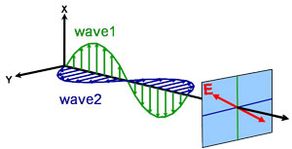
Circular

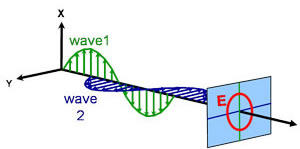
Elíptica

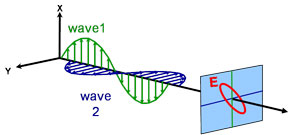
Propiedades ópticas

Las propiedades ópticas que determinan cómo interactúa la luz con un material se describen mediante dos valores. Generalmente se representan como un número complejo. El índice de refracción complejo (ñ) está formado por el índice (n) y un coeficiente de extinción (k):

Las propiedades ópticas también pueden representarse como una función dieléctrica compleja:

con la siguiente relación entre convenciones:

El índice representa la velocidad de fase de la luz cuando viaja en un material en comparación con la velocidad de la luz cuando viaja en el vacío, c:

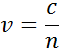
Al entrar en un material con un índice más alto, la luz se ralentiza. Como la frecuencia de las ondas de luz no cambia, la longitud de onda se acorta. La pérdida de energía de las ondas en el material se describe mediante el coeficiente de extinción, que está relacionado con el coeficiente de absorción de la siguiente manera:

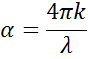
De acuerdo con la Ley de Beer, la luz pierde intensidad en un material absorbente. El coeficiente de extinción demuestra la rapidez con la que la luz desaparece en un material.

La figura 4 muestra una onda de luz que viaja a través de dos materiales diferentes de distintas propiedades antes de volver al ambiente.

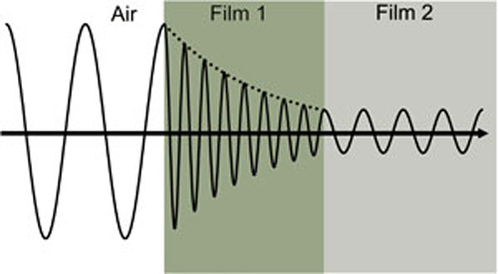
Figura 4: Onda de luz que viaja desde el aire a la película absorbente 1 y luego a la película transparente 2. La velocidad de fase y la longitud de onda cambian en ambos materiales en función del índice de refracción (Película 1: n=4, Película 2: n=2).

La longitud de onda determina las constantes ópticas. La figura 5 muestra las constantes ópticas del TiO2 desde el UV hasta el IR. Debido a los diferentes procesos que extraen energía de la onda luminosa, la absorción (k>0) se produce tanto en el UV como en el IR. La absorción en el IR suele estar causada por la vibración molecular o de los fonones o por los portadores libres. La absorción en el UV suele producirse por transiciones electrónicas, en las que la energía de la luz excita a los electrones a estados elevados. La figura 5 muestra que las constantes ópticas hipotéticas o reales no son independientes, sino que están vinculadas matemáticamente a través de las relaciones de Kramers-Kronig.

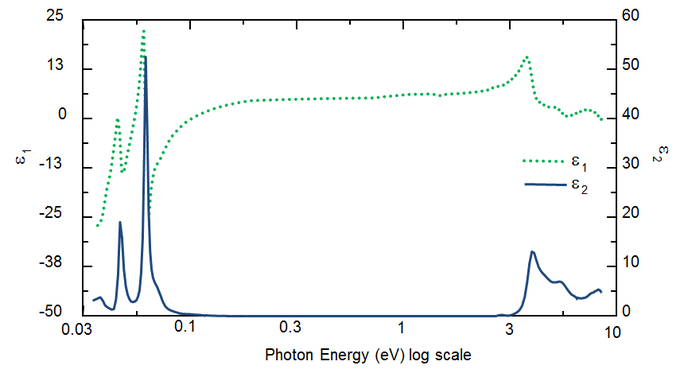
Figura 5: Función dieléctrica compleja para una película de TiO2 con longitudes de onda desde el IR (pequeños eV) hasta el UV (altos eV).

Interacción de la luz y los materiales

Siempre que la luz interactúa con un material se producen condiciones de contorno en la interfaz. Durante esto, las ecuaciones de Maxwell deben permanecer siempre satisfechas. La siguiente figura muestra cómo la luz incidente se refleja y refracta en la interfaz. El ángulo entre el rayo incidente y la normal de la muestra (θi) será igual al ángulo reflejado (θr). La luz que entra en un material se refracta con un ángulo θt dado por:

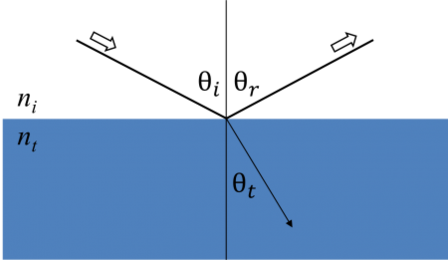
Figura 6: La luz se refleja y refracta según la ley de Snell.

En toda interfaz una parte de la luz se refleja mientras que el resto se transmite en el ángulo refractado. Dependiendo de las condiciones de contorno, se aplican diferentes soluciones para los campos eléctricos paralelos y perpendiculares a la superficie de la muestra. Así, la luz puede separarse en componentes ortogonales con respecto al plano de incidencia (polarización p y s). Ambas componentes pueden calcularse por separado. Así es como Fresnel describió la cantidad de luz reflejada y transmitida en una interfaz entre materiales:

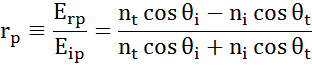
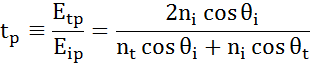
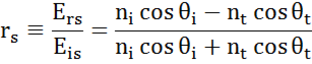
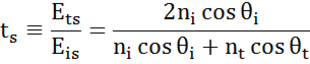
Las interfaces múltiples con coeficientes de reflexión y transmisión de Fresnel adecuados se producen con estructuras de película fina y multicapa. Para definir correctamente el haz reflejado o transmitido, es necesario seguir la fase relativa de cada componente de la luz. Así, el espesor de la fase de la película se determina de la siguiente manera:

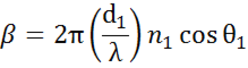
Cuando se superponen varias ondas luminosas, se produce una interferencia que depende de la fase relativa de cada onda luminosa individual. La siguiente figura muestra la combinación de ondas luminosas en el haz reflejado y sus correspondientes cálculos de Fresnel.

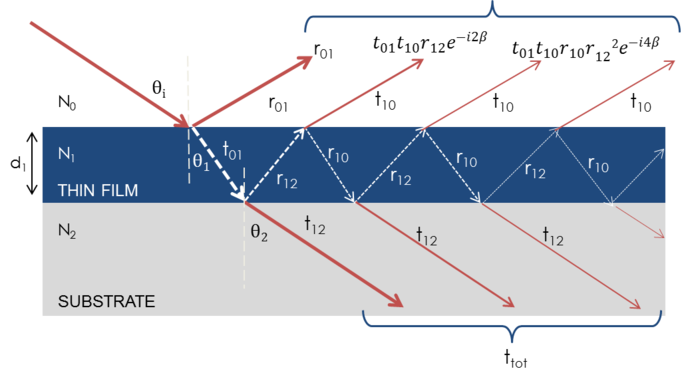
Figura 7: La luz se refleja y refracta en cada interfaz individual, lo que da lugar a múltiples haces en una película fina. La interferencia de los haces depende de la fase y la amplitud relativas de los campos eléctricos. La reacción del haz puede calcularse con los coeficientes de reflexión y transmisión de Fresnel.

Mediciones

La elipsometría mide principalmente cómo reaccionan los componentes p y s entre sí durante la reflexión o la transmisión. Por tanto, un haz de referencia siempre forma parte del experimento. Se refleja o transmite una polarización conocida desde la muestra y se mide la polarización de salida. El cambio de polarización es la medida de elipsometría:

La figura 6 muestra una típica medida de elipsometría de la muestra. La luz lineal incidente tiene componentes p- y s-. La luz reflejada muestra cambios de amplitud y fase para la luz polarizada p- y s-. Estos cambios se miden por ellipsometría.

Para recoger datos de ellipsometría se necesita lo siguiente: fuente de luz, generador de polarización, muestra, analizador de polarización y detector. Tanto el generador de polarización como el analizador están formados por piezas ópticas que manipulan la polarización: compensadores, polarizadores y moduladores de fase. Las configuraciones típicas de los elipsómetros incorporan un analizador giratorio (RAE), un polarizador giratorio (RPE), un compensador giratorio (RCE) y una modulación de fase (PME). La figura siguiente muestra una configuración RAE.

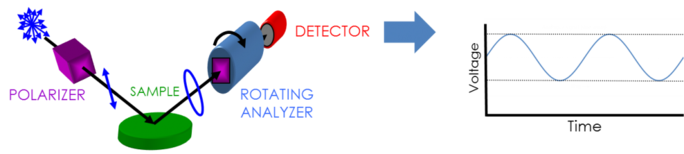
La luz no polarizada es producida por una fuente de luz y luego enviada a través de un polarizador. El polarizador se ajusta para permitir que sólo pase la luz con una determinada orientación del campo eléctrico. Como el eje del polarizador está alineado entre los planos p y s, ambos llegan a la superficie de la muestra. La luz, ahora polarizada linealmente, se refleja en la superficie de la muestra, convirtiéndose en polarizada elípticamente, y luego se envía a través de un polarizador de rotación continua (el «analizador»). La cantidad de luz que se deja pasar depende de la orientación del polarizador en relación con la elipse del campo eléctrico de la muestra. Para definir la polarización reflejada, la luz se convierte en una señal electrónica en el detector. La comparación de estos datos con la polarización de entrada establecida proporciona información sobre el cambio causado por la reflexión de la muestra: la medición elipsométrica de Psi y Delta.

Análisis de datos

La elipsometría se utiliza para definir el grosor de la película del material o las constantes ópticas midiendo los cambios en la polarización de la luz. Las «pseudo» constantes ópticas de la medición de elipsometría pueden derivarse invirtiendo los datos determinados para una sola reflexión. Esto es útil para el material a granel.

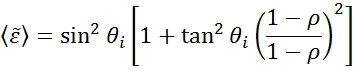
La ecuación anterior no cuenta con ninguna capa superficial. Sin embargo, normalmente hay un óxido o rugosidad superficial en los materiales a granel. Una inversión directa incluirá estos datos como parte de las constantes ópticas a granel. Véase en la fig. 10 un resumen de un proceso típico de análisis de datos utilizado en las mediciones de elipsometría. Como no se puede escribir una ecuación exacta, es necesario un análisis de regresión. La respuesta suele estar sobredeterminada con sólo unas pocas incógnitas y cientos de puntos de datos experimentales. Un análisis de regresión permite incluir todos los datos medidos a la hora de determinar la solución.

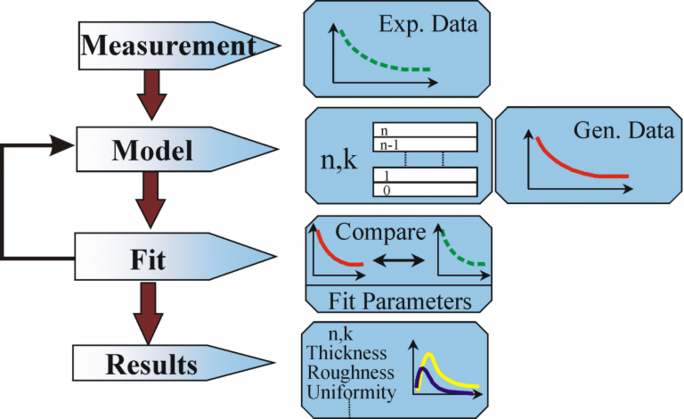
Figura 10: Diagrama de flujo para el análisis de datos de elipsometría.

El siguiente procedimiento se utiliza para el análisis de datos: se mide la muestra y se hace un modelo de la misma. Con ayuda de este modelo se calculan los resultados supuestos de las ecuaciones de Fresnel, que describen el espesor y las constantes ópticas de cada material. Se realiza una evaluación del cálculo preliminar, si estos valores son desconocidos. Los valores calculados se comparan con los datos experimentales. Para que los datos experimentales y de cálculo coincidan mejor, se pueden variar los datos desconocidos del material. Sin embargo, los puntos de datos experimentales deben ser siempre más que los parámetros desconocidos. Por ejemplo, como máximo se pueden determinar dos propiedades del material con un elipsómetro de una sola longitud de onda, ya que produce exactamente dos puntos de datos: Ψ, Δ (Psi y Delta). La regresión se utiliza para encontrar la mejor coincidencia entre el modelo y el experimento. La diferencia entre las curvas de datos se cuantifica con ayuda de un estimador como el Error Medio Cuadrado (MSE). Las propiedades desconocidas se varían hasta que se alcanza el MSE mínimo. Esto significa que el MSE más bajo equivale a la mejor respuesta.

Vea en la figura siguiente la curva MSE frente al espesor de la película para una película transparente sobre silicio. El valor más bajo de MSE se produce en un espesor de 749 nm a pesar de una serie de mínimos locales. Por lo tanto, el espesor correcto de la película es también de 749 nm. El algoritmo de regresión puede considerar que un mínimo local es correcto. Por lo tanto, para determinar el mínimo global correcto es prudente comparar los resultados a ojo para el MSE más bajo.

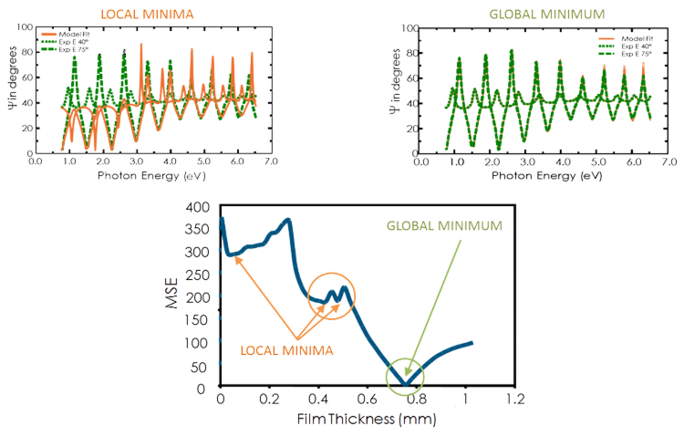
Figura 11, arriba a la derecha: Datos experimentales y curvas correspondientes generadas para el modelo en el mínimo global. Figura 11, arriba-izquierda: Una curva similar en el mínimo local cerca de un espesor de 0,45 µm puede identificarse fácilmente como resultado incorrecto. Figura 11, abajo: La curva de MSE frente al grosor muestra el mínimo global. Un algoritmo de regresión puede dar los mínimos locales, pero no el resultado final.

Determinación del espesor de la película

El espesor de la película suele determinarse por la interferencia entre la luz que se refleja en la superficie y la que viaja a través de la película. Que esta interferencia se considere constructiva o destructiva depende de la fase relativa de la luz que se une a la reflexión de la superficie. La interferencia incluye tanto información de amplitud como de fase. La información de fase de Δ es muy sensible a las películas hasta el grosor de la subcapa. Véase en la siguiente figura una comparación de la intensidad reflejada y la elipsometría para la misma serie de capas finas de SiO2 sobre Si. La reflectancia para cada película es casi la misma mientras que hay grandes variaciones en Δ.

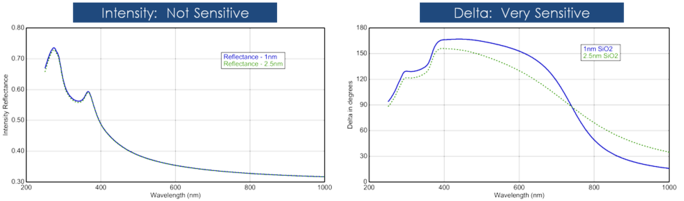
Figura 12, izquierda: Intensidad reflejada y delta elipsométrico (derecha) para dos óxidos delgados sobre silicio. La medición de la intensidad no muestra que Delta sea muy sensible a las películas de escala nanométrica.

La elipsometría se utiliza comúnmente para películas desde subnanómetros hasta unas pocas micras de espesor. Con películas de un grosor superior a varias decenas de micras, las oscilaciones de interferencia sólo pueden resolverse con creciente dificultad, excepto cuando se utilizan longitudes de onda infrarrojas más largas. Por ello, para las películas más gruesas se suelen utilizar otras técnicas de medición.

Para medir el espesor, una parte de la luz tiene que atravesar toda la película y volver a la superficie. En el caso de los materiales que absorben la luz, las mediciones ópticas de espesor sólo pueden realizarse en capas finas y semiopacas, a menos que se realicen en regiones espectrales con menor absorción. Por ejemplo, una película orgánica que absorbe la luz ultravioleta e infrarroja puede ser transparente en las longitudes de onda medias visibles. Los metales absorben fuertemente en todas las longitudes de onda, por lo que el espesor máximo de la capa que puede determinarse se sitúa en torno a los 100 nm.

Constantes ópticas

Las constantes ópticas desempeñan un papel importante en las mediciones de espesor. El espesor de una película influye en la longitud de la trayectoria de la luz que viaja a través de la película, el índice determina la velocidad de la onda de luz y el ángulo de refracción. Por lo tanto, ambos contribuyen al retraso entre la luz que viaja a través de la película y la reflexión en la superficie. Es necesario establecer n y k, así como el espesor, para obtener resultados correctos de una medición óptica.

Como las constantes ópticas de un material varían para diferentes longitudes de onda, todas las longitudes de onda que se analizan con el elipsómetro deben determinarse individualmente. La respuesta de un material en cada longitud de onda puede anticiparse utilizando una tabla de constantes ópticas. Para evitar el minucioso ajuste de las constantes ópticas desconocidas longitud de onda por longitud de onda es favorable utilizar todas las longitudes de onda simultáneamente. Los parámetros ajustables de una relación de dispersión, por ejemplo, permiten que la forma general de la constante óptica coincida con los resultados experimentales. En comparación con el ajuste de los valores individuales de n y k para cada longitud de onda, el número de parámetros libres desconocidos se reduce considerablemente.

Las relaciones de Cauchy o Sellmeier se utilizan con frecuencia para describir el índice de los materiales transparentes, donde la relación de Cauchy se da normalmente como:

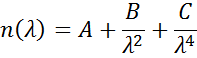
con los tres términos ajustados para que coincidan con el índice de refracción del material. La relación de Cauchy no está limitada por la consistencia de Kramers-Kronig (KK) y puede conducir a una dispersión no física. La relación de Sellmeier, por otro lado, impone la consistencia de Kramers-Kronig (KK), que asegura que la dispersión óptica mantiene una forma realista. La relación de Sellmeier suele escribirse como:

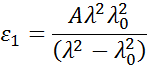
Los materiales absorbentes suelen tener una región de longitud de onda transparente que puede modelarse con la relación de Cauchy o de Sellmeier. Sin embargo, la región de absorción debe tener en cuenta las constantes ópticas reales e imaginarias. Para describir la absorción de varios materiales, muchas relaciones de dispersión utilizan la teoría del oscilador, incluyendo Lorentz, Harmonic y Gauss. Todas ellas comparten atributos similares con las características de absorción que se describen con la amplitud, el ensanchamiento y la energía central (relacionada con la frecuencia de la luz). La forma de la componente real se calcula utilizando la consistencia de Kramers-Kronig después de que el comportamiento imaginario sea descrito por el oscilador. Para incluir una posible absorción adicional más allá de la región espectral medida, se añade un desplazamiento a la componente real. El oscilador de Lorentz puede escribirse como:

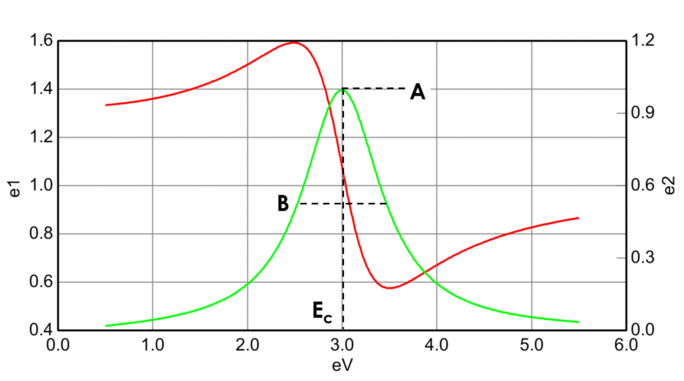
La figura 13 también muestra la amplitud (A), el ensanchamiento (B), la energía central (Ec) y el desplazamiento (e1, off set) para un oscilador de Lorentz típico. La energía E está relacionada con la frecuencia de una onda, n:

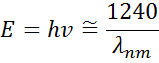
La constante de Planck h y la longitud de onda λ están dadas en nanómetros. Otros modelos de dispersión, como el de Tauc-Lorentz y el de Cody-Lorentz, incorporan términos para describir la energía de la banda prohibida.

Lectura adicional

La elipsometría es una técnica óptica establecida para la medición de películas delgadas y materiales a granel. Utiliza los cambios de polarización causados por la reflexión/transmisión de la estructura de un material para determinar sus características, como el espesor y las constantes ópticas.

Aspnes D.E. (1985). The Accurate Determination of Optical Properties by Ellipsometry. En: Palik E.D. (ed.) Handbook of Optical Constants of Solids, pp. 89-112. Academic Press, Orlando.

Azzam R.M.A. y Bashara N.M. (1987). Ellipsometry and Polarized Light, Elsevier Science B.V., Amsterdam, The Netherlands.

Boccara A.C., Pickering C., and Rivory J. (eds.), (1993). Spectroscopic Ellipsometry, Elsevier Publishing, Amsterdam.

Collins R.W., Aspnes D.E., y Irene E.A. (eds.), (1998). «Proceedings from the Second International Conference on Spectroscopic ellipsometry». En: Thin Solid Films, vols. 313-314.

Fujiwara H., Spectroscopic Ellipsometry, Principles and Applications, John Wiley & Sons, Ltd. 2007

Gottesfeld S., Kim Y.T., y Redondo A. (1995). «Recent applications of ellipsometry and spectroellipsometry in electrochemical systems», En: I. Rubinstein (ed.), Physical Electrochemistry: Principles, Methods, and Applications, Marcel Dekker, New York.

Herman, I.P. (1996). Optical Diagnostics for Thin Film Processing, pp 425-479. Academic Press, San Diego, California.

Johs B. et al (1999). «Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part II: Advanced Applications». Optical Metrology, vol. CR72, pp 29-58. SPIE, Bellingham, Washington.

Johs B. et al (2001). «Desarrollos recientes en elipsometría espectroscópica para aplicaciones in situ». In: Duparré A, Singh B (ed.) Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II, vol. 4449, pp 41-57. SPIE, Bellingham, Washington.

Roseler A. (1990). Infrared Spectroscopic Ellipsometry, Akademie-Verlag, Berlín.

Rossow U. y Richter W. (1996). «Ellipsometría espectroscópica» en: Bauer G y Richter W (eds.) Optical Characterization of Epitaxial Semiconductor Layers, pp. 68-128, Springer-Verlag, Berlín.

Tompkins H.G. (1993). A User’s Guide to Ellipsometry, Academic Press, San Diego, California.

Tompkins H.G. y McGahan W.A. (1999). Spectroscopic Ellipsometry and Reflectometry, John Wiley & Sons, Inc., USA.

Tompkins, H.G. e Irene E.A. (eds.), 2005, Handbook of Ellipsometry, William Andrew Publishing, New York.

Tompkins, H. G. y Hilfiker, J. H., Spectroscopic Ellipsometry, Practical Application to Thin Film Characterization, 2016, Momentum Press Engineering

Woollam J.A. y Snyder P.G. (1992). «Elipsometría espectroscópica de ángulo variable» en: Brundle CR, Evans CA, y Wilson S (eds) Encyclopedia of Materials Characterization: Surfaces, Interfaces, Thin Films, pp. 401-411, Butterworth-Heinemann, Boston.

Woollam J.A. et al (1999). «Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part I: Basic Theory and Typical Applications». Optical Metrology, vol. CR72, pp 3-28. SPIE, Bellingham, Washington.

Woollam J.A. (2000). «Ellipsometry, Variable Angle Spectroscopic» en: Webster J.G. (ed.) Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 109-116. John Wiley & Sons, New York.