Cómo calcular la tensión en las cuerdas que suspenden un objeto
Podemos ver en la ilustración de abajo que la fuerza, F, necesaria para levantar el objeto es igual al peso, W, del objeto. Esta idea es el concepto fundamental que subyace en nuestra fórmula de la fuerza de tensión. También se muestra a continuación el diagrama de cuerpo libre del objeto que muestra las fuerzas de tensión, T, que actúan en la cuerda. Como puedes ver, las fuerzas de tensión vienen en pares y en direcciones opuestas:
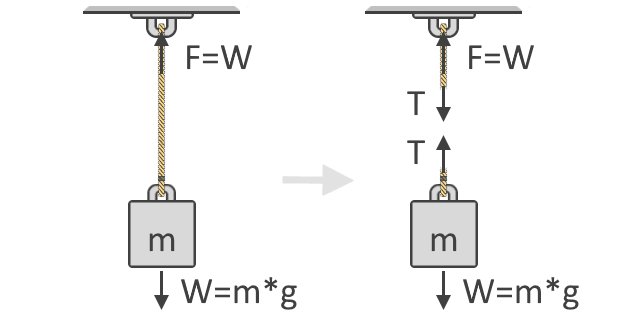
Siguiendo la Segunda Ley del Movimiento de Newton, podemos entonces expresar la suma de fuerzas usando el diagrama de cuerpo libre del objeto, como se muestra en el lado derecho de la ilustración anterior. Utilizamos los diagramas de cuerpo libre para mostrar las diferentes direcciones y magnitudes de las fuerzas que actúan sobre un cuerpo. En equilibrio, estas fuerzas deberían ser todas iguales a cero. Considerando todas las fuerzas hacia arriba como positivas y hacia abajo como negativas, nuestra ecuación es:
ΣF = 0 = T + (-W)T = W
donde el peso, W, se vuelve negativo ya que está dirigido hacia abajo. Transponiendo W al otro lado de la ecuación, podemos ver ahora que la fuerza de tensión en la cuerda es igual al peso del objeto que lleva, como también se muestra arriba.
Si usamos más cuerdas para levantar el objeto, la fuerza de tensión total se divide en las cuerdas. La fuerza de tensión en cada cuerda depende de sus ángulos con respecto a la dirección de la fuerza a la que se opone. Para entender mejor esto, consideremos otro diagrama de cuerpo libre de un objeto suspendido por dos cuerdas, como se muestra a continuación:
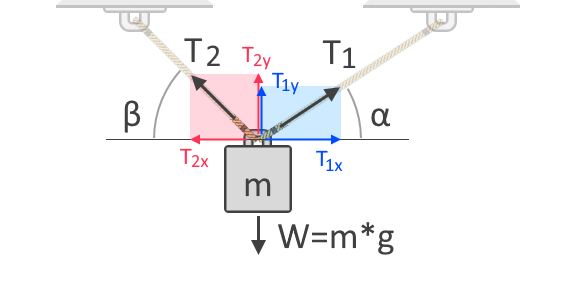
En el diagrama de cuerpo libre mostrado arriba, podemos ver las componentes horizontal y vertical de las fuerzas de tensión, T₁ y T₂. Las fuerzas son vectores, lo que significa que siempre tienen magnitudes y direcciones. Como todos los vectores, las fuerzas pueden expresarse en estas componentes que dan la influencia de la fuerza a lo largo de los ejes horizontal y vertical. T₁ₓ y T₂ₓ son las componentes verticales de T₁ y T₂, respectivamente. Por otro lado, T₁ᵧ y T₂ᵧ son las componentes verticales de las mismas fuerzas, respectivamente. Como la gravedad actúa sobre el objeto en el eje vertical, necesitamos considerar las componentes verticales de las fuerzas de tensión para nuestra suma de fuerzas como sigue:
ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)W = T₁ᵧ + T₂ᵧ
Como también conocemos los ángulos de las fuerzas de tensión, podemos expresar T₁ᵧ y T₂ᵧ en términos de T₁ y T₂, respectivamente, con la ayuda de funciones trigonométricas:
T₁ᵧ = T₁ * sin(α)T₂ᵧ = T₂ * sin(β)W = T₁ * sin(α) + T₂ * sin(β)
También podemos decir que para que el sistema esté en equilibrio, el objeto no debe moverse horizontalmente o a lo largo del eje x. Por lo tanto, las componentes horizontales de T₁ y T₂ deben entonces ser iguales a cero. Además, con la ayuda de la trigonometría, podemos expresar T₁ₓ y T₂ₓ en términos de T₁ y T₂, respectivamente:
T₁ₓ = T₂ₓT₁ * cos(α) = T₂ * cos(β)
Si dividimos ambos lados por cos(α), obtenemos una ecuación en la que T₁ se expresa en términos de T₂ y de los ángulos:
T₁ = T₂ * cos(β) / cos(α)
Entonces podemos utilizar esta ecuación para resolver el T₂ sustituyendo T₂ * cos(β) / cos(α) como el T₁ en nuestra ecuación de suma de fuerzas, como se muestra a continuación:
W = T₁ * sin(α) + T₂ * sin(β)W = T₂ * * sin(α) + T₂ * sin(β)W = T₂ * T₂ = W /
Por último, si multiplicamos toda esta ecuación por cos(β) / cos(α) como derivamos en el valor de T₁ en términos de T₂, y luego simplificamos todo, obtenemos esta ecuación:
T₁ = W / * T₁ = W / * T₁ = W /
Ahora todo lo que necesitas saber son los ángulos de las cuerdas de tensión con respecto a la horizontal. Si se da un ángulo con respecto a la vertical, basta con restar este ángulo a 90°. Así obtendrás el ángulo con respecto a la horizontal. Sin embargo, si te dan otros valores de ángulos que pueden ser mayores de 90° o incluso de 180°, puedes consultar nuestra calculadora de ángulos de referencia para ayudarte a determinar el ángulo que necesitas. Después de determinar los valores de las variables en nuestras fórmulas de fuerza de tensión, ahora podemos resolver las fuerzas de tensión.