Variansen är ett tal som anger hur långt en uppsättning siffror ligger ifrån varandra.Variansen är identisk med den kvadrerade standardavvikelsen och uttrycker därför ”samma sak” (men starkare).
Varians – exempel
En studie låter 100 personer utföra en enkel hastighetsuppgift under 80 försök. För varje deltagare registreras således 80 reaktionstider (i sekunder). En del av dessa data visas nedan.

I studier som dessa ser vi vanligtvis att människor blir snabbare när de utför hastighetsuppgiften oftare. Det vill säga, den genomsnittliga reaktionstiden tenderar att minska över försök.
Också, reaktionstiderna kommer typiskt sett att variera mindre mellan olika personer i den mån de utför uppgiften oftare. Tekniskt sett säger vi att variansen minskar över försök. Tabellen nedan illustrerar detta för försök 1,4,7 och 10.
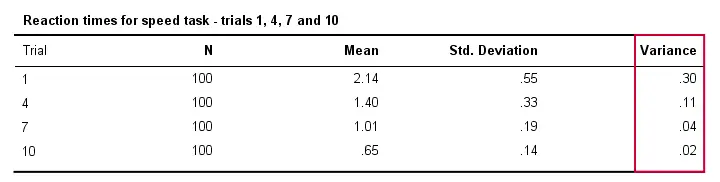
Varians och histogram
Ett bra sätt att visualisera data från vår tidigare tabell är ett histogram för varje försök. På så sätt illustrerar figuren nedan att deltagarna blev snabbare över försök; från försök 1 till försök 10 rör sig histogrambalkarna åt vänster, mot 0 sekunder.
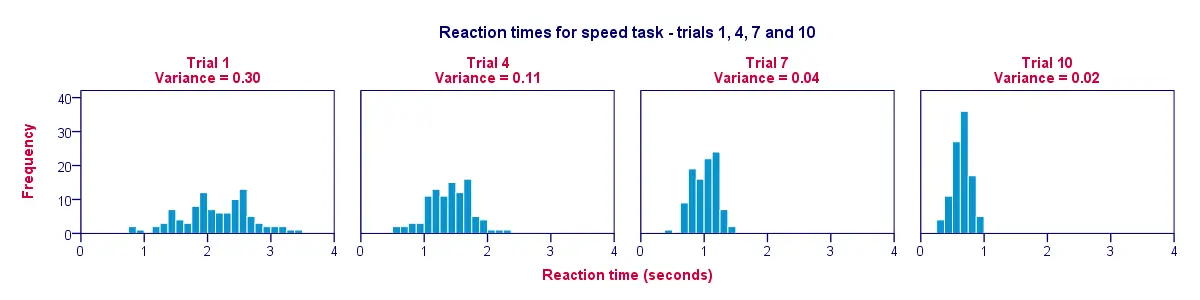
En annan upptäckt är att histogrammen blir smalare (och därmed högre) när vi rör oss från försök 1 till försök 10. Detta illustrerar att reaktionstiderna varierar mindre och mindre mellan våra deltagare allteftersom experimentet fortskrider. Variansen minskar över försök.
Varians – populationsformel
En grundläggande formel för att beräkna variansen är
$$$S^2 = \frac{\sum(X – \overline{X})^2}{n}$$$
Vi rekommenderar att du försöker förstå vad den här formeln gör, eftersom det hjälper en hel del till när du ska förstå ANOVA (= analys av varians). Vi kommer därför att demonstrera den på en handfull data.
Varians – GoogleSheets
För enkelhetens skull skär vi ner våra data till det första försöket för de fem första deltagarna. Dessa 5 reaktionstider – och en manuell beräkning av deras varians – finns i detta GoogleSheet.
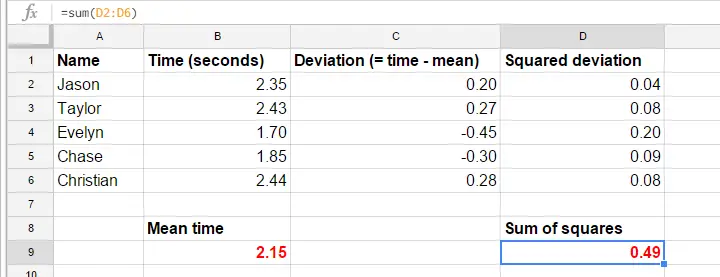
Varians – Beräkningssteg
Formlerna i GoogleSheet visar exakt hur man beräknar en varians. De grundläggande stegen är
- beräkna den genomsnittliga reaktionstiden (2,15);
- beräkna avvikelsepoäng (reaktionstid minus genomsnittlig reaktionstid);
- beräkna kvadrerade avvikelsepoäng;
- addera kvadrerade avvikelsepoäng. Resultatet (0,49) är en kvadratsumma, den viktigaste byggstenen i ANOVA;
- dividera kvadratsumman med antalet observationer (5 reaktionstider).
Alternativt kan du beräkna en varians genom att skriva =VARP(B2:B6) i någon cell (B2:B6 är cellerna som innehåller våra 5 reaktionstider). VARP är en förkortning för ”varianspopulation”. OpenOffice och MS Excel innehåller liknande formler.
Varians – Provformel
Som standardavvikelsen, om våra data är ett enkelt slumpmässigt urval från en mycket större population, kommer den tidigare nämnda formeln systematiskt att underskatta populationsvariansen. I detta fall använder vi en något annorlunda formel:
$$$$S^2 = \frac{\sum(X_i – \overline{X})^2}{n – 1}$$$
Vilken formel vi ska använda beror alltså på våra data: innehåller de hela populationen som vi vill undersöka eller är de bara ett stickprov från denna population?
Då våra 100 deltagare helt klart är ett stickprov, använder vi stickprovsformeln. I GoogleSheets kan man skriva =VAR(B2:B6) i en cell för att få fram stickprovsvariansen.
Varians i SPSS
Såvitt vi vet saknas formeln för populationsvariansen helt i SPSS och vi anser att detta är en allvarlig brist. Istället använder SPSS alltid stickprovsformeln. detta gäller både för variansen mellan försökspersoner (som diskuteras i denna handledning) och variansen inom försökspersoner. Relevant utdata visas nedan.

När det gäller den här utdatatabellen kan man också notera att variansen faktiskt är den kvadrerade standardavvikelsen (bortsett från avrundning).
När det gäller variansen, så är det ungefär så. Vi hoppas att den här handledningen hjälpte dig att förstå vad en varians är.