Oönskad konvolution är ett inneboende problem vid överföring av analog information. Exempelvis kan allt följande modelleras som en konvolution: bildförvrängning i en skakig kamera, ekon i långdistanssamtal, den obegränsade bandbredden hos analoga sensorer och analog elektronik osv. Dekonvolution är processen att filtrera en signal för att kompensera för en oönskad konvolution. Målet med dekonvolutionen är att återskapa signalen så som den var innan konvolutionen ägde rum. Detta kräver vanligen att man känner till egenskaperna för konvolutionen (dvs. impulssvaret eller frekvenssvaret). Detta kan särskiljas från blind dekonvolution, där egenskaperna hos den parasitära konvolutionen inte är kända. Blind dekonvolution är ett mycket svårare problem som inte har någon allmän lösning, och tillvägagångssättet måste anpassas till den särskilda tillämpningen.
Dekonvolution är nästan omöjlig att förstå i tidsdomänen, men ganska enkel i frekvensdomänen. Varje sinusoid som utgör den ursprungliga signalen kan ändras i amplitud och/eller fas när den passerar genom den oönskade konvolutionen. För att få fram den ursprungliga signalen måste dekonvolutioneringsfiltret upphäva dessa amplitud- och fasförändringar. Om konvolutionen t.ex. ändrar en sinusoidens amplitud med 0,5 med en fasförskjutning på 30 grader, måste dekonvolutioneringsfiltret förstärka sinusoiden med 2,0 med en fasförskjutning på -30 grader.
Det exempel som vi kommer att använda för att illustrera dekonvolutionen är en gammastrålningsdetektor. Som illustreras i figur 17-3 består denna anordning av två delar, en scintillatoroch en ljusdetektor. En scintillator är en speciell typ av genomskinligt material, t.ex. natriumjodid eller bismutgermanat. Dessa föreningar omvandlar energin i varje gammastråle till en kort stöt av synligt ljus. Detta ljus
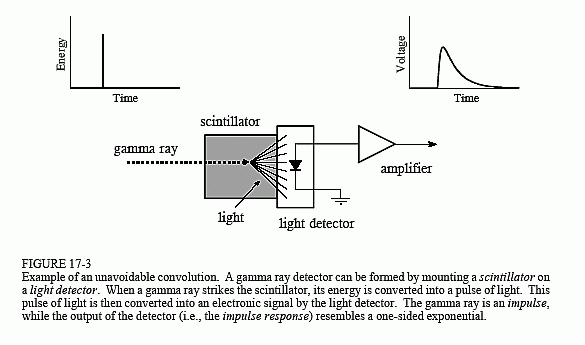
omvandlas sedan till en elektronisk signal av en ljusdetektor, till exempel en fotodiod eller ett fotomultiplikatorrör. Varje puls som produceras av detektorn liknar en ensidig exponential, med en viss avrundning av hörnen. Denna form bestäms av egenskaperna hos den använda scintillatorn. När en gammastråle avger sin energi i scintillatorn exciteras närliggande atomer till en högre energinivå. Dessa atomer avexciteras slumpmässigt, var och en av dem producerar en enda foton synligt ljus. Nettoresultatet är en ljuspuls vars amplitud avtar under några hundra nanosekunder (för natriumjodid). Eftersom ankomsten av varje gammastråle är en impuls är utgångspulsen från detektorn (dvs. den ensidiga exponentialen) systemets impulssvar.
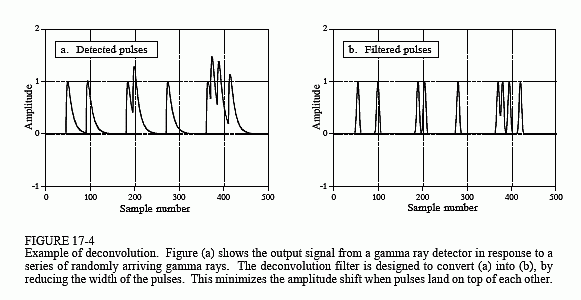
Figur 17-4a visar impulser som genereras av detektorn som svar på slumpmässigt ankommande gammastrålar. Den information som vi vill utvinna ur denna utsignal är amplituden för varje puls, som är proportionell mot energin hos den gammastråle som genererade den. Detta är användbar information eftersom energin kan berätta intressanta saker om var gammastrålen har varit. Den kan t.ex. ge medicinsk information om en patient, ange åldern på en avlägsen galax, upptäcka en bomb i ett flygplansbagage osv.
Allt skulle vara bra om bara enstaka gammastrålar upptäcktes, men så är oftast inte fallet. Som visas i (a) kan två eller flera pulser överlappa varandra och förskjuta den uppmätta amplituden. Ett svar på detta problem är att avveckla detektorns utsignal och göra pulserna smalare så att det inte uppstår så mycket överlappning. Helst skulle vi vilja att varje puls liknar den ursprungliga impulsen. Som du kanske anar är detta inte möjligt och vi måste nöja oss med en puls som är ändligt lång, men betydligt kortare än den detekterade pulsen. Detta mål illustreras i figur 17-4b.
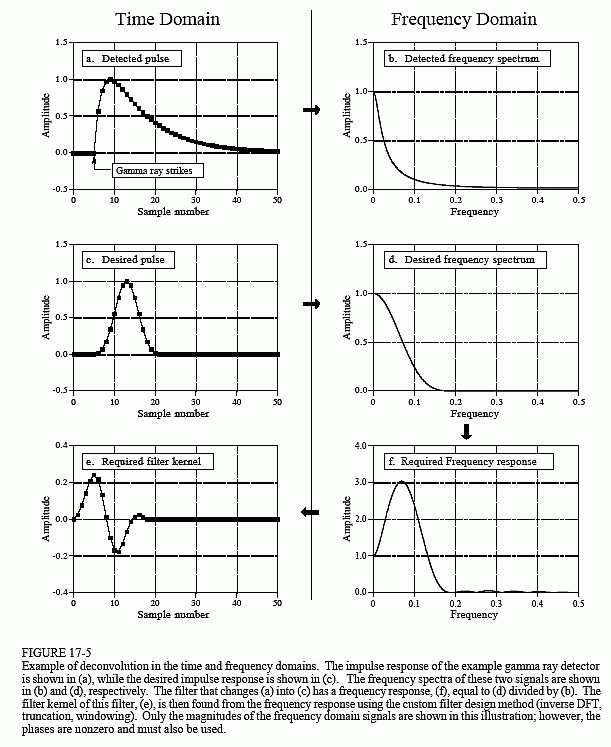
Även om detektorsignalen har sin information kodad i tidsdomänen måste en stor del av vår analys göras i frekvensdomänen, där problemet är lättare att förstå. Figur 17-5a är signalen som produceras av detektorn(något vi känner till). Figur (c) är den signal som vi vill ha (också något vi vet). Denna önskade puls valdes godtyckligt till att ha samma form som ett Blackmanfönster, med en längd på ungefär en tredjedel av den ursprungliga pulsen. Vårt mål är att hitta en filterkärna, (e), som när den konvolveras med signalen i (a) ger signalen i (c). I ekvationsform: om a * e = c, och givet a och c, hitta.
Om dessa signaler kombinerades genom addition eller multiplikation i stället för konvolution skulle lösningen vara enkel: subtraktion används för att ”av-addera” och division används för att ”av-multiplicera”. Konvolution är annorlunda; det finns ingen enkel omvänd operation som kan kallas ”dekonvolution”. Konvolution är för rörig för att kunna upphävas genom att direkt manipulera signalerna i tidsdomänen.
Turligtvis är detta problem enklare i frekvensdomänen. Kom ihåg att konvolution i en domän motsvarar multiplikation i den andra domänen. Återigen med hänvisning till signalerna i figur 17-5: Om b × f = d, och givet b och d, hitta f. Detta är ett enkelt problem att lösa: Filtrets frekvensrespons, (f), är frekvensspektrumet för den önskade pulsen, (d), dividerat med frekvensspektrumet för den upptäckta pulsen, (b). Eftersom den upptäckta pulsen är asymmetrisk kommer den att ha en fas som inte är noll. Detta innebär att en komplex division måste användas (dvs. en fas av magnitud & dividerad med en annan fas av magnitud &). Om du skulle ha glömt det, så definieras i kapitel 9 hur man utför en komplex division av ett spektrum med ett annat. Den erforderliga filterkärnan, (e), hittas sedan från frekvensresponsen genom den anpassade filtermetoden (IDFT, shift, truncate, &multiplicera med ett fönster).
Det finns gränser för den förbättring som dekonvolutionen kan ge. Med andra ord, om du blir girig kommer saker och ting att falla sönder. Att bli girig i det här exemplet innebär att försöka göra den önskade pulsen överdrivet smal. Låt oss titta på vad som händer. Om den önskade pulsen görs smalare måste dess frekvensspektrum innehålla fler högfrekventa komponenter. Eftersom dessa högfrekvenskomponenter har en mycket låg amplitud i den upptäckta pulsen måste filtret ha en mycket hög förstärkning vid dessa frekvenser. Exempelvis visar (f) att vissa frekvenser måste multipliceras med en faktor tre för att uppnå den önskade pulsen (c). Om den önskade pulsen görs smalare blir förstärkningen av dekonvolutionsfiltret ännu större vid höga frekvenser.
Problemet är att små fel är mycket oförlåtande i denna situation. Om t.ex. en viss frekvens förstärks med 30, när endast 28 behövs, kommer den dekonvolverade signalen förmodligen att bli en enda röra. När dekonvolutionen drivs till högre prestandanivåer måste egenskaperna hos den oönskade konvolutionen förstås med större noggrannhet och precision. Det finns alltid okända faktorer i verkliga tillämpningar som orsakas av sådana skurkar som elektroniskt brus, temperaturavdrift, variation mellan olika apparater osv. Dessa okända faktorer sätter en gräns för hur väl dekonvolutionen kommer att fungera.
Även om den oönskade konvolutionen är perfekt förstådd finns det fortfarande ett faktum som begränsar dekonvolutionens prestanda: brus. De flesta oönskade konvolutioner har till exempel formen av ett lågpassfilter som minskar amplituden av signalens högfrekvenskomponenter. Dekonvolutionen korrigerar detta genom att förstärka dessa frekvenser. Om amplituden för dessa komponenter faller under systemets inneboende brus går dock den information som finns i dessa frekvenser förlorad. Ingen signalbehandling kan återskapa den. Den är borta för alltid. Adios! Adjö! Sayonara! Att försöka återvinna dessa data kommer bara att förstärka bruset. I extremfallet kan amplituden för vissa frekvenser helt reduceras till noll. Detta utplånar inte bara informationen, utan kommer också att försöka få avvecklingsfiltret att få oändlig förstärkning vid dessa frekvenser. Lösningen: konstruera ett mindre aggressivt avvecklingsfilter och/eller sätta gränser för hur mycket förstärkning som tillåts vid någon av frekvenserna.
Hur långt kan man gå? Hur girig är för girig? Detta beror helt och hållet på det problem som du angriper. Om signalen har ett bra beteende och lågt brus kan man förmodligen göra en betydande förbättring (tänk en faktor 5-10). Om signalen förändras med tiden, inte är särskilt välkänd eller bullrig kommer du inte att göra lika bra ifrån dig (tänk en faktor 1-2). För att lyckas med avvecklingen krävs en hel del tester. Om det fungerar på en viss nivå, försök att gå längre; du kommer att veta när det inte fungerar. Inget teoretiskt arbete kommer att göra det möjligt för dig att kringgå denna litterära process.
Dekonvolution kan också tillämpas på frekvensdomän-kodade signaler. Ett klassiskt exempel är restaureringen av gamla inspelningar av den berömda operasångaren Enrico Caruso (1873-1921). Dessa inspelningar gjordes med mycket primitiv utrustning enligt modern standard. Det mest betydande problemet är terresonanserna i det långa rörformade inspelningshornet som användes för att samla in ljudet. När sångaren råkar träffa en av dessa resonansfrekvenser ökar ljudstyrkan i inspelningen plötsligt. Digital dekonvolution har förbättrat den subjektiva kvaliteten på dessa inspelningar genom att
minska de högljudda fläckarna i musiken. Vi kommer endast att beskriva den allmänna metoden; för en detaljerad beskrivning hänvisas till den ursprungliga artikeln: T. Stockham, T. Cannon ochR. Ingebretsen, ”Blind Deconvolution Through Digital Signal Processing”,Proc. IEEE, vol. 63, Apr. 1975, pp. 678-692.
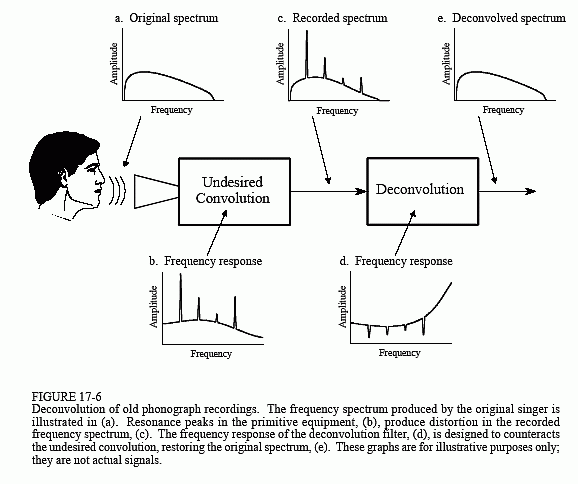
Figur 17-6 visar den allmänna metoden. Frekvensspektrumet för den ursprungliga ljudsignalen illustreras i (a). Figur (b) visar inspelningsutrustningens frekvensrespons, en relativt jämn kurva med undantag för flera skarpa resonanstoppar. Den inspelade signalens spektrum, som visas i (c), är lika med det sanna spektrumet, (a), multiplicerat med den ojämna frekvensresponsen, (b). Målet med avvecklingen är att motverka den oönskade avvecklingen. Med andra ord måste frekvensresponsen för dekonvolutionsfiltret,(d), vara den omvända delen av (b). Det vill säga, varje topp i (b) upphävs av en motsvarande sänkning i (d). Om detta filter var perfekt utformat skulle den resulterande signalen ha ett spektrum, (e), som är identiskt med originalets.
Här är haken: den ursprungliga inspelningsutrustningen har sedan länge kasserats, och dess frekvensrespons, (b), är ett mysterium. Med andra ord är detta ett problem med blinddekonvolution; om vi bara har (c), hur kan vi då bestämma (d)?
Blinda dekonvolutionsproblem angrips vanligtvis genom att göra en uppskattning eller ett antagande om de okända parametrarna. För att hantera detta exempel antas att den ursprungliga musikens genomsnittliga spektrum motsvarar det genomsnittliga spektrumet för samma musik som framförs av en sångare i dag med modern utrustning. Det genomsnittliga spektrumet hittas med hjälp av tekniken i kapitel 9: dela upp signalen i ett stort antal segment, ta DFT för varje segment, konvertera till polarform och sedan göra ett genomsnitt av storheterna tillsammans. I det enklaste fallet tas det okända frekvensomfånget som det genomsnittliga spektrumet för den gamla inspelningen, dividerat med det genomsnittliga spektrumet för den moderna inspelningen. (Den metod som används av Stockham et al. bygger på en mer sofistikerad teknik som kallas homomorf bearbetning och som ger en bättre uppskattning av inspelningssystemets egenskaper).