Hur man beräknar spänningen i linor som hänger upp ett föremål
Vi kan se i illustrationen nedan att kraften, F, som behövs för att lyfta föremålet är lika med föremålets vikt, W. Denna idé är det grundläggande koncept som ligger till grund för vår formel för spänningskraft. Nedan visas också föremålets frikroppsdiagram som visar de spänningskrafter, T, som verkar i snöret. Som du kan se kommer spänningskrafterna i par och i motsatt riktning:
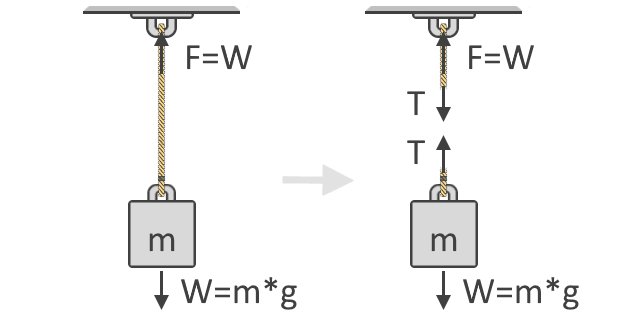
Följande Newtons andra rörelselag kan vi sedan uttrycka summan av krafterna med hjälp av föremålets frikroppsdiagram, vilket visas på högra sidan i illustrationen ovan. Vi använder frikroppsdiagram för att visa de olika riktningarna och storlekarna av de krafter som verkar på en kropp. I jämvikt ska alla dessa krafter vara lika med noll. Om man betraktar alla uppåtriktade krafter som positiva och nedåtriktade som negativa blir vår ekvation:
ΣF = 0 = T + (-W)T = W
där vikten, W, blir negativ eftersom den är riktad nedåt. Genom att överföra W till andra sidan av ekvationen kan vi nu se att spänningskraften i repet är lika med vikten av det föremål som det bär, vilket också visas ovan.
Om vi använder fler rep för att lyfta föremålet blir den totala spänningskraften uppdelad på repen. Spänningskraften i varje rep beror på deras vinklar i förhållande till riktningen av den kraft som det motsätter sig. För att ytterligare förstå detta, låt oss betrakta ett annat frikroppsdiagram av ett föremål som hängs upp av två rep, som visas nedan:
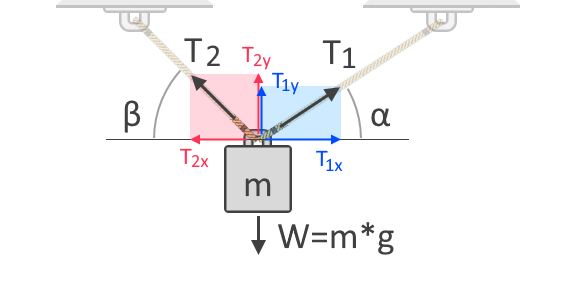
I frikroppsdiagrammet som visas ovan kan vi se spänningskrafternas horisontella och vertikala komponenter, T₁, och T₂. Krafter är vektorer, vilket innebär att de alltid har både storlek och riktning. Liksom alla vektorer kan krafter uttryckas i dessa komponenter vilket ger kraftens påverkan längs den horisontella och vertikala axeln. T₁ₓ och T₂ₓ är de vertikala komponenterna av T₁ respektive T₂. Å andra sidan är T₁ᵧ och T₂ᵧ de vertikala komponenterna av samma krafter. Eftersom gravitationen verkar på föremålet i den vertikala axeln måste vi ta hänsyn till spänningskrafternas vertikala komponenter för vår summering av krafter enligt följande:
ΣF = 0 = T₁ᵧ + T₂ᵧ + (-W)W = T₁ᵧ + T₂ᵧ
Då vi också känner till spänningskrafternas vinklar kan vi uttrycka T₁ᵧ och T₂ᵧ i termer av T₁ respektive T₂ med hjälp av trigonometriska funktioner:
T₁ᵧ = T₁ * sin(α)T₂ᵧ = T₂ * sin(β)W = T₁ * sin(α) + T₂ * sin(β)
Vi kan också säga att för att systemet ska vara i jämvikt får föremålet inte röra sig horisontellt eller längs x-axeln. Därför måste de horisontella komponenterna av T₁ och T₂ då vara lika med noll. Med hjälp av trigonometri kan vi också uttrycka T₁ₓ och T₂ₓ i termer av T₁ respektive T₂:
T₁ₓ = T₂ₓT₁ * cos(α) = T₂ * cos(β)
Om vi delar båda sidorna med cos(α) får vi en ekvation där T₁ uttrycks i termer av T₂ och vinklarna:
T₁ = T₂ * cos(β) / cos(α)
Vi kan sedan använda denna ekvation för att lösa T₂ genom att ersätta T₂ * cos(β) / cos(α) som T₁ i vår ekvation för summering av krafter, enligt nedan:
W = T₁ * sin(α) + T₂ * sin(β)W = T₂ * * sin(α) + T₂ * sin(β)W = T₂ * T₂ = W /
Till sist, om vi multiplicerar hela denna ekvation med cos(β) / cos(α) som vi härledde i värdet av T₁ i termer av T₂, och sedan förenklar allt, får vi denna ekvation:
T₁ = W / * T₁ = W / * T₁ = W /
Nu behöver man bara känna till spänningslinornas vinklar i förhållande till horisontalen. Om en vinkel från vertikalen anges är det bara att subtrahera denna vinkel från 90°. På så sätt får du fram vinkeln från horisontalplanet. Men om du får andra värden på vinklar som kan vara större än 90° eller till och med 180°, kanske du vill kolla in vår referensvinkelkalkylator för att hjälpa dig att bestämma den vinkel du behöver. Efter att ha bestämt värdena för variablerna i våra spänningskraftformler kan vi nu lösa spänningskrafterna.