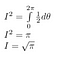Lord Kelvin skrev om detta integral: ”En matematiker är en person för vilken detta är lika självklart som att två gånger två blir fyra för dig.”
Njut 😉
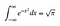
Okej, jag utgår från att du har grundläggande kunskaper om integration och differentiering. Följande kommer att ge lite intuition till smarta knep som kommer senare. Oroa dig inte om en del av det är lite förbryllande, försök bara att få en känsla för vad som händer.
Strategin här kommer att vara att göra en smart substitution. Men vi kommer att göra en substitution i två variabler. Du kan visualisera det aktuella problemet som att beräkna arean under en kurva
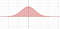
Men vi kommer att visa att problemet kan vändas till att beräkna en volym.
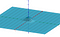
För att beräkna volymen använder vi en något annorlunda formel för byte av variabel än den du använder i vanliga integraler. Vi kommer att använda polära koordinater. Detta uttrycker x- och y-koordinaterna i termer av deras radie och deras vinkel. Geogebra har ett trevligt interaktivt sätt att se det här

Därefter kommer vi att använda den magiska formeln för byte av bas för polarkoordinater.
När vi beräknade arean under kurvan hade vi elementet ”dx” som representerar ett litet avstånd längs x-axeln. När vi beräknar en volym har vi dx dy, vilket är som en liten rektangel med sidlängderna dx och dy. Vi använder sedan dessa baser för att skapa en serie rutor som uppskattar volymen. Detta är lättast att se med visualiseringen nedan. Integralen är gränsen för dessa approximationer.
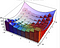
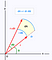
När vi i stället använder polarkoordinatsystemet får vi ett något annorlunda areaelement underifrån. Nedan är dA areaelementet. Med små förändringar i vinkeln och radien kan detta areaelement approximeras allt bättre av en rektangel med sidlängderna dr respektive r*dtheta. Om du är bekväm med lite geometri, för små theta approximeras sin(theta) mycket väl av theta och du kan då bevisa resultatet nedan.
Lösning av integralen
Först ger vi vårt integral ett namn. Vi kallar den I.
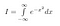
Bemärk att x bara är en ”dummyvariabel”. Området existerar oavsett vilket variabelnamn vi använder. Så vi kan också skriva följande två ekvationer
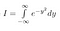
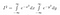
Nu är I bara en konstant, även om det är en som vi inte känner till värdet av ännu, kan vi använda våra normala regler för att föra in en konstant i ett integral
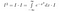
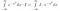
Så långt har vi inte gjort så mycket väsentligt. Nu funderar vi noga på vad integralen betyder. Vi tar integraler av funktioner. Om två funktioner tar samma värde överallt är de likadana och har samma area. Med det i åtanke kan vi göra följande manipulationer, om vi ser I*exp(-x²) som en funktion av x, det vill säga något som tar in värden av x som input, och ger ett tal som output.
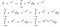
Okej, det var mycket att ta in. I den första raden skrev vi bara om I i dess integralform med ett annat variabelnamn. I den andra raden, där vi behandlade I*exp(-x²) som en funktion, insåg vi att vi kan föra in exp(-x²) innanför dy-integralen, och att detta fortfarande skulle ge samma utgångsvärde för alla ingångsvärden för x. Slutligen använde vi reglerna för exponentiering.
Om vi skriver ut detta i sin helhet har vi nu
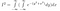
Nästan kommer den mördande insikten. Ovan har vi struntat i variabelnamn och hur man representerar en funktion. Nu byter vi perspektiv: detta uttryck representerar också integralen av exp(-(y²+x²)) över hela 2D-planet, med areaelementet dA = dx dy. Dvs. dx dy är en liten rektangel på ett plan, och exp(-(y²+x²)) är höjden över denna rektangel.
Nästan använder vi polarkoordinaternas insikter från tidigare
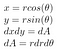
Som sin² + cos² = 1, efter att ha pluggat in allt, får vi
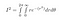
r sträcker sig från 0 till oändlighet och theta sträcker sig från 0 till 2*pi, eftersom detta täcker hela 2D-planet: Varje punkt har en radie som är mindre än oändlig och en vinkel mellan 0 och 2pi radianer.
Vi kan utvärdera det inre integralet med hjälp av kedjeregeln
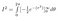
Och, in i det förlovade landet befinner vi oss nu: