När ljuset reflekteras eller transmitteras från en materiell struktur sker en förändring i polarisationen. Ellipsometri mäter denna respons som beror på de optiska egenskaperna och tjockleken hos enskilda material. Ellipsometri används främst för att bestämma optiska konstanter och filmtjocklek, men också för att karakterisera sammansättning, kristallinitet, grovhet, dopingkoncentration och andra materialegenskaper som är förknippade med en förändring av den optiska responsen.

Användningsområden är grundforskning inom fysikaliska vetenskaper, halvledar- och datalagringslösningar, platta bildskärmar, kommunikation, biosensorer och optisk beläggningsindustri. Ellipsometri har också flexibiliteten att mäta de flesta materialtyper: dielektriska material, halvledare, metaller, supraledare, organiska material, biologiska beläggningar och kompositer.

Definition av polariserat ljus

Ljus kan beskrivas som en elektromagnetisk våg som färdas genom rymden. Det sätt på vilket en elektromagnetisk vågs fält beter sig i förhållande till rum och tid kallas för polarisering. Ljus anses vara opolariserat när dess orientering och fas är helt godtyckliga. Ellipsometri mäter dock polariserat ljus – ett elektriskt fält som följer en specifik bana och har en distinkt form i varje given punkt. En elektromagnetisk våg som färdas i z-riktning kan beskrivas med sina x- och y-komponenter, eftersom dess elektriska fält alltid är vinkelrätt mot utbredningsriktningen. När två ortogonala ljusvågor är i fas är det resulterande ljuset linjärt polariserat. Dess orientering bestäms av de relativa amplituderna. Ljuset anses vara cirkulärt polariserat om de ortogonala vågorna är 90° ur fas och har samma amplitud. Den vanligaste polariseringen är elliptisk och kombinerar ortogonala vågor med godtycklig amplitud och fas. Det är här som ellipsometrin har fått sitt namn.

De olika typerna av polarisation:

Linjär

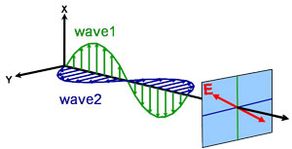
Cirkulär

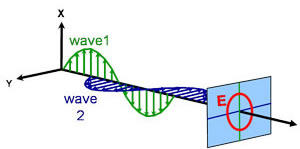
Elliptisk

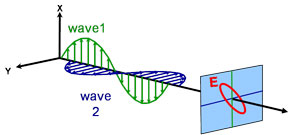
Optiska egenskaper

De optiska egenskaperna, som bestämmer hur ljuset interagerar med ett material, beskrivs av två värden. De representeras i allmänhet som ett komplext tal. Det komplexa brytningsindexet (ñ) består av indexet (n) och en extinktionskoefficient (k):

De optiska egenskaperna kan också avbildas som en komplex dielektrisk funktion:

med följande relation mellan konventionerna:

Indexet beskriver ljusets fashastighet när det färdas i ett material jämfört med ljusets hastighet när det färdas i vakuum, c:

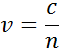
När det går in i ett material med högre index saktar ljuset ner. Eftersom frekvensen hos ljusvågorna inte ändras förkortas våglängden. Förlusten av vågenergi till materialet beskrivs av extinktionskoefficienten som är relaterad till absorptionskoefficienten enligt följande:

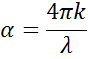
Enligt Beers lag förlorar ljuset intensitet i ett absorberande material. Extinktionskoefficienten visar hur snabbt ljuset försvinner i ett material.

Figur 4 visar en ljusvåg som färdas genom två olika material med varierande egenskaper innan den återvänder till omgivningen.

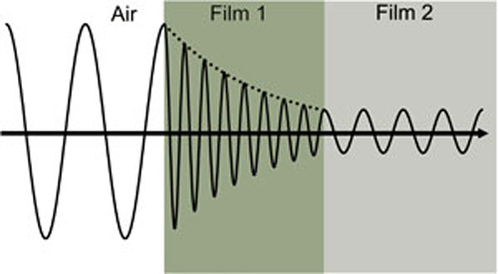
Figur 4: Ljusvågen färdas från luften in i den absorberande filmen 1 och sedan i den transparenta filmen 2. Fashastigheten och våglängden ändras i båda materialen beroende på brytningsindex (Film 1: n=4, Film 2: n=2).

Våglängden bestämmer de optiska konstanterna. Figur 5 visar optiska konstanter för TiO2 från UV till IR. På grund av olika processer som drar energi från ljusvågen sker absorption (k>0) i både UV och IR. IR-absorption orsakas vanligtvis av molekyl- eller fononvibrationer eller fria bärare. UV-absorption sker vanligen på grund av elektroniska övergångar, där ljusenergi exciterar elektroner till förhöjda tillstånd. Figur 5 visar att hypotetiska eller verkliga optiska konstanter inte är oberoende utan matematiskt kopplade genom Kramers-Kronig-relationer.

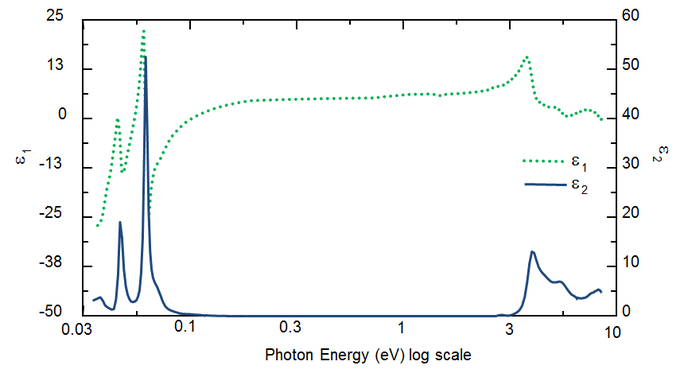
Figur 5: Komplex dielektrisk funktion för TiO2-film med våglängder från IR (små eV) till UV (höga eV).

Ljus- och materialinteraktion

När ljuset interagerar med ett material leder det till gränsförhållanden vid gränssnittet. Under detta måste Maxwells ekvationer alltid förbli uppfyllda. Nedanstående figur visar hur infallande ljus reflekteras och bryts vid gränssnittet. Vinkeln mellan den infallande strålen och provnormalen (θi) blir lika med den reflekterade vinkeln (θr). Ljus som tränger in i ett material bryts i en vinkel θt som ges av:

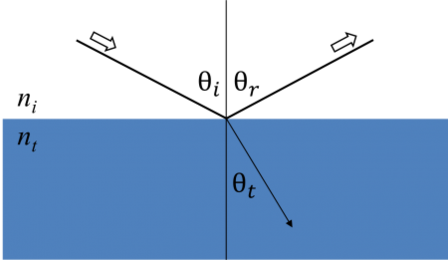
Figur 6: Ljuset reflekteras och bryts enligt Snells lag.

I varje gränssnitt reflekteras en del av ljuset medan resten transmitteras i den brytningsvinkeln. Beroende på randvillkoren gäller olika lösningar för elektriska fält parallellt och vinkelrätt mot provytan. Ljuset kan således delas upp i ortogonala komponenter i förhållande till det infallande planet (p- och s-polariserat). Båda komponenterna kan beräknas separat. Så här beskrev Fresnel mängden ljus som reflekteras och transmitteras vid ett gränssnitt mellan material:

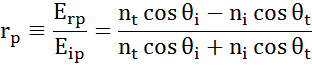
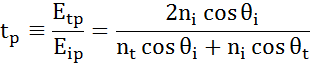
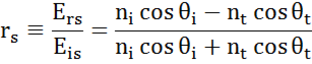
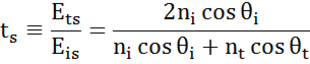
Mångfaldiga gränsytor med korrekta Fresnel-reflektions- och transmissionskoefficienter förekommer med tunna filmer och flerskiktsstrukturer. För att korrekt definiera den reflekterade eller överförda strålen måste den relativa fasen för varje ljuskomponent följas. Filmfasens tjocklek bestäms således på följande sätt:

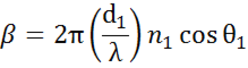
När flera ljusvågor överlagrar varandra uppstår interferens som beror på den relativa fasen hos varje enskild ljusvåg. Nedanstående figur visar kombinationen av ljusvågor i den reflekterade strålen och deras motsvarande Fresnelberäkningar.

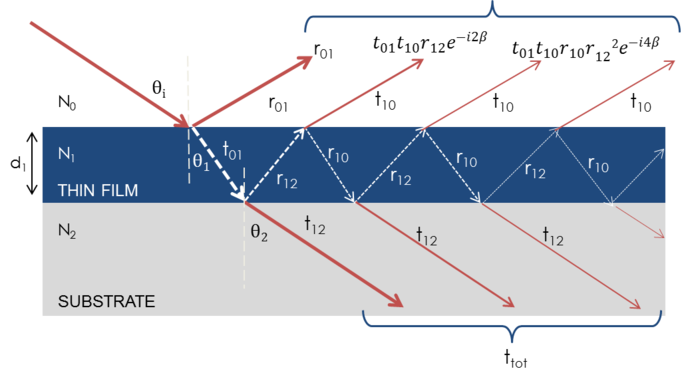
Figur 7: Ljuset reflekteras och bryts vid varje enskilt gränssnitt, vilket leder till flera strålar i en tunn film. Strålinterferens beror på de elektriska fältens relativa fas och amplitud. Strålreaktionen kan beräknas med Fresnelreflektions- och transmissionskoefficienter.

Mätningar

Ellipsometri mäter huvudsakligen hur p- och s-komponenterna reagerar i förhållande till varandra vid reflektion eller transmission. En referensstråle är alltså alltid en del av experimentet. En känd polarisation reflekteras eller transmitteras från provet och utgångspolarisationen mäts. Polarisationsförändringen är ellipsometri-måttet:

Figur 6 visar en typisk ellipsometri-mätning av ett prov. Det linjära infallande ljuset har både p- och s-komponenter. Det reflekterade ljuset visar både amplitud- och fasförändringar för både p- och s- polariserat ljus. Dessa förändringar mäts genom ellipsometri.

För att samla in ellipsometridata behövs följande: ljuskälla, polarisationsgenerator, prov, polarisationsanalysator och detektor. Både polarisationsgeneratorn och analysatorn består av optiska delar som manipulerar polarisationen: kompensatorer, polarisatorer och fasmodulatorer. Typiska ellipsometerkonfigurationer omfattar roterande analysator (RAE), roterande polarisator (RPE), roterande kompensator (RCE) och fasmodulering (PME). Figuren nedan visar en RAE-konfiguration.

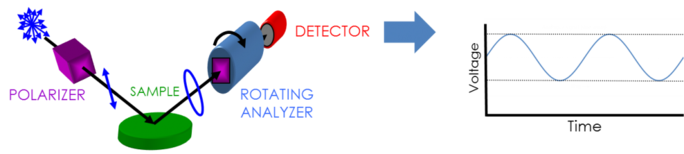
Oppoliserat ljus produceras av en ljuskälla och skickas sedan genom en polarisator. Polarisatorn är inställd så att endast ljus med en viss orientering av det elektriska fältet tillåts passera. Eftersom polarisatorns axel är riktad mellan p- och s-planet når båda provytan. Det nu linjärt polariserade ljuset reflekteras från provytan och blir därmed elliptiskt polariserat och skickas sedan genom en kontinuerligt roterande polarisator (analysatorn). Hur mycket ljus som tillåts passera beror på polarisatorns orientering i förhållande till provets ellips av det elektriska fältet. För att definiera den reflekterade polarisationen omvandlas ljuset till en elektronisk signal i detektorn. Genom att jämföra dessa data med den fastställda ingående polarisationen får man information om den förändring som orsakas av provets reflektion: den ellipsometriska mätningen av Psi och Delta.

Dataanalys

Ellipsometri används för att definiera tjocklek på materialfilmer eller optiska konstanter genom att mäta förändringarna i ljusets polarisering. ”Pseudo”-optiska konstanter från ellipsometri-mätningen kan härledas genom att vända på de data som bestämts för en enda reflektion. Detta är användbart för bulkmaterial.

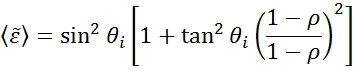
Ovanstående ekvation räknas inte med några ytskikt. Trots detta finns det normalt en ytoxid eller en ojämnhet i bulkmaterial. En direkt inversion kommer att inkludera dessa data som en del av de optiska bulkkonstanterna. Se fig. 10 för en översikt över en typisk dataanalysprocess som används vid ellipsometriska mätningar. Eftersom en exakt ekvation inte kan skrivas är en regressionsanalys nödvändig. Svaret är ofta överbestämt med endast ett fåtal okända och hundratals experimentella datapunkter. En regressionsanalys gör det möjligt att inkludera alla mätdata när lösningen bestäms.

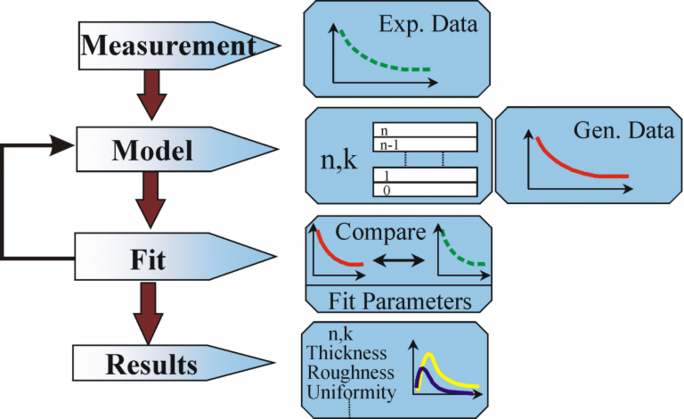
Figur 10: Flödesschema för analys av ellipsometridata.

Följande förfarande används för dataanalys: Provet mäts och en modell görs av provet. Med hjälp av denna modell beräknas de antagna resultaten från Fresnels ekvationer, som beskriver tjocklek och optiska konstanter för varje material. En bedömning av den preliminära beräkningen görs om dessa värden är okända. De beräknade värdena jämförs med experimentella data. För att bättre matcha experimentella data och beräkningsdata kan okända materialdata varieras. De experimentella datapunkterna bör dock alltid vara fler än de okända parametrarna. Exempelvis kan maximalt två materialegenskaper bestämmas med en ellipsometer med en enda våglängd, eftersom den ger exakt två datapunkter: Ψ, Δ (Psi och Delta). Regression används för att hitta den bästa överensstämmelsen mellan modell och experiment. Skillnaden mellan datakurvorna kvantifieras med hjälp av en skattare som medelkvadratfelet (MSE). Okända egenskaper varieras tills det minsta MSE-värdet uppnås. Detta innebär att det lägsta MSE är likvärdigt med det bästa svaret.

Se figuren nedan för MSE-kurvan mot filmtjocklek för en transparent film på kisel. Det lägsta MSE-värdet inträffar vid en tjocklek på 749 nm trots ett antal lokala minima. Den korrekta filmtjockleken är alltså också 749 nm. Regressionsalgoritmen kan anse att ett lokalt minimum är korrekt. För att bestämma det korrekta globala minimumet är det därför klokt att jämföra resultaten med ögat för det lägsta MSE-värdet.

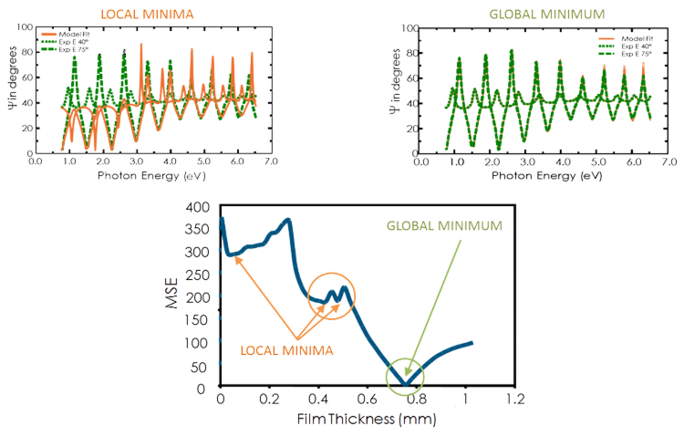
Figur 11, överst till höger: Experimentella data och motsvarande kurvor som genereras för modellen vid det globala minimumet. Figur 11, överst till vänster: En liknande kurva vid det lokala minimumet nära en tjocklek på 0,45 µm kan lätt identifieras som ett felaktigt resultat. Figur 11, nederst: MSE-kurvan mot tjockleken visar det globala minimumet. En regressionsalgoritm kan ge lokala minima, men inte det slutliga resultatet.

Bestämning av filmtjocklek

Filmtjocklek bestäms vanligen av interferensen mellan ljuset som reflekteras från ytan och ljuset som färdas genom filmen. Huruvida denna interferens betraktas som konstruktiv eller destruktiv beror på den relativa fasen hos det ljus som förenas med ytreflektionen. Interferensen innehåller både amplitud- och fasinformation. Fasinformationen från Δ är mycket känslig för filmer ner till submonolagertjocklek. Se figuren nedan för en jämförelse av reflekterad intensitet och ellipsometri för samma serie av tunna SiO2-skikt på Si. Reflektansen för varje film är nästan densamma medan det finns stora variationer i Δ.

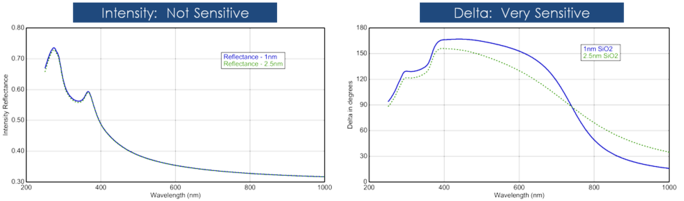
Figur 12, vänster: Reflekterad intensitet och ellipsometriskt delta (höger) för två tunna oxider på kisel. Intensitetsmätningen visar inte att Delta är mycket känsligt för filmer av nanometerstorlek.

Ellipsometri används vanligen för filmer från subnanometer till några mikrometer i tjocklek. Med filmer som är tjockare än flera tiotals mikrometer kan interferensoscillationer endast lösas upp med ökande svårighet, utom när längre infraröda våglängder används. Därför används för tjockare filmer normalt andra mätmetoder.

För att mäta tjockleken måste en del av ljuset färdas genom hela filmen och sedan återvända till ytan. Med ljusabsorberande material kan optiska tjockleksmätningar endast utföras på tunna och halvt ogenomskinliga skikt, om de inte utförs på spektralområden med mindre absorption. En organisk film som absorberar UV- och IR-ljus kan t.ex. vara genomskinlig i mitten av den synliga våglängden. Metaller absorberar starkt vid alla våglängder, så den maximala skikttjockleken som kan bestämmas ligger runt 100 nm.

Optiska konstanter

Optiska konstanter spelar en viktig roll för tjockleksmätningar. En films tjocklek påverkar ljusets väglängd som färdas genom filmen, indexet bestämmer ljusvågens hastighet och brytningsvinkel. Båda bidrar därför till fördröjningen mellan det ljus som färdas genom filmen och ytreflektionen. Det är nödvändigt att fastställa n och k samt tjockleken för att få korrekta resultat från en optisk mätning.

Då ett materials optiska konstanter varierar för olika våglängder måste alla våglängder som analyseras med ellipsometern bestämmas individuellt. Ett materials respons vid varje våglängd kan förutses med hjälp av en tabell över optiska konstanter. För att undvika den mödosamma justeringen av okända optiska konstanter våglängd för våglängd är det fördelaktigt att använda alla våglängder samtidigt. De justerbara parametrarna i en dispersionsrelation gör det till exempel möjligt att anpassa den övergripande formen för den optiska konstanten till de experimentella resultaten. Jämfört med att justera enskilda n och k-värden för varje våglängd minskas antalet okända fria parametrar avsevärt.

Cauchy- eller Sellmeier-relationer används ofta för att beskriva indexet för genomskinliga material där Cauchy-relationen normalt ges som:

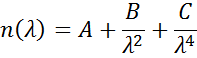
med de tre termerna inpassade för att stämma överens med refraktionsindexet för materialet. Cauchy-sambandet begränsas inte av Kramers-Kronigs (KK) konsistens och kan leda till ofysikalisk spridning. Sellmeierrelationen å andra sidan kräver Kramers-Kronig-konsistens (KK), vilket garanterar att den optiska dispersionen behåller en realistisk form. Sellmeierrelationen skrivs vanligtvis som:

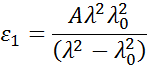
Absorberande material har ofta ett transparent våglängdsområde som kan modelleras med Cauchy- eller Sellmeierrelationen. Medan den absorberande regionen dock måste ta hänsyn till både reella och imaginära optiska konstanter. För att beskriva absorptionen för olika material använder många dispersionsrelationer oscillatorteori, inklusive Lorentz, Harmonic och Gauss, för att beskriva absorptionen för olika material. Alla har liknande egenskaper där absorptionsegenskaperna beskrivs med amplitud, breddning och centrumenergi (relaterat till ljusets frekvens). Formen på den reella komponenten beräknas med hjälp av Kramers-Kronigs konsistens efter att det imaginära beteendet har beskrivits av oscillatorn. För att inkludera eventuell extra absorption utanför det uppmätta spektralområdet läggs en förskjutning till den reella komponenten till. Lorentzoscillatorn kan skrivas som:

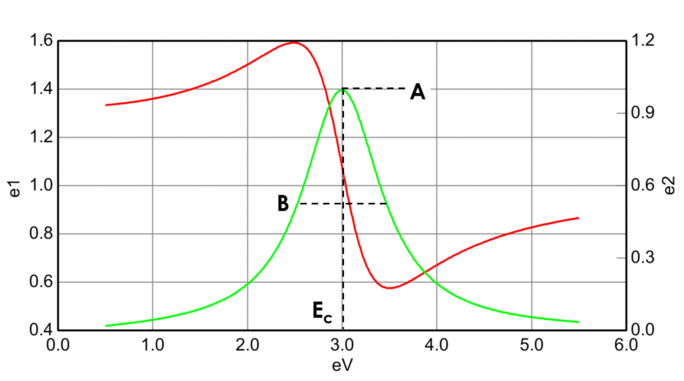
Figur 13 visar också amplitud (A), breddning (B), centrumenergi (Ec) och offset (e1, off set) för en typisk Lorentzoscillator. Energin E är relaterad till en vågs frekvens, n:

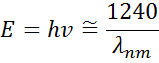
Planckkonstanten h och våglängden λ anges i nanometer. Andra spridningsmodeller, som Tauc-Lorentz och Cody-Lorentz, innehåller termer för att beskriva bandgapsenergin.

Fortsatt läsning

Ellipsometri är en etablerad optisk teknik för mätning av tunna filmer och bulkmaterial. Den använder de polarisationsförändringar som orsakas av reflektion/överföring från en materialstruktur för att bestämma materialets egenskaper som tjocklek och optiska konstanter.

Aspnes D.E. (1985). Exakt bestämning av optiska egenskaper med hjälp av ellipsometri. In: Palik E.D. (red.) Handbook of Optical Constants of Solids, pp. 89-112. Academic Press, Orlando.

Azzam R.M.A. och Bashara N.M. (1987). Ellipsometry and Polarized Light, Elsevier Science B.V., Amsterdam, Nederländerna.

Boccara A.C., Pickering C. och Rivory J. (red.), (1993). Spectroscopic Ellipsometry, Elsevier Publishing, Amsterdam.

Collins R.W., Aspnes D.E. och Irene E.A. (red.), (1998). ”Proceedings from the Second International Conference on Spectroscopic ellipsometry”. In: Thin Solid Films, vols. 313-314.

Fujiwara H., Spectroscopic Ellipsometry, Principles and Applications, John Wiley & Sons, Ltd. 2007

Gottesfeld S., Kim Y.T. och Redondo A. (1995). ”Recent applications of ellipsometry and spectroellipsometry in electrochemical systems”, In: I. Rubinstein (red.), Physical Electrochemistry: Principles, Methods, and Applications, Marcel Dekker, New York.

Herman, I.P. (1996). Optical Diagnostics for Thin Film Processing, s. 425-479. Academic Press, San Diego, Kalifornien.

Johs B. et al (1999). ”Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part II: Advanced Applications”. Optical Metrology, vol. CR72, pp 29-58. SPIE, Bellingham, Washington.

Johs B. et al (2001). ”Recent Developments in Spectroscopic Ellipsometry for in situ Applications”. In: Duparré A, Singh B (red.) Optical Metrology Roadmap for the Semiconductor, Optical, and Data Storage Industries II, vol. 4449, pp 41-57. SPIE, Bellingham, Washington.

Roseler A. (1990). Infrared Spectroscopic Ellipsometry, Akademie-Verlag, Berlin.

Rossow U. och Richter W. (1996). ”Spectroscopic Ellipsometry” i: Bauer G and Richter W (eds.) Optical Characterization of Epitaxial Semiconductor Layers, pp. 68-128, Springer-Verlag, Berlin.

Tompkins H.G. (1993). A User’s Guide to Ellipsometry, Academic Press, San Diego, California.

Tompkins H.G. och McGahan W.A. (1999). Spectroscopic Ellipsometry and Reflectometry, John Wiley & Sons, Inc., USA.

Tompkins, H.G. och Irene E.A. (red.), 2005, Handbook of Ellipsometry, William Andrew Publishing, New York.

Tompkins, H. G. och Hilfiker, J. H., Spectroscopic Ellipsometry, Practical Application to Thin Film Characterization, 2016, Momentum Press Engineering

Woollam J.A. och Snyder P.G. (1992). ”Variable Angle Spectroscopic Ellipsometry” in: Brundle CR, Evans CA och Wilson S (eds) Encyclopedia of Materials Characterization: Surfaces, Interfaces, Thin Films, pp. 401-411, Butterworth-Heinemann, Boston.

Woollam J.A. et al (1999). ”Overview of Variable Angle Spectroscopic Ellipsometry (VASE), Part I: Basic Theory and Typical Applications”. Optical Metrology, vol. CR72, pp 3-28. SPIE, Bellingham, Washington.

Woollam J.A. (2000). ”Ellipsometry, Variable Angle Spectroscopic” i: Webster J.G. (red.) Wiley Encyclopedia of Electrical and Electronics Engineering, pp. 109-116. John Wiley & Sons, New York.