Isingmodellen är ett särskilt exempel på ett termodynamiskt system, och det är ett modellsystem för att förstå fasövergångar. Ni vet hur många biologer ägnar så mycket tid åt miserabla fruktflugor? Tja, fysiker ägnar mycket tid åt Isingmodellen. Som professor Raghu så hjälpsamt berättar för oss är det fasövergångarnas Drosophila.

Personligen är jag inte den största anhängaren av hans analogi eftersom jag tycker att fruktflugor är äckliga. Förhoppningsvis är Isingmodellen inte alltför grov.

Motivation

Varför ska vi ägna så mycket tid åt att prata om Isingmodellen?

• Den är förvånansvärt användbar för att hjälpa oss att tänka på alla sorters beteenden i samband med fasövergångar. Till exempel:

  • Isingmodellen uppvisar symmetribrott i lågtemperaturfasen (vilket vi just talade om)

  • Den har en speciell ”kritisk punkt” vid en väldefinierad temperatur (vilket vi anspelade på i vattens fasdiagram)

  • Andra rika egenskaper.

• Det är en av få exakt lösbara modeller där vi faktiskt kan beräkna termodynamiska kvantiteter och tolka dem.

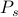  • I allmänhet är det svårt att beräkna termodynamiska kvantiteter eftersom man måste summera många termer. Minns du från vår första termokurs att du kan tänka på ett jämviktssystem som en ensemble av många tillstånd , vart och ett viktat med sin egen sannolikhet . Inom denna ram motsvarar de termodynamiska storheter som du observerar medelvärden över ensemblen. I synnerhet, om du vill hitta ensemblegenomsnittet för någon observerbar 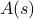, måste du hitta summan 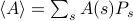, där summan löper över alla möjliga tillstånd. Problemet med detta är, som du minns, att antalet tillstånd i ett termodynamiskt system skalar exponentiellt med antalet partiklar! Även för ett system av måttlig storlek finns det helt enkelt för många tillstånd för att en dator explicit ska kunna beräkna medelvärdet – än mindre ett termodynamiskt system där 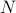är i storleksordningen .

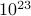  • Så vi måste ”vara smarta” för att beräkna fördelningsfunktionen, och vi borde vara tacksamma för exakt lösbara system!

• Isingmodellen är enkel, men den kan ändå tillämpas på förvånansvärt många olika system.

  • Detta är vårt första smakprov på universalitet – ett kännetecken för kritiska fenomen där samma teori gäller för alla sorters olika fasövergångar, oavsett om det är i vätskor och gaser eller magneter eller supraledare eller vad som helst. Fysiker älskar denna typ av generellt beteende eftersom det tyder på ett slags djupare ordning i vår kaotiska värld.

Definition av Isingmodellen

Isingmodellen är en matematisk modell som inte motsvarar ett verkligt fysiskt system. Det är ett enormt (kvadratiskt) gitter av platser, där varje plats kan befinna sig i ett av två tillstånd. Vi märker varje plats med ett index , och vi kallar de två tillstånden och . För att säga att den :e platsen befinner sig i tillståndet skriver vi .

Nuförtiden är den här definitionen förfärligt abstrakt och ofysikalisk, så för oss fysiker är det oerhört hjälpsamt att ha ett verkligt system i åtanke, så att vi kan hänvisa till något explicit och bygga upp en fysisk intuition. Här är några fysiska system som Ising-modellen kan representera:

• En magnet. Varje plats representerar ett visst ”spinn” i materialet (en oparad elektron??), och det är om spinnet pekar nedåt eller om spinnet pekar uppåt. Var och en av spinnarna fungerar som en minimagnet med ett eget minimagnetmoment; om alla spinnarna är riktade beter sig hela gittret av spinnar som en stor magnet med ett makroskopiskt magnetiskt nettomoment.

• En legering; säg, mässing. Var och en av platserna är en atom i gittret; representerar en kopparatom på den platsen; representerar zink.

• En ”gittergas”. Var och en av platserna är den möjliga platsen för en partikel; betyder att platsen är tom och betyder att platsen är upptagen av en partikel.

• Bakteriella virvelgitter???

För tillfället tänker vi på Isingmodellen som en modell för en magnet. Det är förvisso en grovt förenklad och leksaksmodell av en magnet, men magnetanalogin kan ändå hjälpa oss att vägleda vår omhuldade fysikaliska intuition.

Sätt ihop Hamiltonianen

En naturlig fråga att ställa sig om denna Musse Pigg-modell av en magnet är vilken energi den har. För att vara mer exakt vill vi skriva ner en funktion som representerar energin för varje enskild möjlig konfiguration (även kallad mikrotillstånd) av spinnarna i magneten. Som vi vet kallas denna energifunktion för Hamiltonianen.

I Isingmodellen innehåller Hamiltonianen två typer av interaktioner:

• den externa fälttermen. Som vi minns från kvantmekaniken kan ett externt magnetfält dela upp energierna för spin-down- och spin-up-tillståndet, så att det ena är högre i energi och det andra lägre.

  • Storleken på representerar hur starkt fältet är, så det talar om hur mycket högre energi det ena spinnet är än det andra.

  • Tecknet på talar om om det är spin-up eller spin-down som är att föredra.

  • Då varje enskilt spinn känner av det yttre fältet måste vi summera över alla platser för att hitta det totala bidraget till energin.

• interaktionstermen mellan närliggande spinn – kanske vill de anpassa sig till varandra och peka åt samma håll, kanske vill de antianpassa sig och peka på olika sätt. Fysikaliskt kan vi föreställa oss att denna växelverkan uppstår eftersom varje spinn i magneten är en egen mini-magnetisk dipol som sätter upp sitt eget magnetfält, och dess grannar kan känna det magnetfältet.

  • Storleken på talar om hur starkt grannspins är kopplade till varandra – hur mycket de vill (anti-)alignera. Fysikaliskt sett kan styrkan i spin-spin-kopplingen till exempel bero på avståndet mellan dem i magets gitter.

  • Tecknet på talar om för dig om grannarna föredrar att anpassa sig eller att antianpassa sig. (Den tekniska termen för detta är ferromagnetisk respektive anti-ferromagnetisk). Fysikaliskt sett beror det på de exakta kvantmekaniska detaljerna för hur spinnarna interagerar om ett material är det ena eller det andra (eller ingetdera).

  • Då spinn-spin-interaktionen uppstår mellan två spinn, måste vi summera över par av platser för att hitta dess totala interaktion till energin.

Mer om interaktionstermen

En naturlig fråga om spin-spin-interaktionstermen är vilka spins som är kopplade till vilka spins?

Om vi återgår till den fysiska bilden av magneten, och zoomar in på ett visst spinn, skulle vi förvänta oss att styrkan i spinn-spin-växelverkan är starkare för närliggande spinn och svagare för avlägsna spinn. Det exakta avståndsberoendet för spin-spin-interaktioner är troligen ganska komplicerat för verkliga magneter.

För Isingmodellen gör vi det enklaste möjliga antagandet för arten av denna spin-spin-interaktion:

Några kommentarer:

• I ett kvadratiskt gitter med dimensioner har varje plats 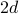närmaste grannar: vänster och höger i en dimension, uppåt och nedåt när man lägger till den andra dimensionen osv…

• Vi utgår från att växelverkan är isotropisk – alla grannar behandlas lika oberoende av riktning.

• Vi talar ofta om närmast-närmaste-granne-interaktioner som energin för en bindning som förenar två gitterplatser.

• När vi summerar över intilliggande par av platser skriver vi symboliskt sett små hakparenteser runt indexen för att representera ”närmaste granne”.

En trevlig konsekvens av närmsta granne-växelverkan är att när vi hittar den totala energin för en viss konfiguration av spinn, i stället för att summera över alla möjliga par av platser, summerar vi bara över par av platser som ligger i anslutning till varandra.

När vi nu har diskuterat alla dessa saker är vi redo att skriva ner det faktiska uttrycket för Hamiltonianen. (Jag ville förklara och tolka fysiken innan jag skrev ner Hamiltonianen så att symbolerna gav någon slags mening.)

Hamiltonianen för Isingmodellen

Hamiltonianen för Isingmodellen kan skrivas som

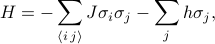
där representerar spinn-spin-växelverkan, representerar det yttre fältet och 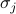är de individuella spinnarna på varje gitterplats. Den första summan är över alla par av angränsande gitterplatser (även kallade bindningar); den representerar växelverkan mellan spinn. Den andra summan är över alla själva gitterplatserna; den representerar det externa fältet som försöker rikta alla spinn i en riktning.

Fortsätt till termodynamiken i Isingmodellen.