av Marco Taboga, PhD
Indikatorfunktionen för en händelse är en slumpmässig variabel som får värdet 1 när händelsen inträffar och värdet 0 när händelsen inte inträffar. Indikatorfunktioner används ofta i sannolikhetsteori för att förenkla notation och för att bevisa satser.

Definition
Följande är en formell definition.
Definition Låt  vara ett samplingsutrymme och
vara ett samplingsutrymme och  vara en händelse. Indikatorfunktionen (eller indikatortillfällighetsvariabeln) för händelsen
vara en händelse. Indikatorfunktionen (eller indikatortillfällighetsvariabeln) för händelsen  , betecknad med
, betecknad med  , är en slumpvariabel som definieras på följande sätt:
, är en slumpvariabel som definieras på följande sätt: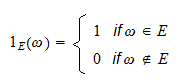
Medan indikatorn för händelsen  vanligtvis betecknas med
vanligtvis betecknas med  , betecknas den ibland också med
, betecknas den ibland också med där
där  är den grekiska bokstaven Chi.
är den grekiska bokstaven Chi.
Exempel Vi kastar en tärning och ett av de sex siffrorna från 1 till 6 kan visas uppåt. Provrummet är Definiera händelsen
Definiera händelsen  som beskrivs av meningen ”Ett jämnt tal visas uppåt”. En slumpvariabel som får värdet 1 när ett jämnt tal visas uppåt och värdet 0 annars är en indikator för händelsen
som beskrivs av meningen ”Ett jämnt tal visas uppåt”. En slumpvariabel som får värdet 1 när ett jämnt tal visas uppåt och värdet 0 annars är en indikator för händelsen  . Den fallvisa definitionen av denna indikator är
. Den fallvisa definitionen av denna indikator är
Från ovanstående definition kan man lätt se att  är en diskret slumpvariabel med stöd
är en diskret slumpvariabel med stöd  och sannolikhetsmassafunktion
och sannolikhetsmassafunktion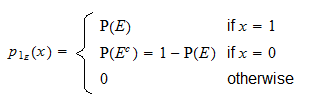
egenskaper
Indikatorfunktioner har följande egenskaper.
Power
Den  -te potensen av
-te potensen av  är lika med
är lika med  :
: om att
om att  kan vara antingen
kan vara antingen  eller
eller  och
och
Förväntat värde
Det förväntade värdet av  är lika med
är lika med  :
: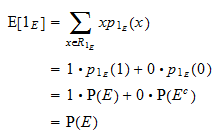
Varians
Variansen för  är lika med
är lika med  . Tack vare den vanliga variansformeln och potensegenskapen ovan får vi
. Tack vare den vanliga variansformeln och potensegenskapen ovan får vi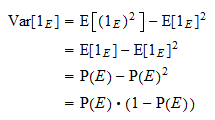
Intersektioner
Om  och
och  är två händelser, så får vi
är två händelser, så får vi på grund av:
på grund av:
-
om
 , då
, då  och
och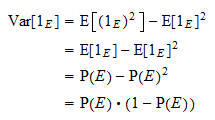
-
om
 , då
, då och
och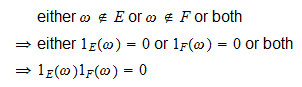
Indikatorer för händelser med noll sannolikhet
Låt  vara en händelse med noll sannolikhet och
vara en händelse med noll sannolikhet och  en integrerbar slumpvariabel. Då,
en integrerbar slumpvariabel. Då, Även om ett rigoröst bevis för detta faktum ligger utanför räckvidden för denna inledande redogörelse, bör denna egenskap vara intuitiv. Den slumpmässiga variabeln
Även om ett rigoröst bevis för detta faktum ligger utanför räckvidden för denna inledande redogörelse, bör denna egenskap vara intuitiv. Den slumpmässiga variabeln  är lika med noll för alla provpunkter
är lika med noll för alla provpunkter  utom möjligen för punkterna
utom möjligen för punkterna  . Det förväntade värdet är ett viktat medelvärde av de värden
. Det förväntade värdet är ett viktat medelvärde av de värden  kan anta, där varje värde viktas med sin respektive sannolikhet. De värden som inte är noll och som
kan anta, där varje värde viktas med sin respektive sannolikhet. De värden som inte är noll och som  kan anta viktas med noll sannolikheter, så
kan anta viktas med noll sannolikheter, så  måste vara noll.
måste vara noll.
Lösta övningar
Nedan hittar du några övningar med förklarade lösningar.
Övningsuppgift 1
Betrakta en slumpvariabel  och en annan slumpvariabel
och en annan slumpvariabel  som är definierad som en funktion av
som är definierad som en funktion av  .
.
Uttryck  med hjälp av indikatorfunktionerna för händelserna
med hjälp av indikatorfunktionerna för händelserna  och
och  .
.
Notera med  indikatorn för händelsen
indikatorn för händelsen  och notera med
och notera med  indikatorn för händelsen
indikatorn för händelsen  . Vi kan skriva
. Vi kan skriva  som
som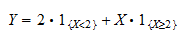
Övningsuppgift 2
Låt  vara en positiv slumpvariabel, det vill säga en slumpvariabel som endast kan anta positiva värden. Låt
vara en positiv slumpvariabel, det vill säga en slumpvariabel som endast kan anta positiva värden. Låt  vara en konstant. Bevisa att
vara en konstant. Bevisa att  där
där  är indikatorn för händelsen
är indikatorn för händelsen  .
.
Bemärk först att summan av indikatorerna  och
och  alltid är lika med
alltid är lika med  :
: Som en följd av detta kan vi skriva
Som en följd av detta kan vi skriva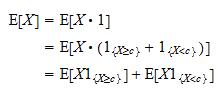 Bemärk nu att
Bemärk nu att  är en positiv slumpvariabel och att det förväntade värdet av en positiv slumpvariabel är positivt:
är en positiv slumpvariabel och att det förväntade värdet av en positiv slumpvariabel är positivt: Det innebär att
Det innebär att 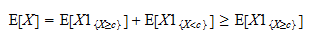
Övningsuppgift 3
Låt  vara en händelse och beteckna dess indikatorfunktion med
vara en händelse och beteckna dess indikatorfunktion med  . Låt
. Låt  vara komplementet till
vara komplementet till  och beteckna dess indikatorfunktion med
och beteckna dess indikatorfunktion med  . Kan du uttrycka
. Kan du uttrycka  som en funktion av
som en funktion av  ?
?
Summan av de två indikatorerna är alltid lika med  :
: Därför,
Därför,
How to cite
Please cite as:
Taboga, Marco (2017). ”Indicator functions”, Lectures on probability theory and mathematical statistics, tredje upplagan. Kindle Direct Publishing. Online appendix. https://www.statlect.com/fundamentals-of-probability/indicator-functions.