Hur gör vi en Guinier-anpassning?¶
Guinier-approximationen gäller endast när exponentialen \(\exp(-q^2 R_g^2 /3)\)är liten. Detta innebär att för att göra en bra Guinieranpassning måsteqRg vara tillräckligt liten. Det qRg-värde vid vilket Guinier-approximationen börjar misslyckas för en given spridningsprofil beror på spridarens övergripande form. Nedan visas en figur som visar Guinier-approximationen (svart) och spridningsintensiteten för en sfär, en tunn stav och en tunn skiva (alla med samma Rg).
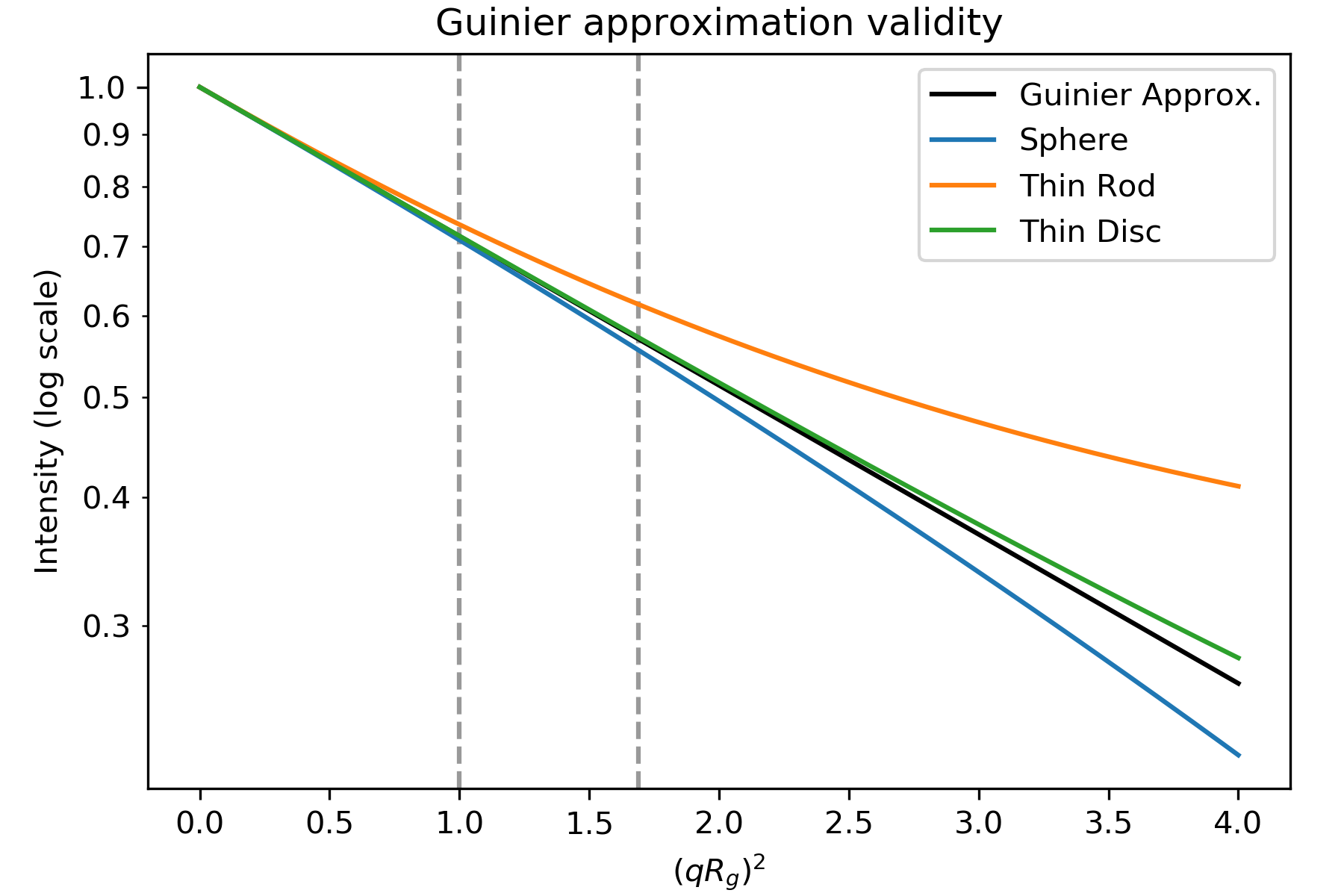
Plott baserad på figur 3.3 i . Intensitet för de geometriska formerna från tabell 3.4 i . Streckade linjer är vid qRg 1,0 och 1,3((qRg) 2 1,0 och 1,69).
Som ni kan se stämmer spridningsintensiteten för staven endast överens med Guinier-approximationen fram till \(qR_g\sim 1,0\), klotet fram till \(qR_g\sim 1,3\) och skivan fram till \(qR_g\sim 1,7\). Beroende på den övergripande partikelformen bör man alltså anpassa olika mängder data med låg q för att få en bra Guinieranpassning. (Observera: Plottets x-axel är (qRg) 2, så \(qR_g\sim 1,3\) visas som den streckade linjen vid 1,69)
I praktiken anpassar vi både klotformiga (sfärliknande och skivliknande) objekt fram till \(qR_g\sim 1,3\), medan vi anpassar starkt utsträckta (stavliknande) objekt fram till \(qR_g\sim 1,0\). Dessa värden valdes för att få <10 % fel som beror på avvikelsen mellan den faktiska formen och Guinier-approximationen.Anledningen till att vi accepterar en så stor avvikelse är att man också får en osäkerhet när man anpassar färre punkter i sina data, så det finns en kompromiss mellan hur väl approximationen fungerar (anpassning till mindre maximalt qRg) och hur väl man kan anpassa sina data (anpassning till större maximalt qRg).
Guinieranpassningens räckvidd är alltså idealt sett från det tidigaste tillgängliga q-värdet till ett maximalt qRg på 1,0 eller 1,3. Med tanke på att Rg härleds från Guinieranpassningen, hur bestämmer man då det korrekta maximala q-värdet för slutet av anpassningen? Svaret är att Guinieranpassningen görs iterativt:
- Bestäm ett maximalt q-värde som startvärde för anpassningen.
- Beräkna Guinieranpassningen och få Rg.
- Om qmaxRg > 1,3 (eller 1,0), minska det maximala q-värdet. OmqmaxRg < 1,3 (eller 1,0), öka det maximala q-värdet.
- Upprepa steg 2 och 3 tills du konvergerar mot ett slutgiltigt maximalt q-värde.
De flesta programvaror nuförtiden gör denna iterativa sökning åt dig, och för data av god kvalitet får du ett rimligt maximalt q-värde som kanske bara behöver förfinas lite manuellt.
Minimalt q-värde för en Guinieranpassning bestäms vanligen av det minsta tillgängligaq-värdet i dina data, som ställs in av instrumentet som du gör mätningen på.Det är dock viktigt att ha ett tillräckligt litet minimalt q-värde för att ha en rimlig räckvidd för Guinieranpassningen. Vanligtvis bör det minsta qRg-värdet vara\(qR_g\leq 0,65\), men för globulära system kan det vara okej att ha\(qR_g\leq 1,0\). Detta innebär att det minsta q-värdet som krävs beror på storleken på det uppmätta systemet. I vissa fall, när det gäller särskilt stora system, kan det hända att man medvetet måste leta efter ett instrument som kan mäta till ett tillräckligt lågt q.
Om dina data har kvalitetsproblem vid lågt q, vilket kan orsakas av de problem som anges ovan, kan det hända att du upptäcker att om du utesluter dessa data från anpassningen så kan du förbättra kvaliteten på anpassningen. Även om detta kan vara acceptabelt bör du vara försiktig när du gör det och alltid visa hela dataområdet i diagrammen.Det mest acceptabla fallet för detta är när de första punkterna är antingen för höga eller för låga, men resten av området passar perfekt (se nedan för kriterier för en bra anpassning). I det fallet kan de par punkter som ligger närmast strålstoppet ha dålig statistik eller högre instrumentell bakgrundsspridning, och kan vanligtvis ignoreras utan risk.