Somliga händelser som äger rum i ett kontinuerligt provrum kan åberopa geometriska bilder av minst två anledningar: på grund av problemets natur eller på grund av lösningens natur.

Vissa problem, som Buffons nål, Birds On a Wire, Bertrands paradox eller problemet med en pinne som bryts i tre delar, uppstår till sin natur i en geometrisk miljö. Det sistnämnda problemet kan också omformuleras på flera sätt, vilket kräver en jämförelse av areorna av geometriska figurer. I allmänhet kan vi tänka oss geometriska sannolikheter som icke-negativa kvantiteter (som inte överstiger 1) som tilldelas delområden av ett givet område enligt vissa regler. Om funktionen μ är ett uttryck för denna tilldelning definierad på en domän D, kräver vi till exempel

0 ≤ μ(A) ≤ 1, A ⊂ D och
μ(D) = 1

Funktionen μ är vanligen inte definierad för alla A ⊂ D. De delmängder av D för vilka μ är definierad är de slumpmässiga händelser som bildar en viss provyta. Mycket ofta definieras μ med hjälp av förhållandet mellan områden så att om σ(A) definieras som ”området” för mängden A, så kan man sätta μ(A) = σ(A) / σ(D).

Problem 1

Två vänner som tar tunnelbanan till sina arbeten från samma station anländer till stationen enhetligt slumpmässigt mellan klockan 7 och 7:20 på morgonen. De är villiga att vänta på varandra i 5 minuter, varefter de tar ett tåg antingen tillsammans eller ensamma. Vad är sannolikheten för att de möts på stationen?

I ett kartesiskt koordinatsystem (s, t) representerar en kvadrat med sidan 20 (minuter) alla möjligheter att de två vännerna anländer till tunnelbanestationen på morgonen.

Den grå ytan A avgränsas av två räta linjer, t = s + 5 och t = s – 5, så att inom A är |s – t| ≤ 5. Av detta följer att de två vännerna kommer att träffas endast under förutsättning att deras ankomster s och t faller inom område A. Sannolikheten för att detta ska inträffa ges av förhållandet mellan arean av A och arean av kvadraten:

/ 400 = 175/400 = 7/16.

Problem 2

(.)

Tre punkter A, B, C placeras slumpmässigt på en cirkel med radie 1. Vad är sannolikheten för att ΔABC är spetsigt?.

Fixera punkten C. Punkterna A och B:s positioner definieras då av bågar α och β som sträcker sig från C i två riktningar. På förhand vet vi att 0 < α + β < 2π. De för vårt problem gynnsamma värdena för α och β (som subtenderande spetsiga vinklar uppfyller) 0 < α < π och 0 < β < π. Deras summa kan inte vara mindre än π eftersom detta skulle göra vinkeln C trubbig, därför är α + β > π. Situationen presenteras i följande diagram där kvadraten har sidan 2π.

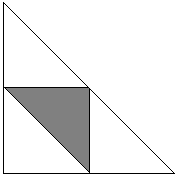
Region D är skärningspunkten mellan tre halvplan: 0 < α, 0 < β och α + β < 2π. Detta är den stora triangeln i diagrammet ovan. De gynnsamma händelserna hör till den skuggade triangeln som är skärningspunkten mellan halvplanen α < π, β < π och α + β > π. Förhållandet mellan areorna av de två är uppenbarligen 1/4.

Observera nu att om inte den slumpmässiga triangeln är spetsig kan den betraktas som trubbig eftersom sannolikheten för att två av de tre punkterna A, B, C bildar en diameter är 0. (För att BC ska vara en diameter bör man ha α + β = π vilket är en rät linje, med noll som enda möjliga tilldelning av area). Vi kan alltså säga att sannolikheten för att ΔABC är trubbig är 3/4. För en trubbig triangel kan cirkeln delas upp i två halvor där triangeln ligger helt och hållet i en av halvorna. Av detta följer att 3/4 är svaret på följande fråga:

Tre punkter A, B, C placeras slumpmässigt på en cirkel med radie 1. Hur stor är sannolikheten att alla tre ligger i en halvcirkel?

1. E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Five Hundred Mathematical Challenges by (MAA, 1995, problem 244.)
2. D. A. Klain, G.-C. Rota Introduction to Geometric Probability , Cambridge University Press, 1997
3. A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions, Dover, 1978
4. A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Geometrisk sannolikhet

• Geometriska sannolikheter
• Är de flesta trianglar trubbiga?
  • Åtta val i sex sektorer
  • Tre slumpmässiga punkter på en cirkel
• Geometrisk sannolikhet
  • Pinne som är uppdelad i tre delar (trilinjära koordinater)
  • Pinne som är uppdelad i tre delar. Lösning i kartesiska koordinater
• Bertrands paradox
• Fåglar på en tråd (problem och interaktiv simulering)
  • Fåglar på en tråd: Lösning av Nathan Bowler
  • Birds on a Wire. Lösning av Mark Huber
  • Birds on a Wire: en probabilistisk simulering. Lösning av Moshe Eliner
  • Birds on a Wire. Lösning av Stuart Anderson
  • Birds on a Wire. Lösning av Bogdan Lataianu
• Buffon’s Noodle Simulation
• Averaging Raindrops – an exercise in geometric probability
  • Averaging Raindrops, Part 2
• Rectangle on a Chessboard: En introduktion
• Markera och bryta pinnar
• Frivilliga punkter på ett segment
• Täckning av en halvcirkel
• Täckning av en halvkula
• Överlappande slumpmässiga intervaller
• Slumpmässiga intervall
• Slumpmässiga intervaller med en dominerande
• Punkter på ett kvadratiskt rutnät
• Flacka sannolikheter på en sfär
• Sannolikhet i en triangel

|Kontakt||Framsidan|Innehåll|Uppåt|

Copyright © 1996-2018 Alexander Bogomolny