Vad är formen för lutning och intercept

Form för lutning och intercept är en av de tre former som vi kan använda för att uttrycka en rät linje. De andra formerna kallas för punkt- och lutningsform och standardform, men vi kommer främst att använda lutning-interceptform i det här avsnittet. Med hjälp av slope intercept form uttrycker vi ekvationen för en linje som:

y=mx+by = mx + by=mx+b

Du kanske vet att xxx och yyy är koordinater för en punkt på en graf, men vad är mmm och bbb?

Vad är b i y=mx+b?

Bokstaven b är en siffra som anger när linjen berör y-axeln. Vi hänvisar också till detta som ”y-interceptet”. Låt oss till exempel rita en rät linje på koordinatplanet.

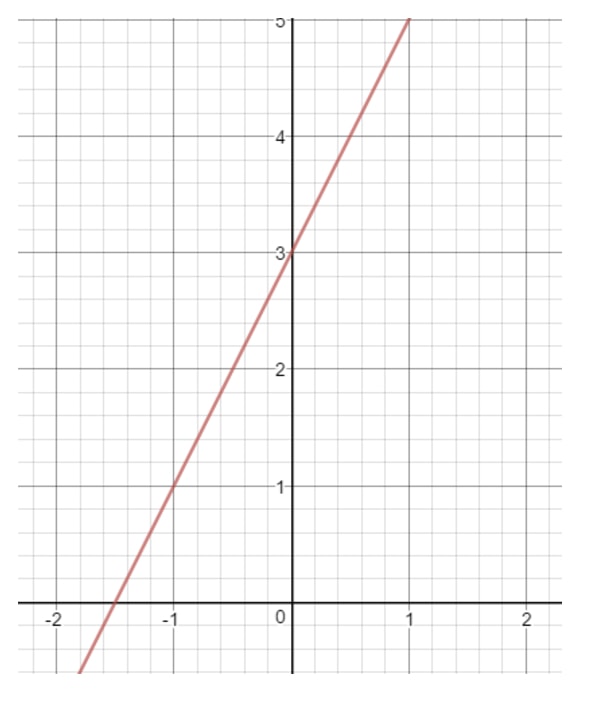
Om du tittar noga på y-axeln rör den raka linjen vid y-axeln på ett visst ställe. Var ligger den platsen? Det skulle vara siffran 3 eftersom det är där y-axeln och linjen skär varandra. Det betyder att vi kan dra slutsatsen att b = 3.

Vad är m i form av lutning och intercept?

Bokstaven m är ett tal som representerar linjens lutning. Vissa människor hänvisar till lutningen som stigande över löpning. Kom ihåg att om vi har två punkter kan vi hitta lutningen för de två punkterna genom att använda lutningsformeln

m=riserun=y2-y1x2-x1m = \frac{rise}{run} = \frac{y_{2} – y_{1}}}{x_{2} – x_{1}}}m=runrise=x2-x1y2-y1

Samma idé fungerar här. Om vi tar två valfria punkter på en rät linje kan vi hitta linjens lutning med hjälp av ovanstående formel! Låt oss till exempel använda den här linjen.

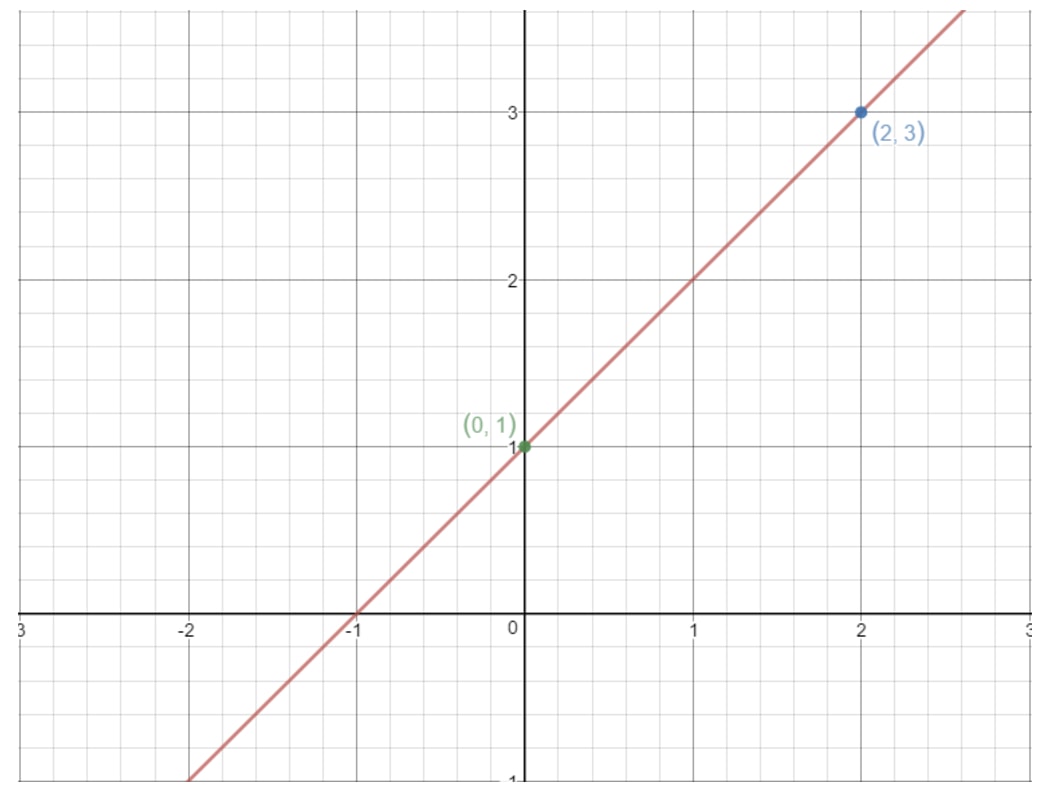
Märk att punkterna (2, 3) och (0, 1) ligger på den här grafen. Så varför använder vi inte dessa två punkter för att hitta linjens lutning? Med hjälp av formeln skulle vi få:

m=y2-y1x2-x1=1-30-2m = \frac{y_{2} – y_{1}}}{x_{2}} – x_{1}}} = \frac{1 – 3}{0 – 2}m=x2-x1y2-y2-y1=0-21-3=-2-2-2= \frac{-2}{-2}{-2}=-2-2-2=1= 1=1=1

Det betyder att lutningen på denna linje är 111!

Det speciella med lutningar är att vi kan använda två valfria punkter på linjen för att hitta den. Så om du tog två olika punkter på den här linjen skulle du fortfarande få fram att lutningen är 111.

Hur skriver man en ekvation i form av lutning och intercept?

Du kanske vet hur formen för lutning och intercept ser ut, men hälften av gångerna kommer du att få ekvationer som inte är i den formen. Så det är din uppgift att omvandla dem till lutningsavsnittsform. Hur gör vi det? Målet är att alltid isolera yyy-termen. Låt oss till exempel säga att du får ekvationen

6x+4+2y=06x + 4 + 2y = 06x+4+2y=0

För att isolera yyy, flyttar vi 6x+46x + 46x+4 till den högra sidan av ekvationen

2y=-6x-42y = -6x – 42y=-6x-4

Nu är 222 i vägen för yyy, så vi ska göra oss av med den genom att dividera båda sidor av ekvationen med 222.

2y2=-6x-42\frac{2y}{2} = \frac{-6x – 4}{2}22y=2-6x-4y=-6×2-42y = -\frac{6x}{2} – \frac{4}{2}y=-26x-24y=-3x-2y = -3x – 2y=-3x-2

Då yyy är isolerat kan man se att det är i form av lutning och intercept y=mx+by = mx + by=mx+b där m=-3m = -3m=-3, och b=-2b = -2b=-2.

Nu när vi känner till y-interceptet och lutningen riktigt bra, varför tittar vi inte på specifika frågor om att hitta dem!

Hur hittar man y intercept?

Fråga 1: Med hjälp av den linjära ekvationen y=12x+5y = \frac{1}{2} x + 5y=21x+5, hitta y intercept.

Bemärk här att ekvationen redan är i formen för lutning och intercept y=mx+by = mx + by=mx+b. Vi behöver bara ta reda på vad bbb är. Vi kan se att b=5b = 5b=5, så y-interceptet är 555.

Låt oss göra en något svårare fråga.

Fråga 2: Bestäm y-interceptet till 2x-4y=82x – 4y = 82x-4y=8

Nu är den här linjära ekvationen inte i form av lutning-interceptet, så vi måste ändra den till den formen först. Vårt mål är att isolera yyy i den här ekvationen.

Se att om vi flyttar 2x2x2x till den högra sidan av ekvationen får vi:

-4y=8-2x-4y = 8 – 2x-4y=8-2x

Nu dividerar vi båda sidorna med -4-4-4 och får:

-4y-4=8-2x-4\frac{-4y}{-4} = \frac{8 – 2x}{-4}-4-4-4y=-48-2xy=8-4-2x-4y = \frac{8}{-4} – \frac{2x}{-4}y=-48–42xy=-2+12xy = -2 + \frac{1}{2}xy=-2+21x

Nu byter vi positionerna för de två termerna och får:

y=12x-2y = \frac{1}{2}x – 2y=21x-2

Fråga 3: Bestäm y-interceptet till 4y-8=04y – 8 = 04y-8=0.

Detta kan se lite konstigt ut eftersom det inte finns någon xxx-term, men vårt mål förblir detsamma. Vi ska isolera yyy.

Om vi flyttar -8-8-8 till ekvationens högra sida får vi:

4y=84y = 84y=8

Dividerar vi båda sidorna av ekvationen med 444 får vi

4y4=84\frac{4y}{4} = \frac{8}{4}44y=48y=2y = 2y=2

Nu ser det kanske inte ut så här, men ekvationen är i form av en lutning-intercept. Det är bara det att m=0m = 0m=0, så hela termen mxmxmxmx har försvunnit. Skriv bara om ekvationen som

y=0m+2y = 0m + 2y=0m+2

Från att observera kan du se att b=2b = 2b=2, och så är y-interceptet 222. Vi gör en fråga till.

Fråga 4: Bestäm (om möjligt) y-interceptet till 5x-15=05x – 15 = 05x-15=0.

Denna fråga är intressant eftersom ekvationen inte har någon yyy-term. Så hur ska vi sätta den i form av lutningsintercept? Tja, det enda vi kan göra just nu är att isolera för xxx, så låt oss försöka med det för tillfället.

Om vi flyttar 151515 till ekvationens högra sida får vi:

5x=155x = 155x=15

Om vi dividerar båda sidor av ekvationen får vi:

5×5=155\frac{5x}{5} = \frac{15}{5}55x=515x=3x = 3x=3

Nu ska vi rita in detta i en graf. Lägg märke till att i den här ekvationen tvingas xxx vara 333 och kan inte vara något annat. Däremot står det inget om yyy, så yyy kan vara vad den vill. Om vi skulle skriva en värdetabell får vi:

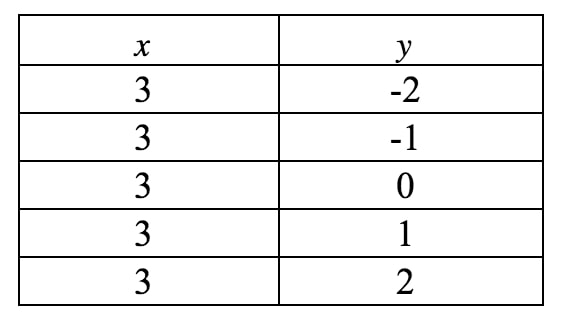
Om vi plottar dessa punkter på ett koordinatplan och drar linjen får vi:

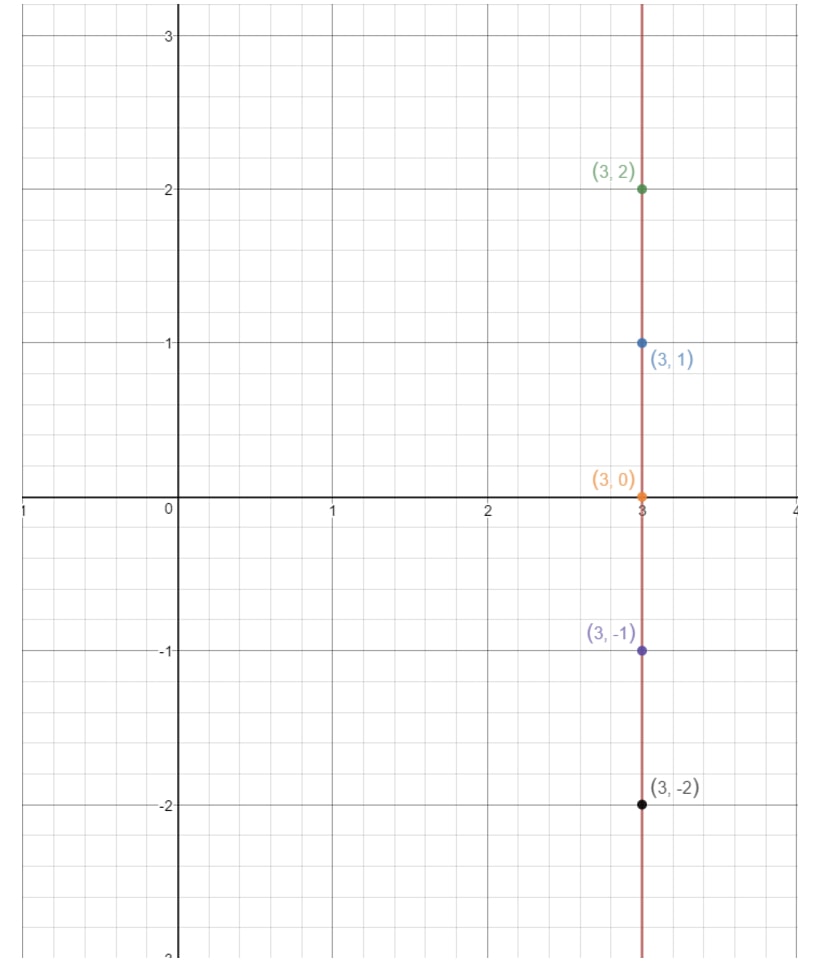
Bemärk hur linjen aldrig rör y-axeln. Det betyder att ekvationen inte har någon y-intercept. Nu när vi har täckt alla fall av att hitta y-interceptet, låt oss titta på frågor som ber oss att hitta lutningen!

Hur hittar man lutningen på en ekvation?

Fråga 5: Hitta lutningen till y=32x+1y = \frac{3}{2}x + 1y=23x+1

Fråga 6: Bestäm lutningen till den linjära ekvationen 6x-6y=06x – 6y = 06x-6y=0

Som du ser är ekvationen inte i form av lutningsintervallet, så vi måste först omvandla den till den formen. Vårt mål är att isolera yyy.

Om vi flyttar 6x6x6x till ekvationens högra sida får vi:

-6y=-6x-6y = -6x-6y=-6x

Dividerar vi båda sidorna med -6-6-6-6 får vi:

-6y-6=-6x-6\frac{-6y}{-6} = \frac{-6x}{-6}-6-6y=-6-6-6xy=xy = xy=x

Bemärk att detta egentligen är i form av lutning och intercept y=mx+by = mx + by=mx+b. Det är bara det att y-interceptet bbb i det här fallet är 000, och xxx är detsamma som 1x1x1x. Så vi kan skriva om ekvationen till:

y=1x+0y = 1x + 0y=1x+0

Nu ser vi genom att observera att m=1m = 1m=1. Eftersom mmm är lutningen måste lutningen vara 111. Låt oss göra en lite svårare

Fråga 7: Bestäm lutningen på 2y-4=02y – 4 = 02y-4=0

Även detta är lite konstigt eftersom vi inte har någon xxx-term. Vårt mål att isolera yyy förblir dock detsamma.

Om vi flyttar -4-4-4 till ekvationens högra sida får vi:

2y=42y = 42y=4

Dividerar vi båda sidor av ekvationen med 222 får vi:

2y2=42\frac{2y}{2} = \frac{4}{2}22y=24y=2y=2y = 2y=2

Se här att det nu är i form av lutning-intercept, förutom att termen mxmxmx är dold eftersom m=0m = 0m=0. Så vi kan skriva om vår ekvation som:

y=0x+2y = 0x + 2y=0x+2

Då m=0m = 0m=0, så har vi en noll lutning. Om du undrar hur en linje med 000 lutning ser ut, så finns här en graf som du kan se:

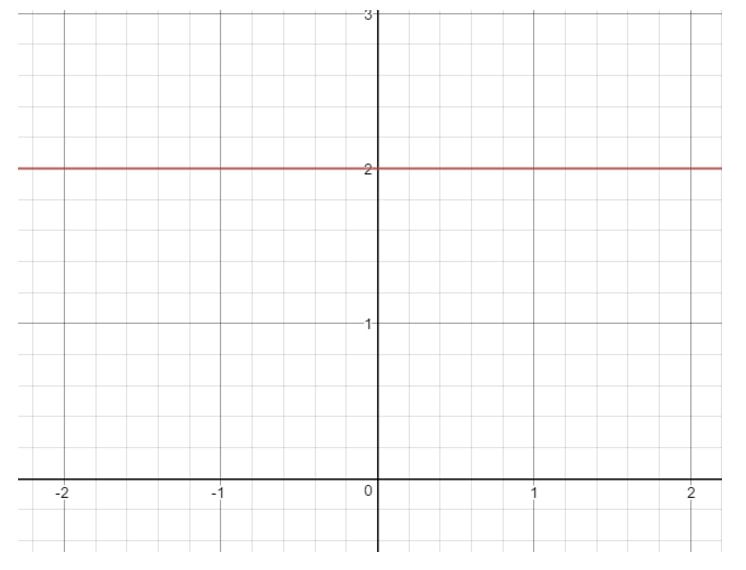
Fråga 8: Hitta (om möjligt) lutningen för den linjära ekvationen 16-4x=016 – 4x = 016-4x=0

I det här fallet kan yyy inte isoleras eftersom det inte finns någon yyy-term. Så det enda vi kan göra är att isolera xxx.

Om vi flyttar 161616 till ekvationens högra sida får vi:

-4x=-16-4x = -16-4x=-16

Om vi dividerar båda sidorna med -4-4-4 får vi:

-4x-4=-16-4\frac{-4x}{-4} = \frac{-16}{-4}-4-4-4x=-4-16x=4x = 4x=4

Detta är fortfarande inte i form av en lutning med intercept, så vårt enda hopp om att få fram lutningen är att rita en graf av denna linje. Återigen ser vi att xxx alltid tvingas vara 444, men yyy kan vara vad den vill eftersom det inte finns någon yyy-term. Om vi skulle skriva en värdetabell får vi:

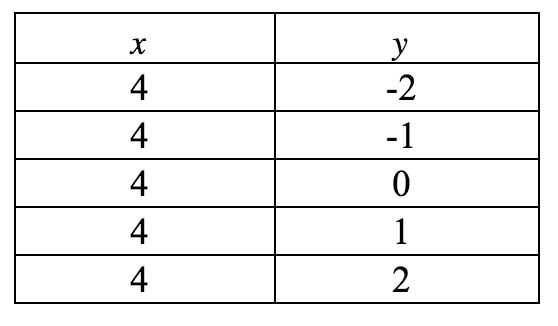
Om vi plottar dessa punkter på ett koordinatplan och ritar linjen får vi:

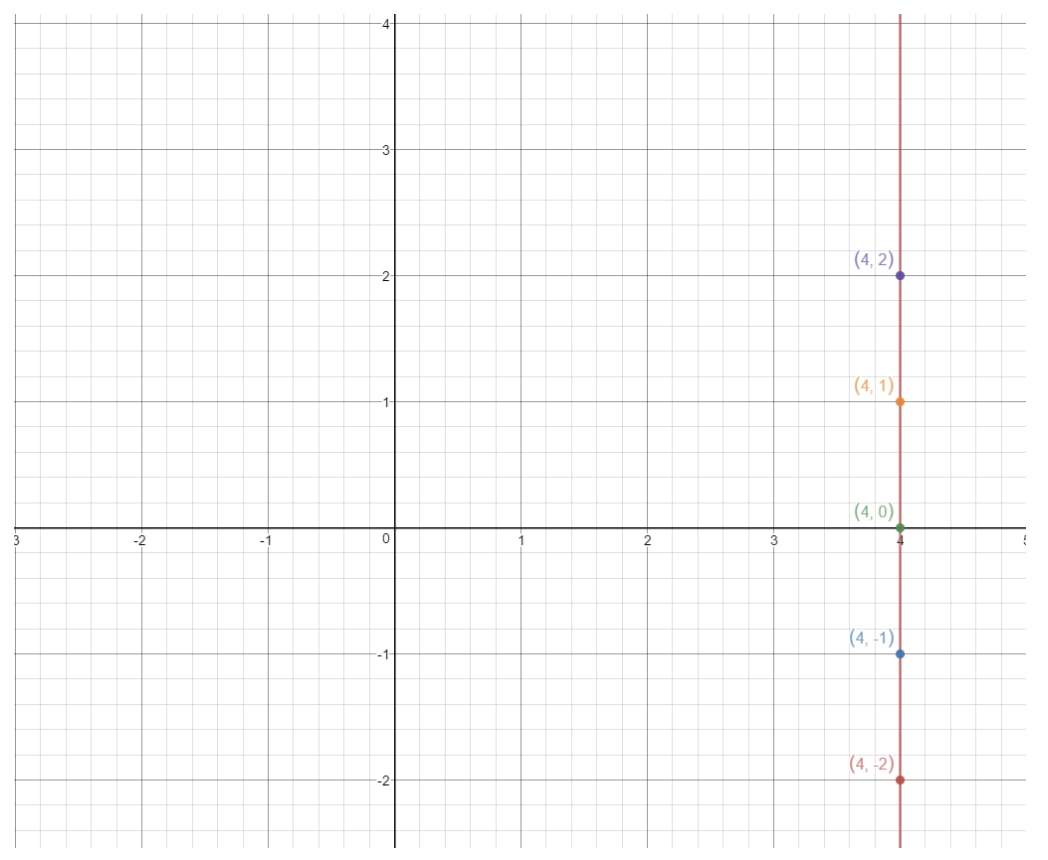
Detta är en vertikal linje. Vad är lutningen på en vertikal linje? Låt oss försöka ta reda på det genom att hitta stigningen och löpningen. Se hur den här linjen alltid stiger i all oändlighet, men det finns ingen löpning alls. Så det betyder att det finns en stigning på 000. Så om vi beräknar lutningen får vi:

m=riserun=rise0=undefinedm = \frac{rise}{run} = \frac{rise}{0} = undefinedm=runrise=0rise=undefined

Vi kan inte dividera med 000, så vi har faktiskt en odefinierad lutning.

Vad är en odefinierad lutning?

En odefinierad lutning är en lutning som går rakt uppåt i grafen. Som man ser i grafen ovan stiger lutningen oändligt och har ingen löpning. Som ett resultat får vi en odefinierad lutning eftersom vi inte kan dividera med 000.

I allmänhet får vi alltid en odefinierad lutning när vi får en rak vertikal linje!

Vi tittar på några andra unika frågor!

Finnande av ekvation från en punkt

Fråga 9: En punkt (2, 6) passerar genom en ekvation som är y=-5x+by = -5x + by=-5x+b. Hitta ”bbb”.

6=-5(2)+b6 = -5(2) + b6=-5(2)+b

Isolering och lösning av bbb ger:

6=-10+b6 = -10 + b6=-10+bb=16b = 16b=16

Håll dig i minnet att bbb också kallas y-snittpunkten, så y-snittpunkten är också 161616!

Finnande av lutning från två punkter

Fråga 10: Givet två punkter (6, 1) och (-10, 9), hitta linjens lutning.

Håll dig i minnet att för att hitta linjens lutning använder vi lutningsekvationen

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}}{x_{2} – x_{1}}}m=x2-x1y2-y1

Därmed ger denna formel oss:

m=9-1-10-6=8-16m = \frac{9 – 1}{-10 – 6} = \frac{8}{-16}m=-10-69-1=-168=1-2= \frac{1}{-2}=-21

Hur är det då om vi ska hitta hela ekvationen för en linje istället?

Ekvation för en linje givet två punkter

Fråga 11: Givet två punkter (-6, 1) och (2, 6), hitta ekvationen i form av lutningen interceptformen.

Vi försöker i princip hitta ekvationen i form av y=mx+by = mx + by=mx+b. För att göra detta måste vi leta efter mmm och bbb.

Håll dig i minnet att för att hitta mmm använder vi lutningsekvationen

m=y2-y1x2-x1m = \frac{y_{2} – y_{1}}}{x_{2} – x_{1}}}m=x2-x1y2-y1

Därmed ger denna formel oss:

m=6-12-(-6)=58m = \frac{6 – 1}{2 – (-6)} = \frac{5}{8}m=2-(-6)6-1=8558\frac{5}{8}85

Så nu har vi ekvationen

y=58x+by = \frac{5}{8}x + by=85x+b

Nu måste vi leta efter bbb. För att lösa bbb väljer vi någon av de givna punkterna och sätter in den i ekvationen. Det kan vi göra eftersom båda punkterna ligger på linjen, och alla punkter på linjen skulle uppfylla ekvationen. Låt oss använda punkten (2, 6). Se att:

6=58(2)+b6 = \frac{5}{8}(2) + b6=85(2)+b

Isolera bbb ger:

6=108+b6 = \frac{10}{8} + b6=810+bb=6-108b = 6 – \frac{10}{8}b=6-810b=488-108b = \frac{48}{8} – \frac{10}{8}b=848-810b=388b = \frac{38}{8}b=838

Omvandlar vi detta i decimalform får vi att b=4,75b = 4,75b=4,75. Därför är vår ekvation i form av lutning och intercept form:

y=58x+4,75y = \frac{5}{8}x + 4,75y=85x+4,75

Det sista som vi ska ta upp i det här avsnittet är att hitta linjens domän och område.

Hur hittar man domän och område?

För att hitta linjens domän ställer vi oss i princip den här frågan: Vad kan xxx vara? Om xxx kan vara dessa värden lägger vi till dem i domänen.

Det samma gäller för intervallet. Vad kan yyy vara? Om yyy kan vara dessa värden lägger vi till dem i intervallet. Låt oss ta ett exempel.

Fråga 12: Hitta domänen och området för ekvationen y=2x+1y = 2x + 1y=2x+1.

Observera att om vi ritar grafen för den här linjen får vi:

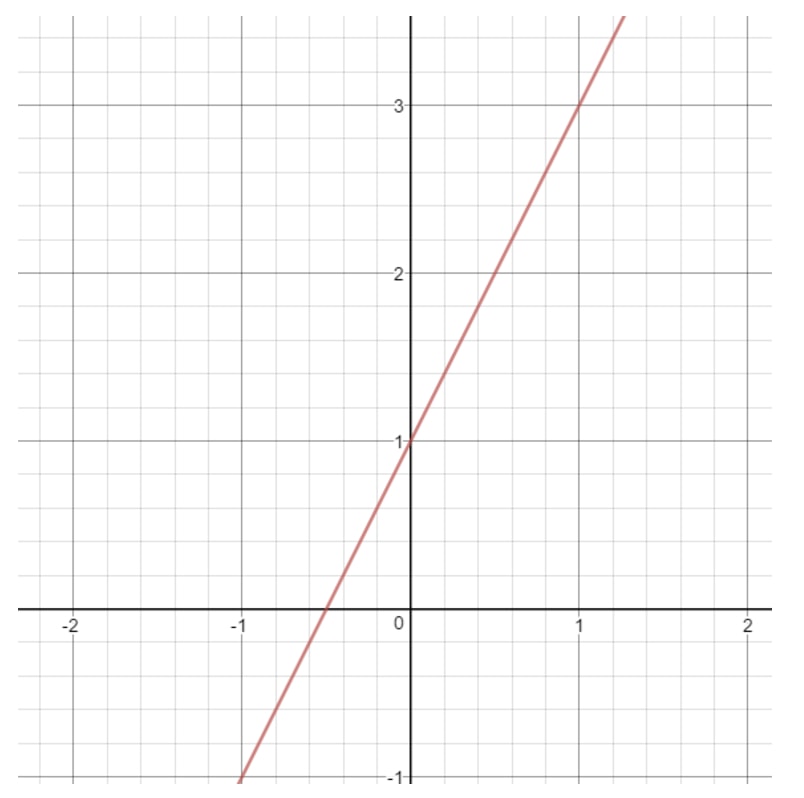
Vad kan xxx vara i den här linjen? Lägg märke till att xxx kan vara vad som helst eftersom vi med vilket xxx-värde som helst kan få en punkt som ligger på linjen. Samma sak gäller för y. Vi kan alltid välja ett yyy-värde som ger oss en punkt på en linje. Så vi säger att

Domän: {x∈\in∈R}Range: {y∈\in∈R}

där R betyder ”alla reella tal”. Låt oss göra en svårare fråga.

Fråga 13: Hitta domänen och området för ekvationen y=-2y = -2y=-2.

Om vi nu drar denna linje på en graf får vi:

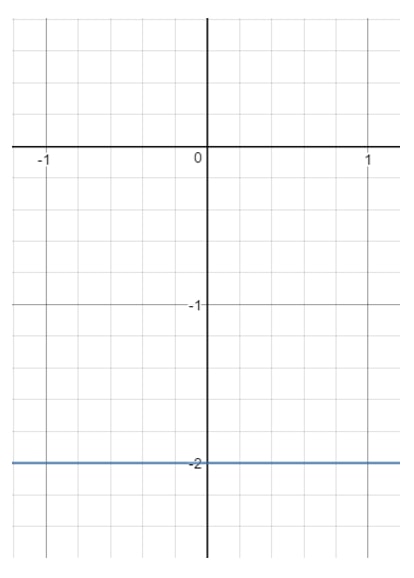
Bemärk att xxx kan vara vad som helst, för med vilket xxx-värde som helst kan vi få en punkt som ligger på linjen så länge y=-2y = -2y=-2. Men titta på yyy. Du ser att yyy är tvingad till -2-2-2-2 och kan inte vara något annat. I det ögonblick du väljer ett annat yyy-värde (t.ex. 111) kommer den punkten att ligga utanför linjen. Så det betyder:

Domän: {x ∈\in∈ R}Range: {y = -2}

Fråga 14: Hitta domänen och intervallet för ekvationen x=1x = 1x=1.

Om vi nu ritar upp denna linje på en graf får vi:

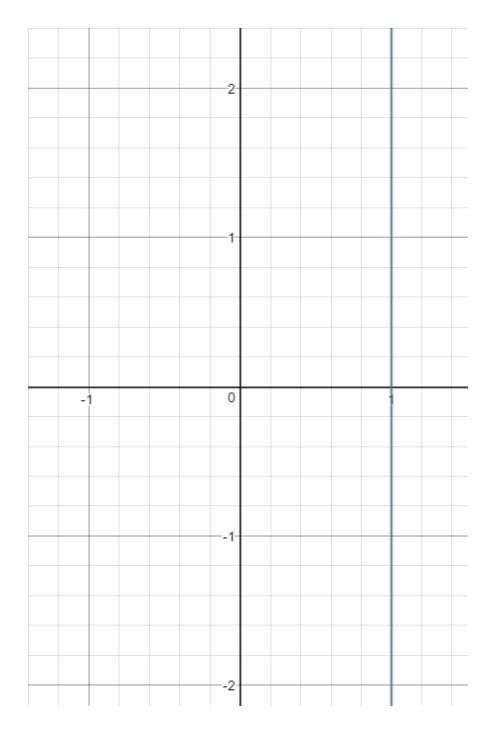
Du ser att xxx är tvingad att vara 111 och kan inte vara något annat. I det ögonblick du väljer ett annat xxx-värde (t.ex. 222) kommer den punkten att ligga utanför linjen.Titta dock på yyy. Lägg märke till att yyy kan vara vad som helst, för med vilket yyy-värde som helst kan vi få en punkt som ligger på linjen så länge x=1x = 1x=1

Så det betyder:

Domän: {x=1}Bredd: {

Om du hade mycket problem med att rita graferna för att få fram domänen och intervallet rekommenderar jag att du använder den här miniräknaren.

https://www.desmos.com/calculator/2rnqgoa6a4

Den lär dig hur man ritar en linjär ekvation. Allt du behöver göra är att skriva in värdena för mmm och bbb. Sedan ritar den automatiskt linjen åt dig! Detta är också användbart när du försöker hitta formeln för lutning-intercept.