Hur mycket vet du om oändligheter? Du har förmodligen hört talas om ett tal som är det största möjliga talet, eller omöjligt stort.

För att förklara oändligheter måste jag först definiera en del terminologi.

Integer är tal som används för att räkna. Mängden heltal definieras som alla tal utan bråkdelar. Några exempel är: Exempel: -12, 0, 1, 3, 42, 17.

Infinitet är begreppet ett objekt som ligger bortom de naturliga talens räckvidd. Det konceptualiserades först av en rysk matematiker vid namn Georg Cantor, som inte bara introducerade oändligheten utan också avslöjade att det fanns flera oändligheter som existerade.

Cantor gav ett kontroversiellt bevis för oändligheter, som sa att vissa oändligheter var större än andra. Till en början kan detta verka omöjligt – hur kan ett objekt vara större än ett annat objekt som är oändligt?

Cantor baserade sitt bevis på en gren av matematiken som till synes är värdelös: Mängdteori. En mängd är en samling objekt – till exempel kan vi ha en mängd som innehåller 1, 2 och 3. Dessa objekt i mängden kallas element.

I matematisk notation skulle detta se ut på följande sätt:

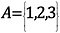
Antalet element i denna mängd, eller mängdens kardinalitet, är 3.

Detta betecknas som:

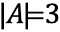
Om vi nu har en annan mängd, B, som innehåller objekt, så att

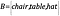
Hur vet vi att mängderna har samma storlek?

Ett sätt att se detta är att räkna antalet element i den andra mängden. Vi kan tydligt se att även denna mängd har 3 element i den, och därför vet vi att de har samma storlek.

Ett annat sätt att se detta är genom att jämföra vår andra mängd, B, med vår första mängd, A, genom mappning.

Vi kan mappa det första elementet från mängd A , 1, till det första elementet i mängd B, stol.

Vi kan mappa det andra elementet från mängd A, 2, till det andra elementet i mängd B, bord.

Vi kan mappa det tredje elementet från mängd A, 3, till det tredje elementet i mängd B, hatt.

Då varje element från A är mappat på exakt 1 element från B har mängderna samma storlek.

Låt oss nu ta en titt på oändliga mängder. Mängden helheter, som nämndes i början, är en oändlig mängd – det finns ett oändligt antal helheter. Mängden heltal betecknas med symbolen

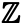
Mängden jämna tal, som vi kan beteckna som

definieras som

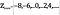
Intuitivt, kan det se ut som

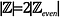
som det finns två heltal för varje jämnt heltal: 1 udda heltal och 1 jämnt heltal. Låt oss kontrollera detta.

Låt oss försöka jämföra mängderna genom att mappa element från 1 mängd till den andra.

Vi kan mappa 1 till 2, 2 till 4, 3 till 6 och så vidare.

Om detta fortsätter genom alla mängder kan vi se att varje element från heltalsmängden mappar på exakt ett element från den jämna heltalsmängden.

Därmed är mängderna lika stora, även om det kan tyckas vara kontraintuitivt.