Noll är ett tal som ligger rakt mellan de positiva och negativa talen på tallinjen. Noll betraktas som ett heltal tillsammans med de positiva naturliga talen (1, 2, 3, 4…) och de negativa talen (…-4,-3,-2,-1).

Noll är ett speciellt tal i heltalen eftersom det är det enda heltalet som varken är positivt eller negativt. Det är också det enda heltalet som varken är ett primtal eller ett sammansatt tal. Det anses vara ett jämnt tal eftersom det är delbart med 2 utan rest. Noll är det additiva identitetselementet i olika algebrasystem, och siffran ”0” används som ett platshållarvärde i positionella notationssystem för att representera tal.

Nollan har många intressanta egenskaper som gör att den är av intresse för matematiker. Om man adderar eller subtraherar noll från ett tal förblir talet detsamma Om man multiplicerar noll med ett tal blir resultatet noll. Alla tal som höjs till noll (0:e) potensen är 1, så 20=1 och 560=1. I traditionell algebra är division med 0 odefinierad, så inget tal kan divideras med 0. Talet 0 är också en del av de reella talen och de komplexa talen.

Historia om talet 0

Varifrån kom idén om noll? Numera verkar det intuitivt för oss; noll är ett tal som står för en nollkvantitet – ett ingenting. Vi ser nollor överallt i samhället, och vi förstår naturligtvis vad de betyder och hur de kan manipuleras matematiskt. Historiskt sett tog det dock ganska lång tid innan begreppet noll blev allmänt erkänt som ett objekt inom matematiken, och många genom historien hävdade att talet noll inte existerar, eller att idén noll är ett osammanhängande begrepp.

Många forntida samhällen hade inte något uttryckligt begrepp om kvantiteten noll eller en specifik siffra att använda för att representera den. De gamla egyptierna och babylonierna hade båda någon idé om en nollmängd och ett behov av platshållande värden i representationen av tal, men de utvecklade aldrig en särskild siffra eller ett särskilt begrepp för att representera denna mängd eller detta platshållande värde. De gamla egyptiska siffersystemen var helt och hållet bildliga och hade inga positionsvärden, medan de gamla babylonierna använde mellanslag mellan siffrorna för att representera positionsvärden.

Mayas hade ett uttryckligt begrepp 0 och hade en distinkt siffra för att representera begreppet och använda det som ett platshållarvärde i sitt vigesimala (bas-20) kalendersystem. Även om maya-samhällena, olmek-samhällena och andra förcolombianska samhällen var bland de första i historien som hade en uttalad och sofistikerad förståelse för talet 0, fortsatte dessa system inte att påverka den gamla världens samhällen i Europa.

De antika grekerna hade å andra sidan ett komplicerat förhållande till noll. De hade ingen symbol för dess begrepp eller för det som ett placeholdervärde eftersom de var osäkra på om talet 0 kunde betraktas som en genuint existerande sak. Hur, frågade de, kan något (ett tal) vara ingenting (noll)? För grekerna härrörde de naturliga talen (1, 2, 3, 4, …) från vår förståelse av diskreta individuella objekt i världen. Aristoteles själv hävdade som bekant att 0 inte existerar, med motiveringen att 0 representerar ett tomrum eller ingenting, och ett verkligt tomrum eller ingenting kan inte existera.

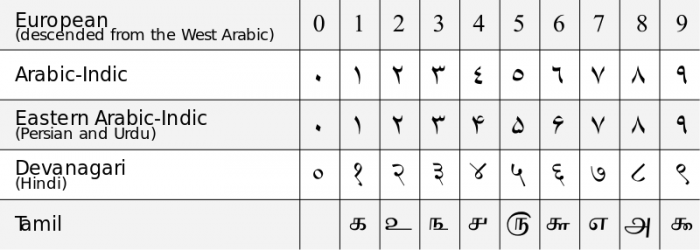
Kineserna hade en förståelse för ”0” som en platshållande siffra för sina räkneverk, men de ansåg inte att siffran ”0” representerade ett distinkt nummer, utan endast en användbar symbol. Den gemensamma förståelsen av 0 som ett distinkt tal och som en siffra för positionella notationssystem kom från Indien under 600-talet e.Kr. De indiska matematikerna vid den tiden utvecklade de första typerna av decimala (bas-10) notationssystem som innehöll 0 som en distinkt siffra och hade en förståelse för nollans unika matematiska egenskaper. På 1000-talet e.Kr. hade idén om nollan spridit sig till Västeuropa genom inflytande från islamiska matematiker som bodde i Spanien under Umayyadkalifatet, och det moderna arabiska numeriska systemet för decimalnotering skapades. Den första användningen av det engelska ordet ”zero” är från 1589.

Matematiska egenskaper hos noll

Talet noll spelar en viktig roll inom nästan alla matematiska områden. Noll är det minsta icke-negativa heltalet och har inget naturligt tal som föregår det. Eftersom 0 är ett heltal är det också ett rationellt tal, ett reellt tal och ett komplext tal. Inom matematiken anses 0 vara en kvantitet som motsvarar noll. Man kan säga att noll är den ”kvantitet” som besitter en mängd som inte har några medlemmar.

I algebra

I elementär algebra uttrycks noll ofta som att den ligger i mitten av tallinjen. Talet 0 anses vara ett jämnt tal eftersom det är en heltalsmultipel av talet 2 (2×0=0=0). 0 är inte ett primtal eftersom det har ett oändligt antal faktorer, och det är inte ett sammansatt tal eftersom ingen produkt av två primtal är lika med talet 0.

Med avseende på de fyra huvudsakliga aritmetiska operatörerna (+, -, ×, ÷) och exponentoperationen beter sig talet 0 enligt följande regler:

• Addition: x+0=0+x=x. Noll anses vara det additiva identitetselementet eftersom alla tal plus eller minus noll är lika med det talet
• Subtraktion: x-0=x och 0-x=-x
• Multiplikation: x⋅0=0=0⋅x=0. Alla tal gånger 0 är också lika med 0.
• Division: 0/x=0, utom när x=0. x/0 är en matematiskt odefinierad storhet, eftersom 0 inte har någon multiplikativ invers (inget tal gånger 0 ger 1).
• Exponenter: x0=1, utom när x=0. Det har länge diskuterats om 00 är odefinierat eller ett välformat uttryck. För alla positiva x gäller 0x=0.

I uttryck som involverar gränser kan kvantiteten 0/0 dyka upp i samband med att man ska visa gränser för rationella funktioner som f(x)/g(x). I dessa fall är 0/0 inte odefinierad utan representerar en obestämd form. Detta betyder inte att gränsen är odefinierad utan att den måste beräknas med hjälp av en annan metod, t.ex. genom att hitta derivata. Det finns vissa algebraiska modeller där division med noll ger en definierad kvantitet, till exempel den projektivt förlängda reella linjen eller Riemannsfären.

I mängdteori

I mängdteori motsvarar talet 0 kardinaliteten den ”tomma mängden” eller ”nollmängden” (vanligen representerad som {} eller {∅}. Kardinaliteten hos en mängd är antalet element i den mängden om man inte har några apelsiner, så har man en mängd med 0 apelsiner (en tom mängd apelsiner).

Zero används ofta som utgångspunkt i mängdteorin för att konstruera resten av de naturliga talen. Dessa von Neummankonstruktioner, uppkallade efter den berömde polymaten John von Neumann konstruerar de naturliga talen genom att definiera 0={} och definierar en efterföljande funktion S(a) = a ∪ {a}. Alla naturliga tal kan konstrueras genom rekursiva tillämpningar av efterföljarfunktionen med början i den tomma mängden:

0 = {}

1 = 0 ∪ {0} = {0} = {{}}

2 = 1 ∪ {1} = {0,1} = {{}, {{}}}

3 = 2 ∪ {2} = {0, 1, 2} = {{}, {{}}, {{}, {{}, {{}}}}

och så vidare. Genom att följa detta mönster kan man konstruera hela den oändliga mängden av de naturliga talen. På detta sätt kan man säga att varje naturligt tal motsvarar den mängd som innehåller alla de naturliga talen före det.

I fysiken

I samband med att man gör kvantitativa mätningar inom fysiken anses 0 vara den baslinje från vilken alla andra mätningar av enheter görs. Mycket ofta motsvarar baslinjen 0 någon fysikaliskt betydelsefull variabel som på ett naturligt sätt kan särskiljas från alla andra mätstorlekar.

I Kelvinskalan motsvarar till exempel en temperatur på 0 K absolut 0- den kallaste temperatur som är fysiskt möjlig. I Celsiusskalan definieras 0 °C som vattnets fryspunkt vid atmosfäriskt tryck. När det gäller dynamik och elektromagnetism ges värdet 0 till det läge där ett system har minsta möjliga mängd potentiell energi. Till exempel tilldelas en atoms grundtillstånd, den lägsta möjliga energinivån för atomens elektroner, ofta värdet 0.

Samma sak gäller för kinematik, där den referensram från vilken observationer av rörelser görs definieras som en referensram med en mittpunkt som ligger på koordinataxelns ursprung i punkten (0, 0). När det gäller bevarade storheter, som massa-energi, rörelsemängd och vinkelmoment, är den totala förändringen av bevarade storheter i ett isolerat system alltid lika med 0.

I datavetenskap

Datorer lagrar information i form av bitlånga sekvenser av 1:or och 0:or. I denna binära representation motsvarar 0 ett ”off”-läge och kontrasteras mot ”on”-läget som betecknas av 1. Ett värde på 0 i en elektrisk krets innebär att kretsen är avstängd och inte har något elektriskt flöde. På samma sätt definierar många beräkningslogiker ”0” som det tecken som representerar ett falskt sanningsvärde.

I datordatabaser räknas elementen i en matris med hjälp av ett nollbaserat räknesystem. Detta innebär att för en uppsättning med n element har elementen index som börjar med 0. Ett element med indextalet 0 är alltså i själva verket det första elementet i serien, och ett indextal på 1 motsvarar det andra elementet och så vidare. I allmänhet har den n:e termen i en serie ett indexnummer som motsvarar n-1. Detta räknesystem kan skapa förvirring hos nya programmerare som är vana vid att intuitivt tilldela indexvärden som börjar med 1.