Varianța este un număr care indică cât de departe se află un set de numere.Varianța este identică cu abaterea standard la pătrat și, prin urmare, exprimă „același lucru” (dar mai puternic).

Varianța – Exemplu

În cadrul unui studiu, 100 de persoane efectuează o sarcină simplă de viteză pe parcursul a 80 de încercări. Pentru fiecare participant, se înregistrează astfel 80 de timpi de reacție (în secunde). O parte din aceste date sunt prezentate mai jos.

În studii ca acestea, observăm de obicei că oamenii devin mai rapizi pe măsură ce execută sarcina de viteză mai des. Adică, timpul mediu de reacție tinde să scadă de-a lungul încercărilor.
De asemenea, timpii de reacție vor varia de obicei mai puțin între diferite persoane în măsura în care acestea efectuează sarcina mai des. Din punct de vedere tehnic, spunem că varianța scade de-a lungul încercărilor. Tabelul de mai jos ilustrează acest lucru pentru încercările 1,4,7 și 10.

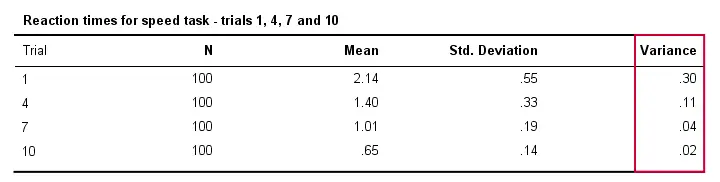
Varianță și histogramă

O modalitate excelentă de a vizualiza datele din tabelul nostru anterior este o histogramă pentru fiecare încercare. Astfel, figura de mai jos ilustrează faptul că participanții au devenit mai rapizi de-a lungul încercărilor; de la încercarea 1 la încercarea 10, barele histogramei se deplasează spre stânga, spre 0 secunde.

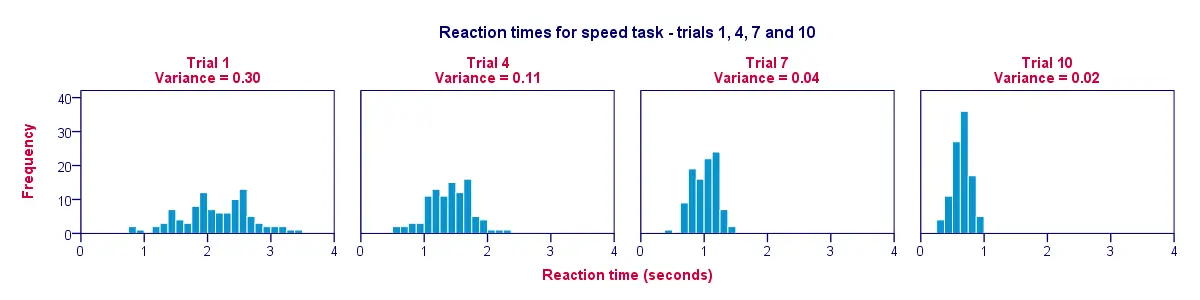
O a doua constatare este că histogramele devin mai înguste (și, prin urmare, mai înalte) pe măsură ce ne deplasăm de la încercarea 1 la încercarea 10; acest lucru ilustrează faptul că timpii de reacție variază din ce în ce mai puțin între participanții noștri pe măsură ce experimentul avansează. Varianța scade de-a lungul încercărilor.

Varianța – Formula populației

O formulă de bază pentru calcularea varianței este

$$S^2 = \frac{\sum(X – \overline{X})^2}{n}$$

Vă recomandăm să încercați să înțelegeți ce face această formulă, deoarece aceasta ajută foarte mult la înțelegerea ANOVA (= analiza varianței). Prin urmare, o vom demonstra pe o simplă mână de date.

Varianță – GoogleSheets

De dragul simplității, vom reduce datele noastre la prima încercare pentru primii 5 participanți. Acești 5 timpi de reacție -și un calcul manual al varianței lor- se află în această foaie de calcul GoogleSheet.

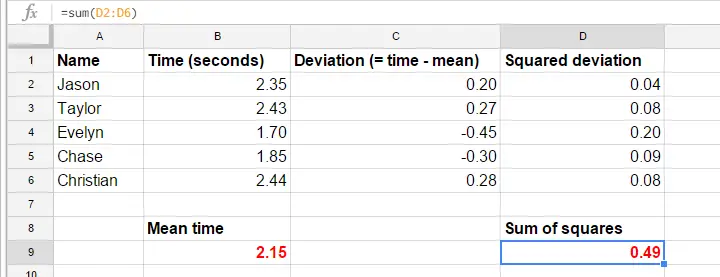
Varianță – Pași de calcul

Formulele din foaia de calcul GoogleSheet arată exact cum se calculează o varianță. Pașii de bază sunt

1. calculează timpul mediu de reacție (2,15);
2. calculează scorurile de abatere (timpul de reacție minus timpul mediu de reacție);
3. calculează scorurile de abatere la pătrat;
4. adăugă scorurile de abatere la pătrat. Rezultatul (0,49) este o sumă a pătratelor, principalul element constitutiv al ANOVA;
5. împărțiți suma pătratelor la numărul de observații (5 timpi de reacție).

Alternativ, calculați o varianță tastând =VARP(B2:B6) într-o celulă oarecare (B2:B6 sunt celulele care conțin cei 5 timpi de reacție ai noștri). VARP este prescurtarea pentru „varianța populației”. OpenOffice și MS Excel conțin formule similare.

Varianța – Formula eșantionului

În mod similar cu abaterea standard, dacă datele noastre sunt un simplu eșantion aleatoriu dintr-o populație mult mai mare, formula menționată mai sus va subestima sistematic varianța populației. În acest caz, vom folosi o formulă ușor diferită:

$$S^2 = \frac{\sum(X_i – \overline{X})^2}{n – 1}$$

Ce formulă să folosim depinde astfel de datele noastre: conțin ele întreaga populație pe care am dori să o investigăm sau sunt ele un simplu eșantion din această populație?
Din moment ce cei 100 de participanți ai noștri sunt în mod clar un eșantion, vom folosi formula eșantionului. În GoogleSheets, tastând =VAR(B2:B6) într-o celulă oarecare se va obține varianța eșantionului.

Varianța în SPSS

Din câte știm noi, formula pentru varianța populației este complet absentă din SPSS și considerăm că acesta este un defect grav. În schimb, SPSS utilizează întotdeauna formula de eșantionare. acest lucru este valabil atât pentru varianța între subiecți (discutată în acest tutorial), cât și pentru varianța în cadrul subiecților. Ieșirea relevantă este prezentată mai jos.

În ceea ce privește acest tabel de ieșire, rețineți, de asemenea, că varianța este într-adevăr abaterea standard la pătrat (în afară de rotunjire).

În ceea ce privește varianța, cam atât. Sperăm că ați găsit acest tutorial util pentru a înțelege ce este o varianță.

.