Statistică Definiții > Testul lui Friedman
Ce este testul lui Friedman?
Testul lui Friedman este un test neparametric pentru a găsi diferențe între tratamente în mai multe încercări. Neparametric înseamnă că testul nu presupune că datele dvs. provin dintr-o anumită distribuție (cum ar fi distribuția normală). Practic, este folosit în locul testului ANOVA atunci când nu cunoașteți distribuția datelor dumneavoastră.
Testul lui Friedman este o extensie a testului de semn, folosit atunci când există tratamente multiple. De fapt, dacă există doar două tratamente, cele două teste sunt identice.
Executarea testului
Datele dvs. trebuie să îndeplinească următoarele cerințe:
- Datele trebuie să fie ordinale (de ex. scara Likert) sau continue,
- Datele provin de la un singur grup, măsurate în cel puțin trei ocazii diferite,
- Eșantionul a fost creat cu o metodă de eșantionare aleatorie,
- Blocurile sunt independente între ele (i.e.adică toate perechile sunt independente – una nu o afectează pe cealaltă),
- Observațiile sunt ordonate în cadrul blocurilor fără egalități.
Ipoteza nulă pentru test este că toate tratamentele au efecte identice sau că eșantioanele diferă în vreun fel. De exemplu, acestea au centre, răspândiri sau forme diferite. Ipoteza alternativă este că tratamentele au într-adevăr efecte diferite.
Pregătiți datele pentru test.
Pasul 1: Sortați datele în blocuri (coloane într-o foaie de calcul).pentru acest exemplu, avem 12 pacienți care primesc trei tratamente diferite.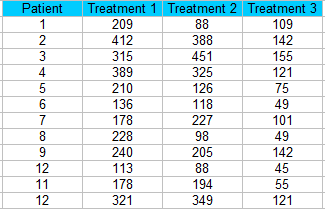
Pasul 2: Clasificați fiecare coloană separat. Cel mai mic scor ar trebui să primească un rang de 1. Aici fac un clasament pe rânduri, astfel încât fiecare pacient este clasat cu 1, 2 sau 3 pentru fiecare tratament.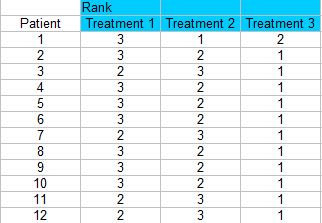
Pasul 3: Adunați rangurile (găsiți un total pentru fiecare coloană).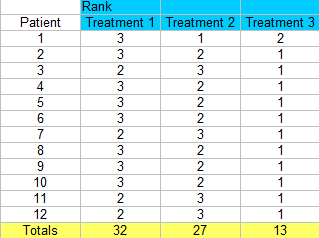
Executarea testului
Nota: Acest test nu este de obicei executat manual, deoarece calculele necesită mult timp și multă muncă. Aproape toate pachetele software statistice populare pot rula acest test. Cu toate acestea, includ aici pașii manual pentru referință.
Pasul 4: Calculați statistica testului. Veți avea nevoie de:
- n: numărul de subiecți (12)
- k: numărul de tratamente (3)
- R: Rangurile totale pentru fiecare dintre cele trei coloane (32, 27, 13).
Introduceți acestea în următoarea formulă și rezolvați: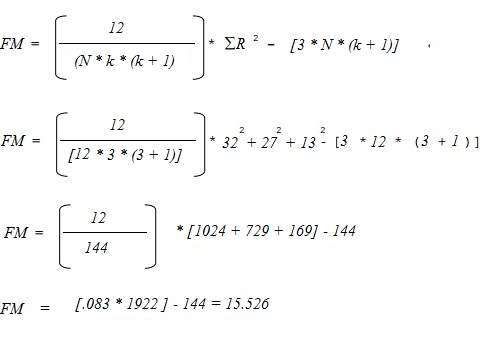
Pasul 5: Găsiți valoarea critică FM din tabelul de valori critice pentru Friedman (vezi tabelul de mai jos).
Utilizați tabelul k=3 (deoarece acesta este numărul de tratamente pe care îl avem) și un nivel alfa de 5%. Ați putea alege un nivel alfa mai mare sau mai mic, dar 5% este destul de comun – așa că folosiți tabelul cu 5% dacă nu cunoașteți nivelul alfa.
Cercând n-12 în acel tabel, găsim o valoare critică FM de 6,17.
Pasul 6: Comparați statistica de test FM calculată (Pasul 4) cu valoarea critică FM (Pasul 5). Respingeți ipoteza nulă dacă valoarea F calculată este mai mare decât valoarea critică FM.:
- Statistică de test FM calculată = 15,526.
- Valoare critică FM din tabel = 6,17.
Statistica FM calculată este mai mare, deci veți respinge ipoteza nulă.
Friedman’s ANOVA by Ranks Critical Value Table
Trei tabele în funcție de „k”.
Dacă k este mai mare de 5 sau n este mai mare de 13, folosiți tabelul valorii critice chi pătrat de la pasul 5 pentru a obține valoarea critică.
k=3
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 6.00 | 6.00 | – |
| 4 | 6.00 | 6.50 | 8.00 |
| 5 | 5.20 | 6.40 | 8.40 |
| 6 | 5.33 | 7.00 | 9.00 |
| 7 | 5.43 | 7.14 | 8.86 |
| 8 | 5.25 | 6.25 | 9.00 |
| 9 | 5.56 | 6.22 | 8.67 |
| 10 | 5.00 | 6.20 | 9.60 |
| 11 | 4.91 | 6.54 | 8.91 |
| 12 | 5.17 | 6.17 | 8.67 |
| 13 | 4.77 | 6.00 | 9.39 |
| ∞ | 4.61 | 5.99 | 9.21 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 2 | 6.00 | 6.00 | – |
| 3 | 6.60 | 7.40 | 8.60 |
| 4 | 6.30 | 7.80 | 9.60 |
| 5 | 6.36 | 7.80 | 9.96 |
| 6 | 6.40 | 7.60 | 10.00 |
| 7 | 6.26 | 7.80 | 10.37 |
| 8 | 6.30 | 7.50 | 10.35 |
| ∞ | 6.25 | 7.82 | 11.34 |
k=4
| N | α <.10 | α ≤.05 | α <.01 |
| 3 | 7.47 | 8.53 | 10.13 | 4 | 7.60 | 8.80 | 11.00 | 5 | 7.68 | 8.96 | 11.52 | ∞ | 7.78 | 9.49 | 13.28 |
Referință:
Analiză de varianță în două direcții a lui Friedman prin ranguri – Analiza datelor k-în-grup cu o
variabilă de răspuns cantitativ. Retrieved 7-17-2016 from: http://psych.unl.edu/psycrs/handcomp/hcfried.PDF
Stephanie Glen. „Friedman’s Test / Two Way Analysis of Variance by Ranks” From StatisticsHowTo.com: Statistică elementară pentru noi toți ceilalți! https://www.statisticshowto.com/friedmans-test/
——————————————————————————
Nevoie de ajutor cu o temă pentru acasă sau o întrebare de test? Cu Chegg Study, puteți obține soluții pas cu pas la întrebările dvs. de la un expert în domeniu. Primele 30 de minute cu un tutore Chegg sunt gratuite!