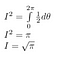Lord Kelvin a scris despre această integrală: „Un matematician este acela pentru care acest lucru este la fel de evident ca și faptul că de două ori doi fac patru pentru tine.”
Distracție plăcută 😉
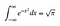
OK, deci voi presupune că știi câteva noțiuni de bază de integrare și diferențiere. Ceea ce urmează va adăuga ceva intuiție la trucurile inteligente care vor veni mai târziu. Nu vă faceți griji dacă unele dintre ele sunt ușor derutante, încercați doar să vă faceți o idee despre ce se întâmplă.
Strategia de aici va fi de a face o substituție inteligentă. Dar vom face o substituție în două variabile. Puteți vizualiza problema actuală ca fiind calcularea ariei sub o curbă
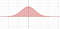
Dar vom arăta că problema poate fi transformată în una de calcul al unui volum.
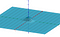
Pentru a calcula volumul, folosim o formulă de schimbare de variabilă ușor diferită de cea pe care o folosim în integralele normale. Vom folosi coordonate polare. Aceasta exprimă coordonatele x și y în termeni de rază și unghi. Geogebra are un mod interactiv frumos de a vedea acest lucru aici

Apoi vom folosi formula magică de schimbare a bazei pentru coordonate polare.
Când am calculat aria sub curbă, am avut elementul ‘dx’ care reprezintă o mică distanță de-a lungul axei x. Atunci când calculăm un volum, avem dx dy, care este ca un mic dreptunghi cu lungimea laturilor dx și dy. Apoi folosim aceste baze pentru a crea o serie de cutii care estimează volumul. Acest lucru este cel mai ușor de văzut cu ajutorul vizualizării de mai jos. Integrala este limita acestor aproximări.
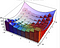
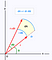
Când, în schimb, folosim sistemul de coordonate polare, avem dedesubt un element de suprafață ușor diferit. Mai jos, dA este elementul de arie. Cu mici modificări ale unghiului și ale razei, acest element de arie poate fi din ce în ce mai bine aproximat de un dreptunghi cu lungimile laturilor dr și, respectiv, r*dtheta. Dacă vă descurcați cu ceva geometrie, pentru theta mic sin(theta) este aproximat foarte bine de theta și puteți demonstra apoi rezultatul de mai jos.
Soluționarea integralei
În primul rând dăm un nume integralei noastre. O numim I.
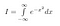
Rețineți că x este doar o „variabilă fictivă”. Zona există indiferent de numele variabilei pe care o folosim. Așadar, putem scrie și următoarele două ecuații
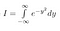
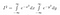
Acum, deoarece I este doar o constantă, deși una a cărei valoare nu o cunoaștem încă, putem folosi regulile noastre normale pentru aducerea unei constante în interiorul unei integrale
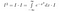
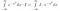
Până acum nu am făcut prea multe lucruri substanțiale. Acum ne gândim bine la ce înseamnă integrala. Luăm integrale de funcții. Dacă două funcții iau pretutindeni aceeași valoare, ele sunt identice și au aceeași arie. Ținând cont de asta, putem face următoarele manipulări, dacă privim I*exp(-x²) ca pe o funcție a lui x, adică ceva care primește valori ale lui x ca intrare și dă un număr ca ieșire.
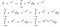
Ok, asta a fost mult de asimilat. În prima linie, am rescris pur și simplu I în forma sa integrală cu un nume de variabilă diferit. În al doilea rând, tratând I*exp(-x²) ca pe o funcție, ne-am dat seama că putem aduce exp(-x²) în interiorul integralei dy, iar acest lucru ar da în continuare aceeași valoare de ieșire pentru orice valoare de intrare a lui x. În cele din urmă, am folosit regulile de exponențiere.
Scriind acest lucru în întregime, avem acum
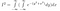
În continuare vine intuiția ucigașă. Mai sus ne-am încurcat cu numele variabilelor și cu modul de reprezentare a unei funcții. Acum ne schimbăm perspectiva: această expresie reprezintă, de asemenea, integrala lui exp(-(y²+x²)) pe întregul plan 2D, cu elementul de arie dA = dx dy. Adică dx dy este un mic dreptunghi pe un plan, iar exp(-(-(y²+x²)) este înălțimea deasupra acelui dreptunghi.
În continuare, folosim cunoștințele de coordonate polare de mai devreme
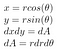
Ca sin² + cos² = 1, după ce am băgat totul în calcul, obținem
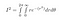
r variază de la 0 la infinit, iar theta variază de la 0 la 2*pi, deoarece aceasta acoperă întregul plan 2D: orice punct are o rază mai mică decât infinitul și un unghi cuprins între 0 și 2pi radiani.
Putem evalua integrala interioară folosind regula lanțului
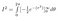
Și, în țara promisă ne aflăm acum: