Evenimentele aleatoare care au loc într-un spațiu continuu de eșantionare pot invoca imagini geometrice din cel puțin două motive: din cauza naturii problemei sau din cauza naturii soluției.

Câteva probleme, cum ar fi acul lui Buffon, Păsările pe sârmă, Paradoxul lui Bertrand sau problema bățului rupt în trei bucăți apar, prin natura lor, într-un cadru geometric. Aceasta din urmă admite, de asemenea, multiple reformulări care necesită compararea ariilor unor figuri geometrice. În general, ne putem gândi la probabilitățile geometrice ca la niște cantități nenegative (care nu depășesc 1) care sunt atribuite unor subregiuni ale unui domeniu dat, sub rezerva anumitor reguli. Dacă funcția μ este o expresie a acestei atribuiri definită pe un domeniu D, atunci, de exemplu, avem nevoie de

0 ≤ μ(A) ≤ 1, A ⊂ D și
μ(D) = 1

Funcția μ nu este de obicei definită pentru toate A ⊂ D. Acele subansamble din D pentru care μ este definită sunt evenimentele aleatoare care formează un anumit spațiu de eșantionare. Foarte adesea, μ este definită prin intermediul raportului dintre arii, astfel încât, dacă σ(A) este definită ca „aria” ansamblului A, atunci se poate stabili μ(A) = σ(A) / σ(D).

Problema 1

Doi prieteni care iau metroul pentru a merge la locul de muncă din aceeași stație ajung la stație în mod uniform și aleatoriu între 7 și 7:20 dimineața. Ei sunt dispuși să se aștepte unul pe celălalt timp de 5 minute, după care iau un tren fie împreună, fie singuri. Care este probabilitatea ca ei să se întâlnească în stație?

Într-un sistem cartezian de coordonate (s, t), un pătrat de latură 20 (minute) reprezintă toate posibilitățile de sosire dimineața a celor doi prieteni în stația de metrou.

Zona gri A este delimitată de două drepte, t = s + 5 și t = s – 5, astfel încât în interiorul lui A, |s – t| ≤ 5. Rezultă că cei doi prieteni se vor întâlni numai cu condiția ca s și t să cadă în regiunea A. Probabilitatea ca acest lucru să se întâmple este dată de raportul dintre aria lui A și aria pătratului:

/ 400 = 175/400 = 7/16.

Problema 2

(.)

Trei puncte A, B, C sunt plasate la întâmplare pe un cerc de rază 1. Care este probabilitatea ca ΔABC să fie acut?”

Fixați punctul C. Pozițiile punctelor A și B sunt atunci definite de arcele α și β care se extind din C în două direcții. A priori știm că 0 < α + β < 2π. Valorile favorabile pentru problema noastră ale lui α și β (ca unghiuri acute subtendente satisfac) 0 < α < π și 0 < β < π. Suma lor nu poate fi mai mică decât π, deoarece aceasta ar face ca unghiul C să fie obtuz, deci, α + β > π. Situația este prezentată în următoarea diagramă în care pătratul are latura 2π.

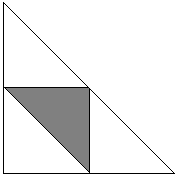
Regunea D este intersecția a trei semiplane: 0 < α, 0 < β și α + β < 2π. Acesta este triunghiul mare din diagrama de mai sus. Evenimentele favorabile aparțin triunghiului umbrit, care este intersecția semiplanurilor α < π, β < π și α + β > π. Raportul dintre ariile celor două este, evident, 1/4.

Observați acum că, dacă triunghiul oarecare nu este acut, el poate fi considerat drept obtuz, deoarece probabilitatea ca două dintre cele trei puncte A, B, C să formeze un diametru este 0. (Pentru ca BC să fie un diametru, ar trebui să avem α + β = π, care este o dreaptă, cu zero ca singură atribuire posibilă a ariei). Astfel, putem spune că probabilitatea ca ΔABC să fie obtuz este de 3/4. Pentru un triunghi obtuz, cercul poate fi împărțit în două jumătăți, triunghiul aflându-se în întregime într-una din jumătăți. Rezultă că 3/4 este răspunsul la următoarea întrebare:

Trei puncte A, B, C sunt plasate la întâmplare pe un cerc de rază 1. Care este probabilitatea ca toate trei să se afle într-un semicerc?

1. E. J. Barbeau, Murray S. Klamkin, W. O. J. Moser, Cinci sute de provocări matematice de: (MAA, 1995, problema 244.)
2. D. A. Klain, G.-C. Rota Introduction to Geometric Probability , Cambridge University Press, 1997
3. A. A. Sveshnikov, Problems in Probability Theory, Mathematical Statistics and Theory of Random Functions, Dover, 1978
4. A. M. Yaglom, I. M. Yaglom, Challenging Mathematical Problems With Elementary Solutions, Dover, 1987

Geometric Probability

• Geometric Probabilities
• Are Most Triangles Obtuse?
  • Opt selecții în șase sectoare
  • Trei puncte aleatoare pe un cerc
• Probabilitate geometrică
  • Stick rupt în trei bucăți (coordonate triliniare)
  • Stick rupt în trei bucăți. Soluție în coordonate carteziene
• Paradoxul lui Bertrand
• Păsări pe sârmă (Problemă și simulare interactivă)
  • Păsări pe sârmă: Soluție de Nathan Bowler
  • Birds on a Wire. Soluție de Mark Huber
  • Birds on a Wire: o simulare probabilistică. Soluție de Moshe Eliner
  • Birds on a Wire. Soluție de Stuart Anderson
  • Birds on a Wire. Soluție de Bogdan Lataianu
• Buffon’s Noodle Simulation
• Averaging Raindrops – an exercise in geometric probability
  • Averaging Raindrops, Part 2
• Rectangle on a Chessboard: o introducere
• Marcarea și ruperea bețelor
• Puncte aleatorii pe un segment
• Acoperirea unui semicerc
• Acoperirea unei semisfere
• Acoperirea unei semisfere
• Intervale aleatoare suprapuse
• Intervale aleatoare cu o dominantă
• Puncte pe o grilă pătrată
• Probabilități plane pe o sferă
• Probabilitate în triunghi

|Contact|||Prima pagină|||Contenit|||În sus|

Copyright © 1996-2018 Alexander Bogomolny

.